Toptailieu.vn biên soạn và giới thiệu Lý thuyết Ôn tập chương 1 (Kết nối tri thức) Toán 7 hay, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững nội dung kiến thức từ đó dễ dàng làm các bài tập Toán 7.

Lý thuyết Ôn tập chương 1 (Kết nối tri thức) Toán 7

A. Lý thuyết

1. Khái niệm số hữu tỉ và biểu diễn số hữu tỉ trên trục số

• Số hữu tỉ là số viết được dưới dạng phân số ab với a, b ∈ ℤ, b ≠ 0.

Tập hợp các số hữu tỉ được kí hiệu là ℚ.

• Cách biểu diễn số hữu tỉ ab trên trục số:

 + Chia đoạn thẳng đơn vị thành b phần bằng nhau, lấy một đoạn làm đơn vị mới.

 + Điểm biểu diễn số hữu tỉ ab cách O một đoạn bằng a đơn vị mới và nằm trước O (nếu số hữu tỉ âm) hoặc nằm sau O (nếu số hữu tỉ dương).

Ví dụ 1:

+  Các số – 7; 0,3; – 234 là các số hữu tỉ vì chúng viết được dưới dạng phân số: – 7 = −71; 0,3 = 310; – 234 = −114.

+ Biểu diễn số hữu tỉ 32 trên trục số ta làm như sau:

Chia đoạn thẳng đơn vị thành 2 phần bằng nhau. Lấy một đoạn làm đơn vị mới (H.a).

Số hữu tỉ 32 được biểu diễn bởi điểm N (nằm sau gốc O) và cách O một đoạn bằng 3 đơn vị mới (H.b)

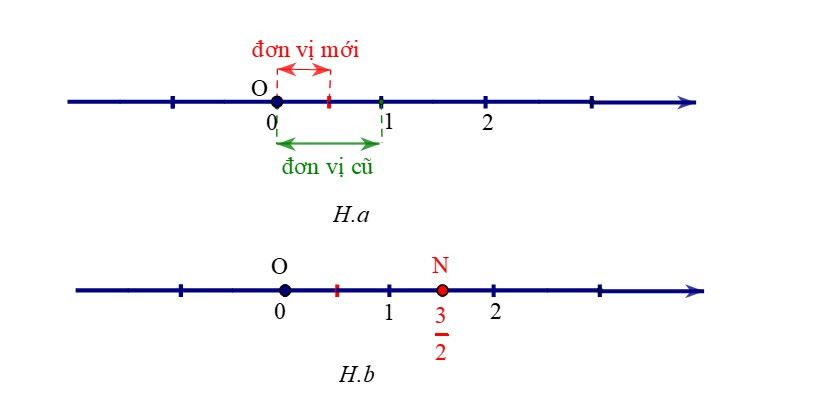
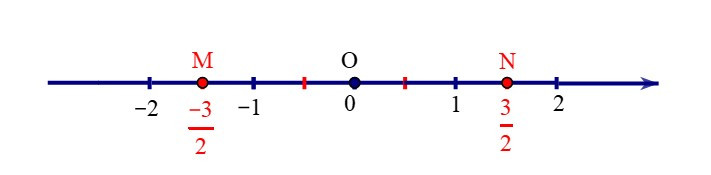
+ Số đối của số hữu tỉ 32 là số hữu tỉ −32 được biểu diễn bởi điểm M (nằm trước gốc O). Ta có OM = ON.

Chú ý:

• Mỗi số hữu tỉ đều có một số đối. Số đối của số hữu tỉ m là số hữu tỉ – m.

• Số thập phân có thể viết dưới dạng phân số thập phân nên chúng đều là các số hữu tỉ. Tương tự, số nguyên, hỗn số cũng là các số hữu tỉ.

• Trên trục số, hai điểm biểu diễn của hai số hữu tỉ đối nhau nằm về hai phía khác nhau so với điểm O và có cùng khoảng cách đến O.

Ví dụ 2: Số đối của các số hữu tỉ sau: −9,7;  358;  −12; 6.

Hướng dẫn giải

Số đối của 0 – 9,7 là – (– 9,7) = 9,7;

Số đối của  358 là  −358;

Số đối của −12 là −(−12)=12;

Số đối của 6 là  – 6.

2. Thứ tự trong tập hợp các số hữu tỉ

• Ta có thể so sánh hai số hữu tỉ bất kì bằng cách viết chúng dưới dạng phân số rồi so sánh hai phân số đó.

• Với hai số hữu tỉ a, b bất kì, ta luôn có hoặc a = b hoặc a < b hoặc a > b.

Cho ba số hữu tỉ a, b, c. Nếu a < b và b < c thì a < c (tính chất bắc cầu).

• Trên trục số, nếu a < b thì điểm a nằm trước điểm b.

Ví dụ:

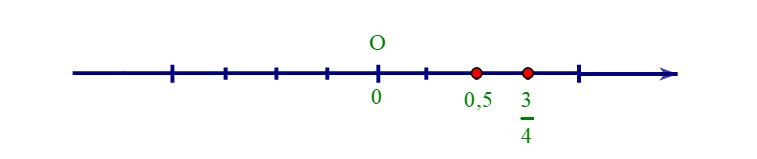
+ So sánh 0,5 và 34 ta làm như sau:

Ta có 0,5 = 510=12=24  

Vì 2 < 3 nên 24 < 34 hay 0,5 < 34.

+ 0,5 < 34 nên 0,5 nằm trước 34 trên trục số.

+ Ta có thể cử dụng tính chất bắc cầu để so sánh hai số hữu tỉ 56 và 65 như sau:

Vì 56<66=1 và 1=55<65 nên 56 < 1 < 65.

Vậy 56<65.

Chú ý:

• Trên trục số, các điểm nằm trước gốc O biểu diễn số hữu tỉ âm (tức số hữu tỉ nhỏ hơn 0); các điểm nằm sau gốc O biểu diễn số hữu tỉ dương (tức số hữu tỉ lớn hơn 0). Số 0 không là số hữu tỉ dương, cũng không là số hữu tỉ âm.

3. Cộng và trừ hai số hữu tỉ

Mọi số hữu tỉ đều viết được dưới dạng phân số với mẫu dương nên ta có thể cộng, trừ hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc cộng, trừ phân số.

Ví dụ 1: Tính:

a) −618+1827;

b) – 0,32 + 0,98;

c) – 5 + 215.

Hướng dẫn giải

a) −618+1827=−13+23=−1+23=13;

b) – 0,32 + 0,98 = 0,98 – 0,32 = 0,66;

c) – 5 + 215 = −255+115=−25+115=−145.

Chú ý:

• Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta có thể áp dụng quy tắc cộng và trừ đối với số thập phân.

• Trong phép cộng trừ với số hữu tỉ ℚ, ta có thể áp dụng các tính chất giao hoán, kết hợp, quy tắc dấu ngoặc như trong phép cộng trừ với số nguyên ℤ.

• Đối với một tổng trong ℚ, ta có thể đổi chỗ các số hạng, đặt dấu ngoặc để nhóm các số hạng một cách tùy ý như các tổng trong ℤ.

• Hai số đối nhau luôn có tổng bằng 0:

a + (– a) = 0.

Ví dụ 2: Thực hiện phép tính

a) 2−3+−56+13+116;

b) 313−12−(23−12).

Hướng dẫn giải

a) 2−3+−56+13+116

=−23+−56+13+76             (Viết số hữu tỉ dưới dạng phân số có mẫu dương)

=−23+13+−56+76             (Tính chất giao hoán)

=(−23+13)+(−56+76)      (Tính chất kết hợp)

=−13+26

=−13+13=0                       (Tổng hai số đối nhau bằng 0)

b)  313−12−(23−12)

=313−12−23+12                    (Quy tắc bỏ dấu ngoặc có dấu “–” đằng trước)

=(313−23)+(−12+12)         (Quy tắc đặt dấu ngoặc có dấu “+” đằng trước)

=293+0=293                       (Cộng với số 0)

4. Nhân và chia hai số hữu tỉ

• Ta có thể nhân, chia hai số hữu tỉ bằng cách viết chúng dưới dạng phân số rồi áp dụng quy tắc nhân, chia phân số.

Chú ý:

• Phép nhân các số hữu tỉ cũng có các tính chất của phép nhân phân số.

• Nếu hai số hữu tỉ đều được cho dưới dạng số thập phân thì ta có thể áp dụng quy tắc nhân và chia đối với số thập phân.

Ví dụ 1: Tính:

a) 233⋅646⋅(−910);

b) −76:157;

c) 76⋅314+76⋅(−0,25).

Hướng dẫn giải

a) 233⋅646⋅(−910)

=233⋅323⋅(−910)

=1⋅(−910)=−910                (Nhân với số 1)

b) −76:157

=−76:127

=−76⋅712=−4972

c) 76⋅314+76⋅(−0,25)

=76⋅[314+(−0,25)]

=76⋅(134+−14)

=76⋅124=72

Ví dụ 2: 1,25 . (– 4,6) = – (1,25 . 4,6) = – 5,75.

5. Lũy thừa với số mũ tự nhiên

• Lũy thừa bậc n của một số hữu tỉ x, kí hiệu xⁿ, là tích của n thừa số x (n là số tự nhiên lớn hơn 1)

xn=x⋅x⋅x⋅ ...⋅x⏟n thừa số (x ∈ℚ, n ∈ℕ, n >1)

xⁿ đọc là x mũ n hoặc x lũy thừa n hoặc lũy thừa bậc n của x.

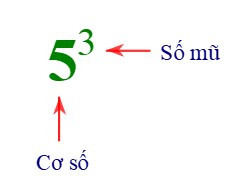
x gọi là cơ số, n gọi là số mũ.

Quy ước: x⁰ = 1 (x ≠ 0); x¹ = x.

Ví dụ:

+ 5³ đọc là 5 mũ 3 hoặc 5 lũy thừa 3 hoặc lũy thừa bậc 3 của 5.

+  Tính (−13)4

(−13)4=−13⋅−13⋅−13⋅−13=(−1)⋅(−1)⋅(−1)⋅(−1)3⋅3⋅3⋅3=181

+ Tính và so sánh: 12262 và (−126)2

12262=14436=4 và (−126)2=(−2)2=4 nên 12262=(−126)2

Chú ý:

• Lũy thừa của một tích bằng tích các lũy thừa; lũy thừa của một thương bằng thương các lũy thừa.

(x⋅y)n=xn⋅yn;                               (xy)n=xnyn (y ≠ 0).

Ví dụ:

(34)15.415=(34.4)15=315;

25³ : 5³ = (255)3=53=125.

6. Nhân và chia hai lũy thừa cùng cơ số

• Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng hai số mũ.

xm⋅xn=xm+n

• Khi chia hai lũy thừa cùng cơ số khác 0, ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ số mũ của lũy thừa chia.

xm:xn=xm−n (x ≠ 0, m ≥ n)

Ví dụ:

+  Tính (23)2.(23)5

 (23)2.(23)5=(23)2+5=(23)7=1282187

+  Tính (−9)5:(−9)4

(−9)5:(−9)4=(−9)5−4=(−9)1=−9.

7. Lũy thừa của lũy thừa

• Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ.

(xm)n=xm⋅n

Ví dụ:

+  Tính [(−3)5]7

 [(−3)5]7=(−3)5⋅7=(−3)35.

Mở rộng

• Lũy thừa với số mũ nguyên âm của một số khác 0.

x−n=1xn với n là số nguyên dương, x ≠ 0.

Ví dụ: 1100=1102=10−2

8. Thứ tự thực hiện các phép tính

• Với các biểu thức chỉ có phép cộng và phép trừ hoặc chỉ có phép nhân và phép chia ta thực hiện các phép tính theo thứ tự từ trái sang phải.

• Với các biểu thức không có dấu ngoặc, ta thực hiện theo thứ tự:

• Với các biểu thức có dấu ngoặc, ta thực hiện trong ngoặc trước, ngoài ngoặc sau.

()→[]→{}

Ví dụ: Tính giá trị của biểu thức:

a) 1,5 – 2³ + 7,5 : 3;

b) 32:(111−522)+74⋅(114−27).

Hướng dẫn giải:

a) 1,5 – 2³ + 7,5 : 3

= 1,5 – 8 + 2,5             (Thực hiện lũy thừa; nhân chia trước)

= – 6,5 + 2,5 = – 4

b) 32:(111−522)+74⋅(114−27)

=32:(−322)+74⋅(−314)                (Thực hiện trong ngoặc trước)

=32⋅(−223)+(−38)                       (Thực hiện nhân chia trước)

=(−11)+(−38)=−918.

9. Quy tắc chuyển vế

• Đẳng thức có dạng A = B. Trong đó A là vế trái; B là vế phải của đẳng thức.

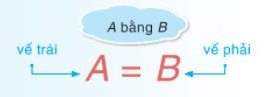
Ví dụ: 4,1 + x = 2,3 là một đẳng thức, trong đó 4,1 + x là vế trái, 2,3 là vế phải.

• Khi biến đổi các đẳng thức, ta thường áp dụng các tính chất sau:

   Nếu a = b thì:          b = a;         a + c = b + c.

• Quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” đổi thành dấu “+”.

+) Nếu a + b = c thì a = c – b;

+) Nếu a – b = c thì a = c + b.

Ví dụ: Tìm x, biết:

a) x+13=−57;

b) x−54=98.

Hướng dẫn giải

a) x+13=−57

x=−57−13       (Quy tắc chuyển vế)

x=−1521−721

x=−2221

Vậy x=−2221.

b) x−54=98

x=98+54                (Quy tắc chuyển vế)

x=98+108

x=198 

Vậy x=198.

B. Bài tập tự luyện

B1. Bài tập tự luận

Bài 1. Viết các biểu thức sau dưới dạng lũy thừa của một số hữu tỉ.

a) 25⁴ . 2⁸;

b) 27² : 25³;

c) 15⁸ . 9⁴;

d) (–27)⁵ : 32³.

Hướng dẫn giải

a) 25⁴ . 2⁸ =(52)4⋅28=52⋅4⋅28=58⋅28=(5⋅2)8=108

b) 27² : 25³ =(33)2:(52)3=36:56=(35)6

c) 15⁸ . 9⁴ =158⋅(32)4=158⋅38=(15⋅3)8=458

d) (–27)⁵ : 32³ = [(−3)3]5:(25)3=(−3)15:215=(−32)15.

Bài 2. Cho trục số sau:

a) Các điểm A, B, C, D biểu diễn những số hữu tỉ nào?

b) Tìm số đối của các số hữu tỉ trên và biểu diễn chúng trên trục số.

Hướng dẫn giải

a) Ta thấy đoạn thẳng đơn vị cũ (ví dụ đoạn từ 0 đến 1) được chia thành 5 phần bằng nhau nên đoạn đơn vị mới bằng 15 đơn vị cũ. Do đó:

Điểm A nằm trước gốc O và cách gốc O một khoảng bằng 7 đơn vị nên nó biểu diễn số hữu tỉ −75.

Tương tự, ta có được:

Điểm B biểu diễn số hữu tỉ −25.

Điểm C biểu diễn số hữu tỉ 45.

Điểm D biểu diễn số hữu tỉ 95.

b) Số đối của −75 là −(−75)=75

Số đối của −25 là −(−25)=25

Số đối của 45 là −45

Số đối của 95 là −95

Biểu diễn trên trục số:

Bài 3. Tính:

a) −818+1527;

b) 3,5−(−27);

c) −0,25⋅(−0,4);

d) −6:315.

Hướng dẫn giải

a) −818+1527=−49+59=19

b) 3,5−(−27)=72+27=4914+414=5314

c) −0,25⋅(−0,4)=0,25 ⋅ 0,4=0,1

d) −6:315=−6:165=−6⋅516=−158

Bài 4. Tính giá trị của các biểu thức sau:

a) (7+314−35)+(0,4−5)−(414−1);

b) 23−[(−74)−(12+38)];

c) (9−12−34):(7−14−58);

d) 3−1−171+17.

Hướng dẫn giải

a) (7+314−35)+(0,4−5)−(414−1)

=7+314−35+0,4−5−414+1

=(7−5+1)+(314−414)+(−35+0,4)

=3+(−1)+(−0,6+0,4)

=2+(−0,2)=1,8

b) 23−[(−74)−(12+38)]

=23−[(−74)−(48+38)]

=23−[(−148)−78]

=23−(−218)

=23+218

=1624+6324=7924

c) (9−12−34):(7−14−58)

=(364−24−34):(568−28−58)

=314:498=314⋅849=6249

d) 3−1−171+17=3−(1−17):(1+17)=3−67:87=3−67⋅78=3−34=124−34=94

Bài 5. Tìm x, biết:

a) x+0,5=−23;

b) x−(−25)=57;

c) 54−6x=712;

d) 3−2x−(54−75)=920.

Hướng dẫn giải

a) x+0,5=−23

x=−23−0,5

x=−23−12

x=−46−36

x=−76

Vậy x=−76.

b) x−(−25)=57

x=57+(−25)

x=57−25

x=2535−1435

x=1135

Vậy x=1135.

c) 54−6x=712

−6x=712−54

−6x=712−1512

−6x=−812

x=−812:(−6)

x=−812⋅−16

x=19

Vậy x=19.

d) 3−2x−(54−75)=920

3−2x−(−320)=920

−2x=920+(−320)−3

−2x=620−3

−2x=310−3010

−2x=−2710

x=−2710:(−2)

x=2720

Vậy x=2720.

Bài 6. Tính một cách hợp lí.

a) 4,64+(−12)3+0,62−3⋅−38;

b) 2022,123⋅2023+2022,123⋅(−2023)2022−2021.

Hướng dẫn giải

a) 4,64+(−12)3+0,62−3⋅−38

=4,64+−18+0,36−−98

=(4,64+0,36)+(−18−−98)

=5+(−18+98)

=5+88=5+1=6

b) 2022,123⋅2023+2022,123⋅(−2023)2022−2021

=2022,123⋅2023+2022,123⋅(−2023)

=2022,123⋅[2023+(−2023)]

=2022,123⋅0=0

Bài 7. Tính:

a) (−212)3;

b) (−212)4;

c) (1+12−14)2⋅20220;

d) 2:(12−23)3.

Hướng dẫn giải

a) (−212)3=(−52)3=−1258

b) (−212)4=(−52)4=62516

c) (1+12−14)2⋅20220=(54)2⋅1=2516

d) 2:(12−23)3=2:(36−46)3=2:(−16)3=2:−1216=2⋅(−216)=−432

Bài 8. Tính một cách hợp lí.

a) 334+(−0,7)+54+(−4,3);

b) 235⋅(−2022)+0,45⋅94−2,6⋅(−2022)+0,55⋅94;

c) (6−53+12)−(3+23−32)−(5+52−73);

d) −2,4⋅174+127⋅−856−2,4⋅(−554)−127⋅−716.

Hướng dẫn giải

a) 334+(−0,7)+54+(−4,3)

=3,75+(−0,7)+1,25+(−4,3)

=(3,75+1,25)+[(−0,7)+(−4,3)]

=5+(−5)=0

b) 235⋅(−2022)+0,45⋅94−2,6⋅(−2022)+0,55⋅94

=2,6⋅(−2022)−2,6⋅(−2022)+(0,45+0,55)⋅94

 

=(2,6−2,6)⋅(−2022)+1⋅94

=0⋅(−2022)+94

=0+94=94

c) (6−53+12)−(3+23−32)−(5+52−73)

=6−53+12−3−23+32−5−52+73

=(6−3−5)−(53+23−73)+(12+32−52)

=−2−0+(−12)

=−42+(−12)=−52

d) −2,4⋅174+127⋅−856−2,4⋅(−554)−127⋅−716

=−2,4⋅[174+(−554)]+127⋅(−856−−716)

=−2,4⋅(174+−254)+127⋅(−856+716)

=−2,4⋅(−84)+127⋅(−146)

=−2,4⋅(−2)+127⋅(−73)

=4,8+(−4)=0,8

Bài 9. Tìm x, biết:

a) x:(−12)3=−12;

b) (34)5⋅x=(34)7;

c) 343125=(75)x;

d) (−13)x=−1243.

Hướng dẫn giải

a) x:(−12)3=−12

x=−12⋅(−12)3

x=(−12)3+1

x=(−12)4=116.

 Vậy x=116.

b) (34)5⋅x=(34)7

x=(34)7:(34)5

x=(34)7−5

x=(34)2=916.

Vậy x=916.

c) 343125=(75)x

(75)3=(75)x

x=3.

Vậy x = 3.

d) (−13)x=−1243

(−13)x=(−13)5

x=5.

Vậy x = 5.

Bài 10. Tính:

a) 42⋅43210;

b) 54⋅204255⋅45;

c) 27⋅9365⋅82;

d) 63+3⋅62+33−13.

Hướng dẫn giải

a) 42⋅43210=45210=(22)5210=210210=1

b) 54⋅204255⋅45=(5⋅20)4(25⋅4)5=10041005=1100

c) 27⋅9365⋅82=27⋅(32)3(2⋅3)5⋅(23)2=27⋅3625⋅35⋅26=27⋅36211⋅35=324=316

d) 63+3⋅62+33−13=33⋅23+3⋅32⋅22+33−13=33⋅(23+22+1)−13=27⋅13−13=−27

Bài 11. So sánh:

a) – 1,25 và – 1,125;

b) 0,8 và −1019;

c) −219 và −1019;

d) 223 và 176;

e) 12022 và 12023;

f) – 5,6 và 12;

g) 79 và 1,5.

Hướng dẫn giải

a) Có 1,25 > 1,125 nên – 1,25 < – 1,125

b) Có 0,8 = 810=45=1215, vì 1215 > 815. Nên 0,8 > 815

c) Có 219 < 1019 nên −219 > −1019

d) Có 223=83=166, vì 166 < 176. Nên 223 < 176

e) 12022 > 12023

f) Có – 5,6 < 0 và 12 > 0. Nên – 5,6 < 12

g) Có  79 < 1 và 1,5 >1. Nên 79 < 1,5

Bài 12. Tính giá trị của biểu thức sau:

a) (23+16):54+(14+38):52;

b) 2:(12−23)2+0,253⋅43−(−12)4:64;

c) 7⋅23−5⋅{[10,51+4⋅(34−25)2]−20220}.

Hướng dẫn giải

a) (23+16):54+(14+38):52

=(46+16)⋅45+(28+38)⋅25

=56⋅45+58⋅25

=23+14

=812+312

=1112

b) 2:(12−23)2+0,253⋅43−(−12)4:64

=2:(−16)2+(14)3⋅43−(−2⋅6)4:64

=2⋅136+1343⋅43−(−2)4⋅(6)4:64

=2⋅36+1−(−2)4

=72+1−16=57

c) 7⋅23−5⋅{[10,51+4⋅(34−25)2]−20220}

=7⋅8−5⋅{[10,51+4⋅(720)2]−1}

=56−5⋅{[10,51+4⋅49400]−1}

=56−5⋅{[10,51+49100]−1}

=56−5⋅{[10,51+0,49]−1}

=56−5⋅{11−1}

=56−5⋅10=6

B2. Bài tập trắc nghiệm

Bài 1. Điểm biểu diễn số đối của của số hữu tỉ −12 là

A. điểm A;

B. điểm B;

C. điểm C;

D. điểm D.

Hướng dẫn giải

Đáp án đúng là: C

Điểm biểu diễn số hữu tỉ đối của −12 nằm khác phía với −12 so với điểm O. Như vậy điểm này nằm sau O.

Khoảng cách tử O đến −12 là 3 đoạn nên khoảng cách từ O đến điểm đó cũng là 3 đoạn.

Vậy điểm biểu diễn số hữu tỉ đối của −12 là điểm C.

Bài 2. Tính 7⋅23−5{[10,51+4⋅(34−25)2]−20210}

A. 6;

B. 2021;

C. 56;

D. 51.

Hướng dẫn giải

Đáp án đúng là: A

7⋅23−5{[10,51+4⋅(34−25)2]−20210}

=7⋅8−5{[10,51+4⋅(720)2]−1}

=56−5{[10,51+4⋅49400]−1}

=56−5{[10,51+49100]−1}

=56−5{[10,51+0,49]−1}

=56−5{11−1}

=56−5⋅10=6

Bài 3. Trong các số hữu tỉ: −112; −5; 0,75; 45. Số đối của số hữu tỉ lớn nhất là

A. 45;

B. 5;

C. – 0,75;

D. −45.

Hướng dẫn giải

Đáp án đúng là: D

Ta có: −112 = −32; −5 = −102 mà −102 < −32 < 0 nên −5 < −112 < 0

0,75 = 34 = 1520; 45 = 1620 mà 1620 > 1520 > 0 nên 45 > 0,75 > 0

Do đó: −5 < −112 < 0,75 < 45

Suy ra số lớn nhất là 45

Vậy số đối của 45 là −45.

Bài 4. Tập hợp số hữu tỉ được kí hiệu là

A. ℕ;

B. ℤ;

C. ℚ;

D. ℝ.

Hướng dẫn giải

Đáp án đúng là: C

Tập hợp số hữu tỉ được kí hiệu là ℚ.

Bài 5. Giá trị của biểu thức 35−(12−25) là

A. −310;

B. 12;

C. 32;

D. 710.

Hướng dẫn giải

Đáp án đúng là: B

35−(12−25) = 35−12+25 = (35+25)−12 = 1−12 = 12.

Bài 6. Giá trị của biểu thức 6,25+[1,75−(0,75−2,75)] là

A. 6;

B. 6,5;

C. 9,5;

D. 10.

Hướng dẫn giải

Đáp án đúng là: D

6,25+[1,75−(0,75−2,75)] 

= 6,25+[1,75−0,75+2,75] 

= 6,25+1,75−0,75+2,75

= (6,25+2,75)+(1,75−0,75)

= 9 + 1

= 10

Câu 7. Tính 252⋅253510

A. 5;

B. 25;

C. 1;

D. 15.

Hướng dẫn giải

Đáp án đúng là: C

252⋅253510=255510=(52)5510=510510=1

Câu 8. Tìm x, biết x:(−12)5=(−12)3

A. x=1256;

B. x=116;

C. x=−1256;

D. x=−116.

Hướng dẫn giải

Đáp án đúng là: A

x:(−12)5=(−12)3

x=(−12)3⋅(−12)5

x=(−12)5+3

x=(−12)8=1256. Vậy x=1256

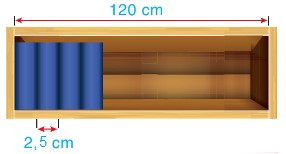
Bài 9. Ngăn đựng sách của một giá sách trong thư viện dài 120 cm (xem hình dưới). Người ta dự định xếp các cuốn sách dày khoảng 2,5 cm vào ngăn này. Hỏi ngăn sách đó có thể để được nhiều nhất bao nhiêu cuốn sách như vậy?

A. 50 cuốn sách;

B. 48 cuốn sách;

C. 40 cuốn sách;

D. 25 cuốn sách.

Hướng dẫn giải

Đáp án đúng là: B

Ngăn sách đó có thể để được nhiều nhất số cuốn sách như thế là:

120 : 2,5 = 48 (cuốn sách).

Bài 10. Tìm x, biết: 3−3x−(54−75)=920

A. x=910;

B. x=−910;

C. x=109;

D. x=−109.

Hướng dẫn giải

Đáp án đúng là: A

3−3x−(54−75)=920

3−3x−(−320)=920

−3x=920+(−320)−3

−3x=620−3

−3x=310−3010

−3x=−2710

x=−2710:(−3)

x=910. Vậy x=910

Bài 11. Một ô tô đã đi 110 km trong 3 giờ. Trong giờ thứ nhất, xe đi được 13 quãng đường. Trong giờ thứ hai, xe đi được 25 quãng đường còn lại. Hỏi trong giờ thứ ba xe đi được bao nhiêu ki-lô-mét?

A. 45 km;

B. 44 km;

C. 47 km;

D. 46 km.

Hướng dẫn giải

Đáp án đúng là: B

Giờ thứ nhất đi được số ki-lô-mét là: 110⋅13 = 1103 (km)

Giờ thứ hai đi được số ki-lô-mét là: (110−1103)⋅25 = 883 (km)

Giờ thứ ba xe đi được số ki-lô-mét là: 110−(1103+883) = 44 (km)

Câu 12. Khoảng cách từ Trái Đất đến Mặt Trời bằng khoảng 1,5 . 10⁸ km. Khoảng cách từ Mộc tinh đến Mặt Trời khoảng 7,78 . 10⁸ km. Hỏi khoảng cách từ Mộc tinh đến Mặt Trời gấp khoảng bao nhiêu lần khoảng cách từ Trái Đất đến Mặt Trời?

A. 5 lần;

B. 5 . 10⁸ lần;

C. 8 lần;

D. 10⁸ lần.

Hướng dẫn giải

Đáp án đúng là: A

Khoảng cách từ Mộc tinh đến Mặt Trời gấp khoảng cách từ Trái Đất đến Mặt Trời số lần là: (7,78 . 10⁸) : (1,5 . 10⁸) = 7,78 : 1,5 ≈ 5 (lần).