Toptailieu.vn biên soạn và giới thiệu Lý thuyết Số vô tỉ. Căn bậc hai số học (Cánh Diều) Toán 7 hay, ngắn gọn và bài tập tự luyện có lời giải chi tiết sẽ giúp học sinh nắm vững nội dung kiến thức từ đó dễ dàng làm các bài tập Toán 7.
Lý thuyết Số vô tỉ. Căn bậc hai số học (Cánh Diều) Toán 7
A. Lý thuyết
1. Số vô tỉ
1.1 Khái niệm số vô tỉ
Trong đời sống thực tiễn của con người, ta thường gặp những số không phải là số hữu tỉ. Những số không phải là số hữu tỉ được gọi là số vô tỉ.
Ví dụ: Số Pi (π) là tỉ số giữa độ dài của một đường tròn với độ dài đường kính của đường tròn đó và là một số vô tỉ.
1.2 Số thập phân vô hạn không tuần hoàn
Những số thập phân vô hạn mà phần thập phân của nó không có một chu kì nào cả, những số đó được gọi là số thập phân vô hạn không tuần hoàn.
Ví dụ:
Số –1,359130000110578… là số thập phân vô hạn không tuần hoàn.
Số π = 3,14159265358979323846264338… là số thập phân vô hạn không tuần hoàn.
1.3 Biểu diễn thập phân của số vô tỉ
Số vô tỉ được viết dưới dạng số thập phân vô hạn không tuần hoàn.
Ví dụ:
Số –1,359130000110578… là số vô tỉ.
Số π = 3,14159265358979323846264338… là số vô tỉ.
- Nếu a là một số tự nhiên, số nguyên hay số hữu tỉ thì a không thể là số vô tỉ.
2. Căn bậc hai số học
- Căn bậc hai số học của một số a không âm là số x không âm sao cho x2 = a.
- Căn bậc hai số học của số a (a ≥ 0) được kí hiệu là .
- Căn bậc hai số học của số 0 là số 0, viết là: .
Chú ý: Cho a ≥ 0. Khi đó:
+ Đẳng thức = b là đúng nếu b ≥ 0 và b2 = a.
+ .
Ví dụ:
- Ta có 9 > 0 và 92 = 81 nên 9 là căn bậc hai số học của 81. Ta viết: .
- Ta có 0,4 ≥ 0 và (0,4)2 = 0,16 nên 0,4 là căn bậc hai số học của 0,16.
Ta viết .
- Ta có (– 5)2 = 25 nhưng – 5 < 0 nên – 5 không phải căn bậc hai số học của số 25.
Nhận xét:
- Nếu số nguyên dương a không phải là bình phương của bất kì số nguyên dương nào thì là số vô tỉ.
Ví dụ: đều là các số vô tỉ.
- Ta có thể tính được giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số dương bằng máy tính cầm tay.
Ví dụ: Để tính và bằng máy tính cầm tay ta làm như sau:
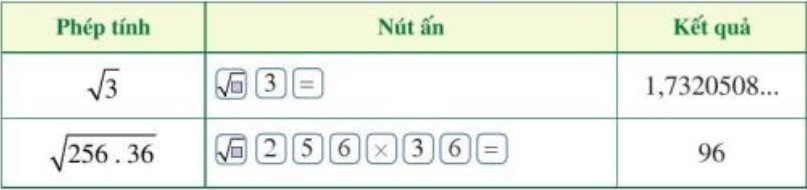
B. Bài tập tự luyện
B.1 Bài tập tự luận
Bài 1. Chứng tỏ rằng:
a) 12 là căn bậc hai số học của 144.
b) – 0,2 không phải là căn số học của 0,04.
Hướng dẫn giải
a) Ta có 12 ≥ 0 và 122 = 144 nên 12 là căn bậc hai số học của 144, ta viết .
b) Ta có (– 0,2)2 = 0,04 nhưng – 0,2 < 0 nên – 0,2 không phải là căn bậc hai số học của 0,04.
Bài 2. Tìm giá trị của:
a) ;
b) .
Hướng dẫn giải
a) (vì ).
b) (vì (0,7)2 = 0,49).
Bài 3. Tính giá trị của biểu thức
a) ;
b) .
Hướng dẫn giải
a) Ta có và .
Nên .
b) Ta có và .
Nên .
B.2 Bài tập trắc nghiệm
Câu 1. Tính .
A. –8;
B. 8;
C. ±8;
D. 32.
Hướng dẫn giải
Đáp án đúng là: B.
Sử dụng định nghĩa về căn bậc hai số học.
Căn bậc hai số học của số a không âm là số x không âm sao cho x2 = a.
Vì 82 = 64 và 8 > 0 nên .
Câu 2. Cho và . Phát biểu nào sau đây là đúng?
A. a < b;
B. a = b;
C. a ≠ b;
D. a > b.
Hướng dẫn giải
Đáp án đúng là: B.
Ta có ;
Do đó hay a = b.
Vậy a = b.
Câu 3. Sau khi sơn tường cho một bức tường hình vuông bác Phương phải trả cho thợ sơn là 1 280 000 đồng. Biết công thợ sơn cho 1 m2 là 20 000 đồng. Độ dài cạnh bức tường đó là:
A. 8 m;
B. 32 m;
C. 64 m;
D. 64 m2.
Hướng dẫn giải
Đáp án đúng là: A.
Diện tích bức tường cần sơn là: 1 280 000 : 20 000 = 64 (m2)
Diện tích của hình vuông có cạnh a (m) là a2 (m2).
Bức tường hình vuông có diện tích là 64 m2 nên ta có a2 = 64
Vì cạnh hình vuông nên a không thể âm, do đó a là căn bậc hai số học của 64.
Ta có 82 = 64 và 8 > 0 nên .
Suy ra a = 8 (m).
Vậy độ dài cạnh bức tường hình vuông đó là 8 m.
Xem thêm Lý thuyết các bài Toán 7 Cánh Diều hay, chi tiết khác:
Lý thuyết Bài 2. Tập hợp R các số thực
Lý thuyết Bài 3. Giá trị tuyệt đối của một số thực
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.