Toptailieu.vn xin giới thiệu 50 bài tập trắc nghiệm Ôn tập chương 2 (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 12 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

Ôn tập chương 2

Câu 1: Hình trụ (H) có diện tích xung quanh là 6π(cm²) và thể tích khối trụ là 9π(cm³). Chiều cao của hình lăng trụ là :

A. 1(cm)

B. 3(cm)

C. 1/2 (cm)

D. 2(cm)

Lời giải:

Từ giả thiết ta có:

Đáp án cần chọn là:A

Câu 2: Cho hình nón tròn xoay có đường cao 12cm và đường kính đáy 10cm. Độ dài đường sinh của hình nón là :

A. √119 (cm)

B. 17(cm) 

C. 15(cm)

D. 13(cm)

Lời giải:

Từ giả thiết ta có:

Đáp án cần chọn là:D

Câu 3:Cho hình nón tròn xoay có đỉnh là S, O là tâm của đường tròn đáy, đường sinh bằng a√2 và góc giữa đường sinh và mặt phẳng đáy bằng 60° . Diện tích xung quanh S_xq của hình nón và thể tích V của khối nón tương ứng là:

Lời giải:

Gọi A là một điểm thuộc đường tròn đáy hình nón. Theo giải thiết ta có đường sinh SA = a√2 và góc giữa đường sinh và mặt phẳng đáy là 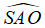 = 60° .

Đáp án cần chọn là:A

Câu 4: Một hình trụ có bán kính đáy bằng a và có thiết diện qua trục là một hình chữ nhật có diện tích là 2a² . Diện tích xung quanh của hình trụ là :

A. 4πa²

B. 3πa²

C. 2πa²

D. πa²

Lời giải:

Từ giả thiết ta có: r = a; 2a.h = 2a² => h = a => S_xq = 2πrh = 2πa²

Đáp án cần chọn là:C

Câu 5: Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng 6π (cm) và thiết diện đi qua trục là một hình chữ nhật có độ dài đường chéo bằng 10 (cm) .

A. 48π (cm³)

B. 24π (cm³)

C. 72π (cm³)

D. 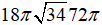 (cm³)

Lời giải:

Gọi O, O' là hai tâm của đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD .

Do chu vi đáy của hình trụ đó bằng 6π (cm) nên bán kính đáy của hình trụ là

Đáp án cần chọn là:C

Câu 6: Cho khối trụ có diện tích toàn phần là 6πa² và thể tích là 2πa³. Bán kính đáy của hình trụ là :

A. 3a/2

B. a

C. 2a/3

D. 2a

Lời giải:

Từ giả thiết ta có:

Đáp án cần chọn là:B

Câu 7:Cho hình nón đỉnh S với đáy là đường tròn tâm O bán kính R . Gọi I là một điểm nằm trên mặt phẳng đáy sao cho OI = R√3 . Giả sử A là điểm nằm trên đường tròn (O; R) sao cho OA ⊥ OI . Biết rằng tam giác SAI vuông cân tại S . Khi đó, diện tích xung quanh S_xq của hình nón và thể tích V của khối nón là:

Lời giải:

Đáp án cần chọn là:A

Câu 8: Cho hình chóp S.ABC có đáy ABC là tam giác vuông đỉnh A và BC = a. Cạnh bên SB vuông góc với mặt phẳng (ABC), SC tại với mặt phẳng (ABC) một góc là 60^o. Bán kính mặt cầu ngoại tiếp hình chóp là :

A. a√3

B. a√2

C. a√3/2

D. a

Lời giải:

Ta có:

Gọi I là trung điểm của SC. Theo định lí ba đường vuông góc ta có tam giác SAC vuông tại A, mà tam giác SBC vuông tại B nên I cách đều các đỉnh của hình chóp hay I là tâm mặt cầu ngoại tiếp hình chóp. Khi đó ta có bán kính: r = SC/2 = a

Đáp án cần chọn là:D

Câu 9: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AD = a; AB' = 2a. Diện tích mặt cầu ngoại tiếp tứ diện ACB’D’ là :

A. 5πa²

B. 3πa²

C. 5πa²/4

D. 5πa²/3

Lời giải:

Ta có mặt cầu ngoại tiếp tứ diện ACB’D’ cũng chính là mặt cầu ngoại tiếp hình hộp chữ nhật nên có bán kính

Đáp án cần chọn là:A

Câu 10:Một cái tháp khổng lồ có thân là hình trụ và mái là một nửa hình cầu. Người ta muốn sơn toàn bộ mặt ngoài của thắp (kể cả mái). Tính diện tích S cần sơn (làm tròn đến mét vuông).

A. S = 8243 (m²)

B. S = 11762 (m²)

C. S = 12667 (m²)

D. S = 23524 (m²)

Lời giải:

Đáp án cần chọn là:A

Câu 11: Cho hình vuông ABCD cạnh 8 cm. Gọi M, N lần lượt là trung điểm của AB và CD. Quay hình vuông ABCD xung quanh MN. Diện tích xung quanh của hình trụ tạo thành là:

A.64π (cm² )

B. 32π (cm² )

C.96π (cm² )

D. 126π (cm² )

Lời giải:

Khi quay hình vuông ABCD xung quanh MN ta được hình trụ có chiều cao BC = 8 cm; bán kính đáy MA = 4 cm

S_xq=2πrh=2π.4.8=64π (cm² )

Đáp án cần chọn là:A

Câu 12: Một hình trụ (T) có diện tích toàn phần là 120π (cm² ) và có bán kính đáy bằng 6 cm. Chiều cao của (T) là:

A. 6 cm

B. 5 cm

C. 4 cm

D. 3 cm

Lời giải:

S_tp=2πrh+2πr²⇒120π=2π.6.h+2π.6²⇒h=4(cm)

Đáp án cần chọn là:C

Câu 13: Một hình trụ có tỉ số giữa diện tích toàn phần và diện tích xung quanh bằng 4. Khẳng định nào sau đây là đúng:

A. Đường sinh bằng bán kính đáy

B. Bán kính đáy bằng ba lần đường sinh

C. Đường sinh bằng ba lần bán kính đáy

D. Đường sinh bằng bốn lần bán kính đáy

Lời giải:

Ta có:

Vậy bán kính bằng ba lần đường sinh

Đáp án cần chọn là:B

Câu 14: Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2. Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần S_tp của hình trụ đó.

A.4π

B.2π

C.6π

D.10π

Lời giải:

Quay hình chữ nhật ABCD xung quanh trục MN, ta được một hình trụ có chiều cao AB =1; bán kính đáy AM = 1

S_tp=2πrh+2πr²=2π.1.1+2π.1²=4π

Đáp án cần chọn là:A

Câu 15: Cho một hình trụ (H) có trục ∆. Một mặt phẳng (P) song song với trục ∆ và cách trục ∆ một khoảng k. Nếu k > r thì kết luận nào sau đây là đúng:

A. Mp (P) tiếp xúc với mặt trụ theo một đường sinh.

B. Mp (P) cắt mặt trụ theo hai đường sinh.

C. Mp (P) cắt mặt trụ theo một đường sinh.

D. Mp (P) không cắt mặt trụ.

Lời giải:

Đáp án : A

Đáp án cần chọn là:A

Câu 16: Khối trụ có thiết diện qua trục là một hình vuông cạnh bằng a. Mệnh đề nào dưới đây là mệnh đề sai:

Lời giải:

Thiết diện là hình vuông BCC’B’ cạnh a

⇒ BB'=a; OB= a/2

Diện tích xung quanh của hình trụ là:

Diện tích toàn phần của hình trụ là:

Thể tích của hình trụ là:

Đáp án cần chọn là:C

Câu 17. Cho hình chữ nhật ABCD có AB = a và góc 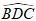 = 30⁰ . Quay hình chữ nhật này xung quanh cạnh AD. Diện tích xung quanh của hình trụ được tạo thành là:

A. √3πa²    

B. 2√3πa²  

C. 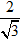 πa²

D. πa²

Lời giải:

+ Khi quay hình chữ nhật này xung quanh cạnh AD ta được hình trụ như hình vẽ.

Hình trụ tạo thành có:

+ Bán kính đường tròn đáy là r = AB = a

+ Đường cao của hình trụ là:
h = BC = CD.tan30⁰ = 

Suy ra, diện tích xung quanh của hình trụ tạo thành là:

Đáp án cần chọn là:C

Câu 18. Cho hình trụ tròn xoay có hai đáy là hai hình tròn (O; R) và ( O’: R’). Tồn tại dây cung AB thuộc đường tròn (O) sao cho tam giác O’AB là tam giác đều và mặt phẳng (O’AB) hợp với mặt phẳng chứa đường tròn (O) một góc 60⁰. Khi đó, diện tích xung quanh Sxq hình trụ và thể tích V của khối trụ tương ứng là:

Lời giải:

+ Ta có OO’ là trục của hình trụ nên
OO' ⊥ (OAB) .

Gọi H là trung điểm của AB thì

Giả sử OH = x.
Khi đó: 0 < x < R và OO' = x.tan60⁰ = x√3 .

+ Xét tam giác OAH, ta có: AH² = R² – x².

+ Vì tam giác O’AB đều nên:
O'A = AB = 2AH = 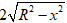 (1)

Mặt khác, tam giác AOO’ vuông tại O nên:

AO’² = OO’² + R² = 3x² + R². (2)

Từ (1),(2) ⇒ 4(R² - x²) = 3x² + R² ⇒ x² = 

⇒ h = OO' = x√3 = 

Gọi S là diện tích xung quanh và V là thể tích của hình trụ thì ta có:

Đáp án cần chọn là:B

Câu 19. Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc 45⁰. Diện tích xung quanh hình trụ và thể tích V của khối trụ là:

Lời giải:

* Gọi M, N theo thứ tự là trung điểm của AB và CD.

Khi đó: OM ⊥ AB và O'N ⊥ DC

Gọi I là giao điểm của MN và OO’.
Đặt R = OA, h = OO’.

* Trong tam giác IOM vuông cân tại I nên:

* Ta có:
R² = OA² + AM² + MO² .

Đáp án cần chọn là:D

Câu 20. Cho hình chữ nhật ABCD cạnh AB = 6; AD = 4 quay quanh AB ta được hình trụ có diện tích xung quanh bằng:

A. S_xq = 8π .

B. S_xq = 48π .

C. S_xq = 50π

D. S_xq = 32π .

Lời giải:

Khi quay hình chữ nhật quanh cạnh AB ta được hình trụ có chiều cao h = AB = 6, bán kính đường tròn đáy là R = AD = 4.

Do đó, diện tích xung quanh của hình trụ là:

S = 2πR.h = 2π.4.6 = 48π

Đáp án cần chọn là:B

Câu 21. Trong không gian, cho hình chữ nhật ABCD có AB = 1 và AD = 2. Gọi M,N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần Stp của hình trụ đó

A. S_tp = 4π.

B. S_tp = 2π .

C. S_tp = 6π .

D. S_tp = 10π .

Lời giải:

Khi quay hình chữ nhật quanh trục MN ta được hình trụ có:

+ chiều cao: h = AB = 1 .

+ bán kính đường tròn đáy là r = 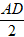 = 1

Do đó,diện tích toàn phần của hình trụ đó là:

S_tp = 2πrh + 2πr² = 2π.1.1 + 2π.1² = 4π

Đáp án cần chọn là:A

Câu 22. Một hình thang vuông ABCD có đường cao AD = π, đáy nhỏ AB = π , đáy lớn CD = 2π . Cho hình thang quay quanh CD, ta được khối tròn xoay có thể tích bằng

A. V = 2π⁴

B. V = 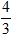 π⁴ .

C. V = 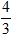 π³

D. V = 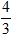 π² .

Lời giải:

Khi quay hình thang quanh CD ta được khối tròn xoay gồm 2 phần:

+ Khối V₁ là khối trụ có bán kính đáy AD = π và chiều cao AB = π nên thể tích khối trụ tạo thành là:
V₁ = π.π².π = π⁴

+ Khối V₂ là khối nón có bán kính đường tròn đáy là BE = π và đường cao BC = π nên thể tích của khối nón là:
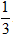
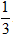
V₂ =  .π.π².π =  .π⁴

Vậy thể tích khối tròn xoay cần tính là :
V = V₁ + V₂ = 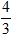 π⁴

Đáp án cần chọn là:B

Câu 23. Cho hình chữ nhật ABCD có AB = nAD. Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD ta được khối trụ có diên tích toàn phần là S₁, khi quay hình chữ nhật ABCD một vòng quanh cạnh AD ta được khối trụ có diên tích toàn phần là S₂. Khẳng định nào sau đây là đúng?

A. nS₁ = S₂

B. S₁ = nS₂.

C. S₁ = ( n+ 1).S₂

D. S₂ = (n+1)S₁

Lời giải:

* Khi quay hình chữ nhật ABCD một vòng quanh cạnh CD ta được khối trụ có bán kính
r₁ = AD; h₁ = AB

* Khi đó
S₁ = 2π.AD.AB + 2π.AD²
= 2π(nAD² + AD²)

* Tương tự khi quay hình chữ nhật ABCD một vòng quanh cạnh AD ta có:
r₂ = AB; h₂ = AD

* Khi đó S₂ = 2π(nAD² + n²AD)

Do đó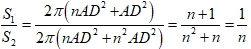
 .

Suy ra: nS₁ = S₂

Đáp án cần chọn là:A

Câu 24. Cho hình chữ nhật ABCD với AB = 1,
BC = 3. Đường thẳng d nằm trong mặt phẳng (ABCD), song song AD và cách AD một khoảng 2 ; đồ thị không có điểm chung với hình chữ nhật ABCD. Tính thể tích khối tròn xoay tạo được khi quay hình chữ nhật ABCD quanh d.

A. 15π .

B. 27π .

C. 12π .

D. 10π

Lời giải:

* BC cách đường d một khoảng d’ = 2+ AB = 3

*Do đó khối tròn xoay là tập hợp các điểm nằm ở giữa hai hình trụ có bán kính lần lượt là 2 và 3, chiều cao của hai hình trụ đều là 3.

Thể tích khối tròn xoay bằng hiệu thể tích của hai khối trụ nêu trên là:

V = 3².3.π - 2².3.π = 15π

Đáp án cần chọn là:A

Câu 25. Cho một hình lăng trụ tam giác đều ABC.A’B’C’ có AB= a. Biết mặt phẳng (AB’C’) hợp với mặt đáy (A’B’C’) một góc bằng 45⁰. Cho một hình trụ ngoại tiếp hình lăng trụ ABC.A’B’C’ (hình trụ có các đường tròn đáy ngoại tiếp các mặt của hình lăng trụ). Tính diện tích xung quanh của hình trụ và thể tích khối trụ.

Lời giải:

Gọi I là trung điểm B’C’.

Vì ABC.A’B’C’ là lăng trụ đều nên AI ⊥ B'C'
và A'I ⊥ B'C' .

Do đó góc giữa ( AB’C’) và (A’B’C’) là 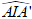 = 45⁰ .

Suy ra tam giác AA’I vuông cân tại A’ nên
AA’ = A’I = 

Suy ra: 

Do đó diện tích xung quanh:

Thể tích khối trụ là:

Đáp án cần chọn là:A

Câu 26. Cho một hình nón đỉnh S, mặt đáy là hình tròn tâm O, bán kính R = 6cm và có thiết diện qua trục là tam giác đều. Cho một hình trụ có hai đường tròn đáy là (O; r) và (I; r), có thiết diện qua trục là hình vuông, biết đường tròn (O; r) nằm trên mặt đáy của hình nón, đường tròn (I; r) nằm trên mặt xung quanh của hình nón ( I thuộc đoạn SO). Tính thể tích khối trụ.

A. 432π(26√3 - 45) .

B. 1296π(26√3 - 45) .

C. 1296π(7 - 4√3) .

D. 432π(7 - 4√3) .

Lời giải:

* Hình nón có bán kính đường tròn đáy
R = 6cm và có thiết diện qua trục là tam giác đều nên có

SM = 2R = 12cm, SO = SM.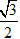 = 6√3

* Đặt SI = x, vì BI // AO nên ta có:

Chiều cao của hình trụ là:
h = OI = SO - SI = 6√3 - x

Do đó, thiết diện qua trục của hình trụ là hình vuông khi và chỉ khi:

Khi đó: h = 6√3 - x = 12(2√3 - 3);
r = 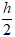 = 6(2√3 - 3)

Thể tích khối trụ là:

V = πr²h
= π.[6(2√3 - 3)]².12(2√3 - 3)
= 1296π(26√3 - 45)

Đáp án cần chọn là:B

Câu 27. Cho hình trụ nội tiếp mặt cầu tâm O, biết thiết diện qua trục là hình vuông và diện tích mặt cầu bằng 72π . Tính diện tích xung quanh của hình trụ.

A. 12π

B. 16π

C. 18π

D. 36π

Lời giải:

Ta có diện tích của mặt cầu là:
S_mc = 4πR² = 72π ⇔ R = 3√2

Thiết diện qua trục của hình trụ là hình vuông nên h = 2r.

Nên: R = r√2 = 3√2 ⇔ r = 3 ⇒ h= 6.

Do đó diện tích xung quanh hình trụ là:
S = 2πrh = 2π.3.6 = 36π

Đáp án cần chọn là:D

Câu 28: Hình nón có chiều dài đường sinh d, bán kính đáy r thì có diện tích xung quanh bằng:

A.πrd

B.2πrd

C.πrl

D.2πrl

Lời giải:

Đáp án : A

Đáp án cần chọn là:A

Câu 29: Hình nón có đường sinh l=5cm và bán kính đáy r=4cm thì có diện tích xung quanh bằng:

A.20π (cm² )

B.40π (cm² )

C.20 (cm² )

D.20π (cm³ )

Lời giải:

S_xq=πrl=π.5.4=20π (cm² )

Đáp án cần chọn là:A

Câu 30: Hình nón bán kính đáy r=3cm và chiều cao h=4cm thì có diện tích toàn phần bằng:

A.24π (cm² )

B.39π (cm² )

C.20π(cm² )

D.20π (cm³ )

Lời giải:

Độ dài đường sinh:

S_tp=πr²+πrl=π3²+π.3.5=24π (cm² )

Đáp án cần chọn là:A

Câu 31: Một hình nón có đường sinh bằng đường kính đáy và bằng 2R. Diện tích xung quanh của hình nón bằng:

A.(πR²)/2 

B.πR²

C.2πR²

D.4πR²

Lời giải:

Độ dài đường sinh: l = 2R

Bán kính đáy: r = R

S_xq=πrl=π.R.2R=2πR²

Đáp án cần chọn là:C

Câu 32: Cho tam giác ABC vuông tại A, biết AB=a√3 và ∠(ACB)=60º. Khi quay hình tam giác ABC quanh cạnh AC thì khối nón tròn xoay được tạo thành có thể tích bằng:

A.πa³  

B.3πa³

C.9πa³

D.6πa³

Lời giải:

Xét tam giác ABC vuông tại A có:

Khi quay hình tam giác ABC quanh cạnh AC ta được hình nón có chiều cao AC, bán kính đáy AB

Đáp án cần chọn là:A

Câu 33: Cho tam giác ABC vuông tại A. Khi quay tam giác ABC quanh cạnh BC thì đường gấp khúc BAC tạo thành

A. Hình nón

B. Hai hình nón

C. Mặt nón

D. Khối nón

Lời giải:

Kẻ AH vuông góc với BC taị H

Khi quay đường gấp khúc BAC quanh cạnh BC ta thu được hai hình nón:

(N₁): r₁=AH; h₁=BH; l₁=AB

(N₂): r₂=AH; h₂=CH; l₂=AC

Đáp án cần chọn là:B

Câu 34: Quay một tam giác vuông cân có cạnh huyền bằng a√2 xung quanh một cạnh góc vuông. Tính diện tích xung quanh của hình nón được tạo thành:

A.2πa² √2

B.πa² √2 

C.2πa²

D.πa²

Lời giải:

Quay tam giác vuông cân ABC quanh cạnh góc vuông AC ta được hình nón có chiều cao AC, bán kính đáy AB và đường sinh BC

Ta có AB=BC/√2=a

S_xq=πRl=π.AB.BC=π.a.a√2= πa² √2

Đáp án cần chọn là:B

Câu 35: Cho hình chóp tứ giác đều S.ABCD có chiều cao h = 2 và ∠(ASB)=60º. Khi đó diện tích xung quanh của hình nón ngoại tiếp hình chóp bằng:

A.π

B.2π

C.2√2 π

D.4√2 π

Lời giải:

Gọi O là tâm hình vuông ABCD ⇒ SO ⊥ (ABCD)

S.ABCD là hình chóp tứ giác đều ABCD là hình vuông và các cạnh bên bằng nhau.

∆SAB có SA = SB; ∠(ASB)=60º nên ∆SAB đều

Đặt SA = AB = a.

ABCD là hình vuông cạnh a nên

Ta có:

AO²+SO²=SA² ⇒ a²/2+4=a² ⇒ a=2√2

Hình nón ngoại tiếp hình chóp có bán kính đáy r=OA=2; đường sinh

l=SA=2√2

⇒ S_xq=πrl=π.2.2√2=4√2 π

Đáp án cần chọn là:D

Câu 36. Một hình nón có đường kính đáy là 2a√3 , góc ở đỉnh là 120⁰. Tính thể tích của khối nón đó theo a.

A.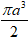  

B. πa³

C.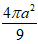 

D. 2πa³

Lời giải:

Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.

Theo giả thiết dễ suy ra đường tròn đáy có bán kính là:

 

Do góc ở đỉnh là 120⁰ nên 

Xét tam giác SAO vuông tại O, ta có:
SO =  = a

Do đó chiều cao hình nón là h = SO= a.

Vậy thể tích khối nón là
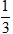
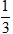
V =  πr²h =  π.3a².a = πa³

Đáp án cần chọn là:B

Câu 37. Một hình nón có đường sinh bằng 2a và diện tích xung quanh bằng 2πa² . Thể tích khối nón là:

A.     

B.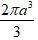  

C. 2πa³ 

D. √2πa³

Lời giải:

Ta có độ dài đường sinh là l = 2a .

Do diện tích xung quanh là 2πa² nên :

S_xq = π.R.l = 2πa² ⇒ R = 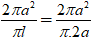 = a

Chiều cao của hình nón là:
h = 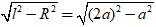 = √3a

Thể tích của khối nón là
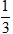
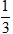
V =  πR²h =  π.a².√3 = 

Đáp án cần chọn là:A

Câu 38. Cắt hình nón (N) bằng một mặt phẳng đi qua trục của hình nón được thiết diện là một tam giác vuông cân có diện tích bằng 3a2. Diện tích xung quanh của (N) là:

A. 6πa²

B. √2πa²

C. 6√2πa² 

D. 3√2πa²

Lời giải:

Do cắt hình nón (N) bằng một mặt phẳng đi qua trục của hình nón nên thiết diện qua trục là mặt phẳng (SAB) – với AB là đường kính của đường tròn đáy.

Theo giả thiết tam giác SAB là tam giác vuông cân tại S và có diện tích 3a² nên

S_ABC =  SA² = 3a² ⇒ SA = √6a

Khi đó, độ dài đường sinh của hình nón là

l = SA = √6a

Do tam giác SAB là tam giác vuông cân tại S nên
AB = SA.√2 = √6a.√2 = 2√3a

Suy ra, đường cao của hình nón là:

h = SO = AB/2 = √3a

Bán kính đường tròn đáy là R = AB/2 = a√3 .

Diện tích xung quanh của (N) là:

S_xq = π.R.l = π.a√3.a.√6 = 3√2πa²

Đáp án cần chọn là:D

Câu 39. Thiết diện qua trục một hình nón là một tam giác vuông cân có cạnh huyền bằng 2√3 . Thể tích của khối nón này là

A. √3π

B. 3√3π

C. 3π

D. 3√2π

Lời giải:

+Gọi thiết diện qua trục là tam giác SAB, tâm đường tròn đáy là O. Khi đó, tam giác SAB có cạnh huyền

+ Xét tam giác SAB vuông cân tại S có SO là đường trung tuyến nên:

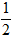
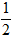
SO = AO =  AB =  2√3 = √3

⇒ Bán kính đường tròn đáy là: r = AO = √3 ; đường cao của hình nón là h = SO = √3

+Thể tích của hình nón là:

Đáp án cần chọn là:A

Câu 40. Cho hình nón có thiết diện qua đỉnh S tạo với đáy góc 60⁰ là tam giác đều cạnh bằng 4. Thể tích của khối nón đó là:

A. 9π

B. 4√3π

C. 3π

D. 7π

Lời giải:

+Gọi thiết diện qua đỉnh S là tam giác SAB, tâm đường tròn đáy là O.

+ Xác định góc giữa (SAB) và đáy:

Suy ra ((SAB);(O)) = (OH;SH) = 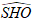 = 60⁰

+ Do tam giác SAB đều cạnh 4 nên SH = 2√3

+Xét tam giác SOH có

+Xét tam giác OAH có:

+ Thể tích hình nón đã cho là

Đáp án cần chọn là:D

Câu 41. Cho một hình cầu bán kính 5, cắt hình cầu này bằng một mặt phẳng sao cho thiết diện tạo thành là một đường kính 4. Tính thể tích của khối nón có đáy là thiết diện vừa tạo và đỉnh là tâm hình cầu đã cho. ( kết quả làm tròn tới hàng phần trăm).

A.18,18

B. 19,19

C. 19,2.

D. 17,16

Lời giải:

Gọi thiết diện là đường tròn tâm A, đường kính d= 4 ⇒ bán kính r = 2. Gọi MN là một đường kính của đường tròn (A).

Gọi O là tâm của mặt cầu đã cho.

Hình nón có đáy là thiết diện là hình tròn tâm A và đỉnh là O có:

• Bán kính đường tròn đáy là: r = 2.

• Đường sinh là OM = 5 ( = bán kính của hình cầu đã cho)

• Chiều cao:

Diện tích đường tròn đáy là: S = πr² = 4π

Thể tích khối nón cần tính là:

Đáp án cần chọn là:C

Câu 42. Hình chữ nhật ABCD có AB = 6; AD = 4. Gọi M, N, P, Q lần lượt là trung điểm bốn cạnh AB, BC, CD, DA. Cho hình chữ nhật ABCD quay quanh QN, tứ giác MNPQ tạo thành vật tròn xoay có thể tích bằng:

A. V = 8π

B. V = 6π

C. V = 4π

D. V = 2π

Lời giải:

Gọi O là tâm của hình chữ nhật ABCD, suy ra MNPQ là hình thoi tâm O.

Ta có:
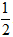
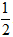
QO = ON =  AB = 3 và OM = OP =  AD = 2

Vật tròn xoay là hai hình nón bằng nhau có: đỉnh lần lượt là Q; N và chung đáy.

* Bán kính đáy OM = 2

* Chiều cao hình nón OQ = ON = 3

Vậy thể tích khối tròn xoay

Đáp án cần chọn là:A

Câu 43. Khẳng định nào sau đây là sai?

A. Có một mặt cầu đi qua các đỉnh của hình tứ diện bất kì.

B. Có một mặt cầu đi qua các đỉnh của một hình lăng trụ có đáy là một tứ giác lồi.

C. Có một mặt cầu đi qua các đỉnh của một hình hộp chữ nhật.

D. Có một mặt cầu đi qua các đỉnh của một hình chóp đều.

Lời giải:

Đáp án A: Đúng vì tứ diện là chóp tam giác, tam giác nội tiếp được đường tròn.

Đáp án B: Chưa chắc đúng vì tứ giác đó phải nội tiếp được đường tròn.

Đáp án C: Hình hộp chữ nhật có mặt cầu ngoại tiếp, tâm của nó là giao điểm của các đường chéo chính.

Đáp án D: Đúng vì đáy của hình chóp đều là đa giác đều thì luôn nội tiếp được đường tròn.

Đáp án cần chọn là:B

Câu 44. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và A’B’C’D’. Diện tích S là:

A. $$$\pi a^2$

B. $\pi a^2\sqrt{2}$

C. $\pi a^2\sqrt{3}$

D. $\frac{\pi a^2\sqrt{2}}{2}$

Lời giải:

Ta có bán kính đường tròn ngoại tiếp hình vuông ABCD là $r=OA=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}$

Vậy nên diện tích xung quanh của hình trụ là: $S_{xq}=2\pi r.l=2\pi .\frac{a\sqrt{2}}{2}.a=\pi a^2\sqrt{2}$

Đáp án cần chọn là:B

Câu 45. Gọi S là diện tích xung quanh của hình nón tròn xoay được sinh ra bởi đoạn thẳng AC’ của hình lập phương ABCD.A’B’C’D’ có cạnh b khi quay quanh trục AA’. Diện tích S là:

A. $$$\pi b^2$

B. $\pi b^2\sqrt{2}$

C. $\pi b^2\sqrt{3}$

D. $\pi b^2\sqrt{6}$

Lời giải:

Ta có, bán kính của đường tròn đáy là $A^{\prime }{C}^{\prime }=b\sqrt{2}.$ lúc này diện tích xung quanh của hình nón đã cho là

$A{C}^{\prime }=\sqrt{A{A}^{\prime 2}+A^{\prime }{B}^{\prime 2}+B^{\prime }{C}^{\prime 2}}=\sqrt{3b^2}=b\sqrt{3}$

$A^{\prime }{C}^{\prime }=b\sqrt{2}$

Ta có diện tích xung quanh của hình nón như sau:

$S_{xq}=\pi .r.l=\pi .A^{\prime }{C}^{\prime }.A{C}^{\prime }=\pi b\sqrt{2}.b\sqrt{3}=\pi b^2\sqrt{6}$

Đáp án cần chọn là:D

Câu 46. Hình chóp S.ABC có đáy là tam giác ABC vuông tại A, có SA vuông góc với (ABC) và có SA = a, AB = b và AC = c. Mặt cầu đi qua các đỉnh A, B, C, S có bán kính r bằng:

A. $$$\frac{2(a+b+c)}{3}$

B. $2\sqrt{a^2+b^2+c^2}$

C. $\frac{1}{2}\sqrt{a^2+b^2+c^2}$

D. $\sqrt{a^2+b^2+c^2}$

Lời giải:

Theo như hình ta gọi O là trung điểm của BC ⇒ O là tâm giao của đường tròn ngoại tiếp tam giác ABC. Đường thẳng Δ là trục của đường tròn tâm O.

Ta gọi I là giao điểm của mp trung trực của SA và Δ. Lúc này ta có I là tâm của mặt cầu đi qua A, B, C, S và r = IA.

Bán kính mặt cầu này ta có là

$r=IA=\sqrt{O{A}^2+I{O}^2}=\sqrt{(\frac{BC}{2}{)}^2+(\frac{SA}{2}{)}^2}$

$=\frac{1}{2}\sqrt{a^2+b^2+c^2}$

Đáp án cần chọn là:C

Câu 47. Cho hai điểm cố định A, B và một điểm M di động trong không gian nhưng luôn luôn thoả mãn điều kiện $$$\widehat{MAB}=\alpha$ với $0^0<\alpha <{90}^0$. Khi đó điểm M thuộc mặt nào trong các mặt sau:

A. Mặt nón

B. Mặt trụ

C. Mặt cầu

D. Mặt phẳng

Lời giải:

Sử dụng các khái niệm về các mặt tròn xoay. Ta có: $\widehat{MAB}=\alpha (0^0<\alpha <{90}^0$)

Vậy M thuộc mặt nón đỉnh là A, trục là đường thẳng AB và góc ở đỉnh bằng 2α.

Đáp án cần chọn là:A

Câu 48. Số mặt cầu chứa một đường tròn cho trước là:

A. 0

B. 1

C. 2

D. vô số

Lời giải:

Ta có vô số mặt cầu chứa một đường tròn cho trước nên chọn đáp án D nhé.

Có vô số mặt cầu chứa một đường tròn.

Đáp án cần chọn là:D

Câu 49. Trong các đa diện sau đây, đa diện nào không luôn luôn nội tiếp được trong mặt cầu:

A. Hình chóp tam giác (tứ diện);

B. Hình chóp ngũ giác đều;

C. Hình chóp tứ giác;

D. Hình hộp chữ nhật

Lời giải:

Ta có hình chóp tứ giác có đáy là hình bình hành thì không thể nào nội tiếp trong một mặt cầu vì đáy không thể nội tiếp đường tròn.

Đáp án cần chọn là:C

Câu 50. Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC) và cạnh BD vuông góc với cạnh BC. Khi quay các cạnh tứ diện đó quanh trục là cạnh AB, có bao nhiêu hình nón được tạo thành?

A. 1

B. 2

C. 3

D. 4

Lời giải:

Ta có đường thẳng AD ⊥ (ABC) suy ra AD ⊥ BC

Mặt khác ta có BC ⊥ BD

Vậy nên ta có: BC ⊥ AB

⇒ ΔABC vuông tại B cho nên cạnh AC quay quanh AB tạo thành một hình nón.

Tương tự ta có ΔABD là tam giác vuông tại A nên BD quay quanh AB tạo thành một hình nón.

Từ các suy luận trên ta có hai hình nón được tạo thành.

Đáp án cần chọn là:B