I. MẶT NÓN
1. Mặt nón tròn xoay
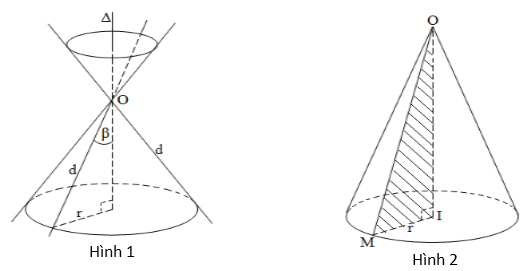
Trong mặt phẳng (P), cho 2 đường thẳng d, Δ cắt nhau tại O và chúng tạo thành góc β với 0o < β ≤ 90o . Khi quay mp(P) xung quanh trục Δ với góc β không thay đổi được gọi là mặt nón tròn xoay đỉnh O (hình 1).
- Người ta thường gọi tắt mặt nón tròn xoay là mặt nón.
- Đường thẳng Δ gọi là trục, đường thẳng d được gọi là đường sinh và góc 2β gọi là góc ở đỉnh.
2. Hình nón tròn xoay
Cho ΔOIM vuông tại I quay quanh cạnh góc vuông OI thì đường gấp khúc OIM tạo thành một hình, gọi là hình nón tròn xoay (gọi tắt là hình nón) (hình 2).
- Đường thẳng OI gọi là trục, O là đỉnh, OI gọi là đường cao và OM gọi là đường sinh của hình nón.
- Hình tròn tâm I, bán kính r = IM là đáy của hình nón.
3. Công thức diện tích hình nón và thể tích khối nón
Cho hình nón có chiều cao là h, bán kính đáy r và đường sinh là l thì có:
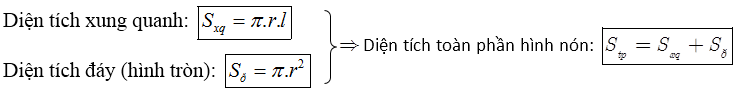
- Thể tích khối nón: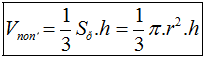 
.
4. Tính chất:
- TH1: Nếu cắt mặt nón tròn xoay bởi mp(P) đi qua đỉnh thì có các trường hợp sau xảy ra:
+ Nếu mp(P) cắt mặt nón theo 2 đường sinh ⇒ Thiết diện là tam giác cân.
+ Nếu mp(P) tiếp xúc với mặt nón theo một đường sinh. Trong trường hợp này, người ta gọi đó là mặt phẳng tiếp diện của mặt nón.
- TH2: Nếu cắt mặt nón tròn xoay bởi mp(Q) không đi qua đỉnh thì có các trường hợp sau xảy ra:
+ Nếu mp(Q) vuông góc với trục hình nón ⇒ giao tuyến là một đường tròn.
+ Nếu mp(Q) song song với 2 đường sinh hình nón giao tuyến là 2 nhánh của 1 hypebol.
+ Nếu mp(Q) song song với 1 đường sinh hình nón giao tuyến là 1 đường parabol.
II. MẶT TRỤ
1. Mặt trụ tròn xoay
Trong mp(P) cho hai đường thẳng Δ và l song song nhau, cách nhau một khoảng r. Khi quay mp(P) quanh trục cố định Δ thì đường thẳng l sinh ra một mặt tròn xoay được gọi là mặt trụ tròn xoay hay gọi tắt là mặt trụ.
- Đường thẳng Δ được gọi là trục.
- Đường thẳng l được gọi là đường sinh.
- Khoảng cách r được gọi là bán kính của mặt trụ.
2. Hình trụ tròn xoay
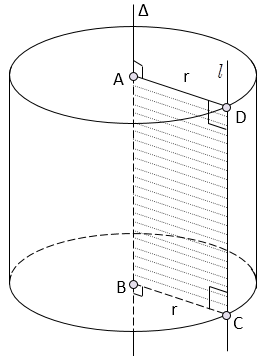
Khi quay hình chữ nhật ABCD xung quanh đường thẳng chứa một cạnh, chẳng hạn cạnh AB thì đường gấp khúc ABCD tạo thành một hình, hình đó được gọi là hình trụ tròn xoay hay gọi tắt là hình trụ.
- Đường thẳng AB được gọi là trục.
- Đoạn thẳng CD được gọi là đường sinh.
- Độ dài đoạn thẳng AB = CD = h được gọi là chiều cao của hình trụ.
- Hình tròn tâm A, bán kính r = AD và hình tròn tâm B, bán kính r = BC được gọi là 2 đáy của hình trụ.
- Khối trụ tròn xoay, gọi tắt là khối trụ, là phần không gian giới hạn bởi hình trụ tròn xoay kể cả hình trụ.
3. Công thức tính diện tích hình trụ và thể tích khối trụ
Cho hình trụ có chiều cao là và bán kính đáy bằng r, khi đó:
- Diện tích xung quanh của hình trụ: Sxq = 2πrh
- Diện tích toàn phần của hình trụ: Stp = Sxq + 2.SĐay = 2πrh + 2πr2
- Thể tích khối trụ: V = B.h = πr2h
4. Tính chất:
- Nếu cắt mặt trụ tròn xoay (có bán kính là r) bởi một mp(α) vuông góc với trục Δ thì ta được đường tròn có tâm trên α và có bán kính bằng r với r cũng chính là bán kính của mặt trụ đó.
- Nếu cắt mặt trụ tròn xoay (có bán kính là r) bởi một mp(α) không vuông góc với trục Δ nhưng cắt tất cả các đường sinh, ta được giao tuyến là một đường elíp có trụ nhỏ bằng 2r và trục lớn bằng 2r/sinφ, trong đó φ là góc giữa trục Δ và mp(α) với 00 < φ < 900.
- Cho mp(α) song song với trục Δ của mặt trụ tròn xoay và cách Δ một khoảng d.
+ Nếu d < r thì mp(α) cắt mặt trụ theo hai đường sinh ⇒ thiết diện là hình chữ nhật.
+ Nếu d = r thì mp(α) tiếp xúc với mặt trụ theo một đường sinh.
+ Nếu d > r thì mp(α) không cắt mặt trụ.
B. Bài tập trắc nghiệm
Câu 1: Tam giác ABC vuông cân đỉnh A có cạnh huyền là a. Quay tam giác ABC quanh trục AB thì đoạn gấp khúc ACB tạo thành hình nón (N). Diện tích xung quanh của hình nón (N) là:
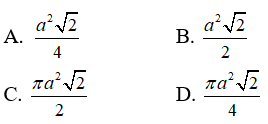
Theo cách xây dựng hình nón ta có đường sinh của hình nón là: l = BC = a .
Bán kính đáy của hình nón là: r = AC = BC.sin45o = a/√2
Vậy ta có diện tích xung quanh của hình nón (N) là:
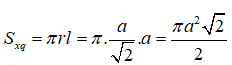
Đáp án đúng là C.
Câu 2: Hình nón (N) có đường sinh gấp hai lần bán kính đáy. Góc ở đỉnh của hình nón là :
A. 120o B. 60o C. 30o D. 0o
Từ giả thiết ta có l = 2r .
Gọi 2α là góc ở đỉnh của hình nón, khi đó ta có :
Vậy góc ở đỉnh của hình nón là 60o .
Đáp án đúng là B.
Câu 3: Hình nón có chiều cao bằng đường kính đáy. Tỉ số giữa diện tích xung quanh và diện tích toàn phần của hình nón bằng :
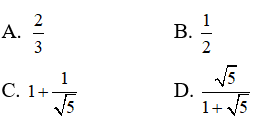
Từ giả thiết ta có:
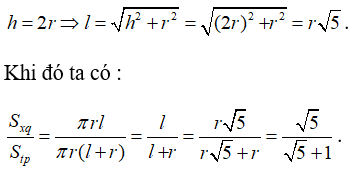
Đáp án đúng là D.
Câu 4: Một chiếc phễu đựng dầu hình nón có chiều cao là 30cm và đường sinh là 50cm. Giả sử rằng lượng dầu mà chiếc phễu đựng được chính là thể tích của khối nón. Khi đó trong các lượng dầu sau đây, lượng dầu nào lớn nhất chiếc phễu có thể đựng được :
A. 150720π(cm3) B. 50400π(cm3)
C. 16000π(cm3) D. 12000π(cm3)
Từ giả thiết ta có h = 30cm ; l = 50cm. Khi đó ta có
Thể tích khối nón là :
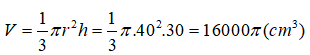
Đáp án đúng là C.
Câu 5: Cho hình trụ có được khi quay hình chữ nhật ABCD quanh trục AB. Biết rằng AB = 2AD = 2a. Thể tích khối trụ đã cho theo a là :
A. 2πa3 B.πa3 C. 2πa3 /3 D.πa3 /2
Từ giả thiết ta có h = AB = 2a, r = AD = a. Khi đó ta có thể tích khối trụ là: V = πr2h = 2πa3 .
Đáp án đúng là A.
Câu 6: Cho hình trụ có diện tích toàn phần là 7πa2 và bán kính đáy là a. Chiều cao của hình trụ là:
A. 3a/2 B. 2a C. 5a/3 D. 5a/2
Từ giả thiết ta có:
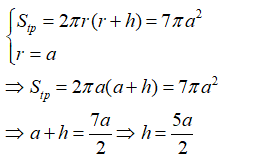
Đáp án đúng là D.
Câu 7: Để làm một thùng phi hình trụ người ta cần hai miếng nhựa hình tròn làm hai đáy có diện tích mỗi hình là 4π(cm2) và một miếng nhựa hình chữ nhật có diện tích là 15π(cm2) để làm thân. Tính chiều cao của thùng phi được làm.
A. 15/4(cm) B. 5(cm) C. 15/2(cm) D. 15(cm)
Diện tích miếng nhựa hình chữ nhật để làm thân bằng diện tích xung quanh của thùng phi.
Từ giả thiết ta có :
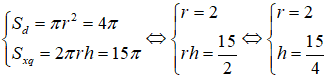
Đáp án đúng là A.
Câu 8: Cho hình chữ nhật ABCD có AB = 2AD. Lần lượt quay hình chữ nhật quanh các trục AB, AD ta được hai khối trụ lần lượt gọi là (H1), (H2). Tính tỉ số thể tích của khối trụ (H1) chia cho thể tích của khối trụ (H2)
A. 1 B. 1/4 C. 1/2 D. 2
Từ giả thiết ta có:
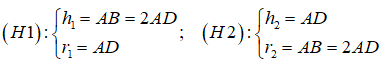
Khi đó ta có :
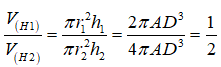
Đáp án đúng là C.
Câu 9: Cho hình trụ có bán kính đáy bằng a và diện tích toàn phần 6πa2. Diện tích của thiết diện của hình trụ cắt bởi mặt phẳng (P) đi qua các trục của hình trụ là :
A. a2 B. 2a2 C. 4a2 D. 6a2
Từ giả thiết ta có:
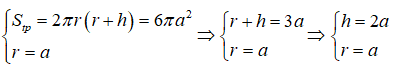
Thiết diện đã cho là một hình chữ nhật có các cạnh lần lượt là h và 2r. Khi đó ta có diện tích thiết diện là : S = 2rh = 4a2 .
Đáp án đúng là C.
Câu 10: Cho khối trụ có diện tích toàn phần là π và có thiết diện cắt bởi mặt phẳng đi qua trục là hình vuông. Thể tích khối trụ là :
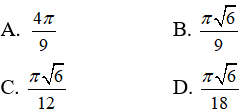
Từ giả thiết ta có:
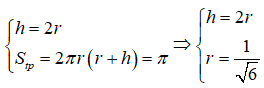
Thể tích khối trụ là :
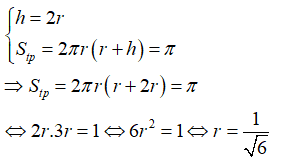
Đáp án đúng là D.
Câu 11:Cho hình chóp tứ giác đều S.ABCD có các cạnh bằng a√2 . Tính thể tích V của khối nón có đỉnh S và đường tròn đáy là đường tròn nội tiếp tứ giác ABCD?
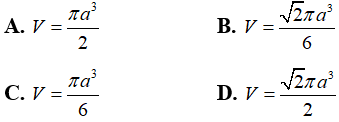
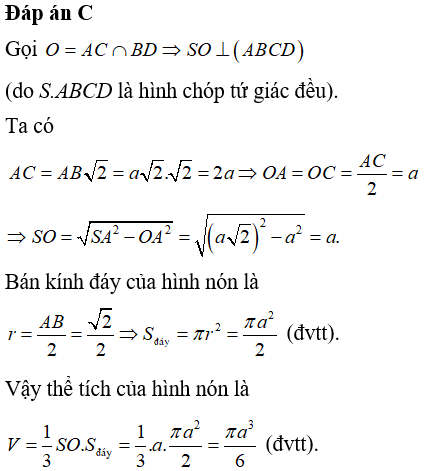
Câu 12:Cho hình nón S có chiều cao h = a và bán kính đáy r = 2a. Mặt phẳng (P) đi qua S và cắt đường tròn đáy tại A và B sao cho AB = 2√3a Tính khoảng cách d từ tâm của đường tròn đáy đến (P)
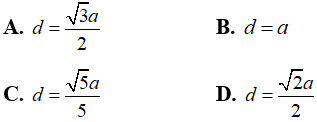
Câu 13: Cho khối nón tròn xoay có bán kính đáy r, đường sinh l và đường cao h. Công thức tính thể tích khối nón là:
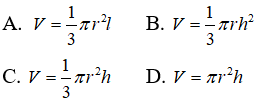
Theo công thức ta có đáp án đúng là C
Câu 14: Hình nón (N) có đường sinh gấp hai lần đường cao. Góc ở đỉnh của hình nón là:
A. 120o B. 90o C. 60o D. 30o
Gọi 2α là góc ở đỉnh của hình nón. Từ giả thiết ta có:
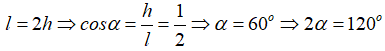
Câu 15: Hình nón có chiều cao bằng 4/3 bán kính đáy. Tỉ số giữa diện tích toàn phần và diện tích xung quanh của hình nón là:
A. 4/3 B. 5/7 C. 8/5 D. 9/5
Từ giả thiết ta có
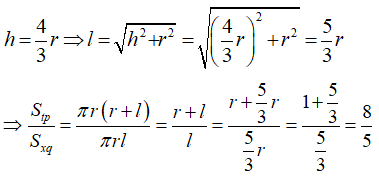
Câu 16: Hình nón có góc ở đỉnh là 90o và có diện tích xung quanh là π√2 . Độ dài đường cao của hình nón là:
A. 1 B. √2 C. 1/√2 D. 2
Câu 17: Cho hình nón tròn xoay có đường cao h=15cm và bán kính đáy r = 20cm. Diện tích xung quanh của hình nón là:
A. 1000π(cm2) B. 250π(cm2) C. 375π(cm2) D. 500π(cm2)
Từ giả thiết ta có :
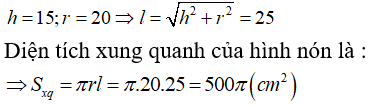
Câu 18: Cho khối nón tròn xoay có đường cao h = 20cm và đường sinh l = 25cm . Thể tích khối nón là:
A. 1500π(cm3) B. 2500π(cm3) C. 3500π(cm3) D. 4500π(cm3)
Từ giả thiết ta có:
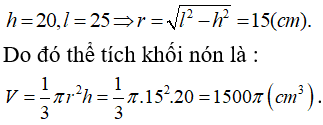
Câu 19: Tam giác ABC vuông đỉnh A có AB = 2AC. Quay tam giác ABC quanh trục AB thì đoạn gấp khúc ACB tạo ra hình nón (N1) và quay tam giác ABC quanh trục AC thì đoạn gấp khúc ABC tạo ra hình nón (N2). Tỉ số diện tích xung quanh của hình nón (N1) và diện tích xung quanh của hình nón (N2) là:
A. 1/4 B. 1/2 C. 1 D. 2
Đặt AC = a, ta có AB = 2a => BC = a√5 . Khi đó ta có :
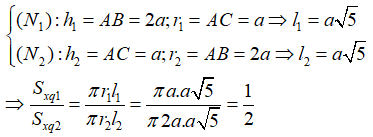
Câu 20: Cho khối nón tròn xoay có góc ở đỉnh là 60o và đường sinh l = 6cm. Thể tích của khối nón là:
A. 9π√3(cm3) B. 27π√3(cm3) C. 27π(cm3) D. 3π√3(cm3)
Từ giả thiết ta có:
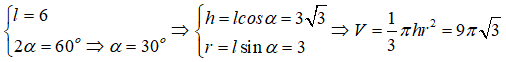
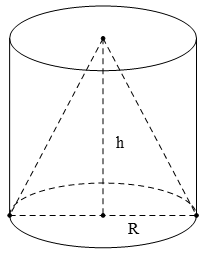
Câu 21: Cho một hình trụ có bán kính đáy R , chiều cao h và thể tích V1 ; một hình nón có đáy trùng với một đáy của hình trụ, có đỉnh trùng với tâm đáy còn lại của hình trụ (hình vẽ bên dưới) và có thể tích V2 .
Khẳng định nào sau đây là khẳng định đúng ?
A. V2 = 3V1
B. V1 = 2V2
C. V1 = 3V2
D. V2 = V1
Hình trụ có bán kính đáy R và chiều cao h nên thể tích V1 = πR2h .
Hình nón có bán kính đáy R và chiều cao h nên thể tích V2 = 1/3 πR2h .
Từ đó suy ra V1 = 3V2 .
Câu 22: Khối nón có góc ở đỉnh là 60o và có thể tích là π. Độ dài đường sinh của khối nón là:
Từ giả thiết ta có :
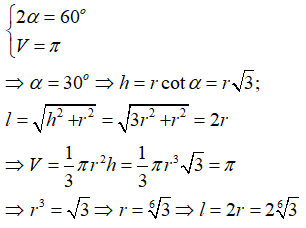
Câu 23: Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ một góc 45°. Tính thể tích của khối trụ.
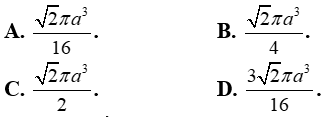
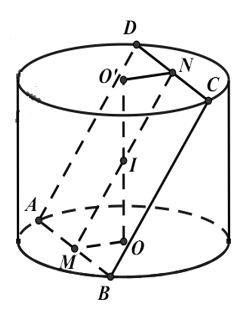
Gọi M, N lần lượt là trung điểm AB và CD.
Khi đó OM ⊥ AB và O’N ⊥ CD
Gọi I là giao điểm của MN và OO’
Đặt R = OA và h = OO’. Khi đó ΔIOM vuông cân tại O nên:
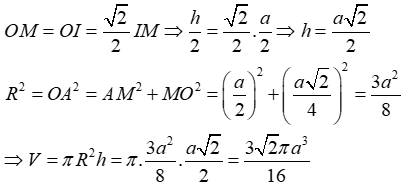
Câu 24: Cho khối trụ có bán kính đáy 4m và đường cao là 5m. Thể tích khối trụ là:
A. 20π(m3) B. 60π(m3) C. 80π(m3) D.100π(m3)
Từ giả thiết ta có: V = πr2h = π42.5 = 80π(m3)
Câu 25: Cho hình chữ nhật ABCD có AC = 2AD = 2a. Quay quanh trục AB đường gấp khúc ADCB ta được hình trụ có diện tích xung quanh là:
A. 6πa2 B. 3πa2 C. 2πa2√3 D. πa2√6
Từ giả thiết ta có : AC = 2AD = 2a suy ra:
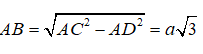
Khi đó ta có :
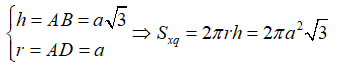
Câu 26:Tính thể tích của khối trụ biết chu vi đáy của hình trụ đó bằng 6π (cm) và thiết diện đi qua trục là một hình chữ nhật có độ dài đường chéo bằng 10 (cm).
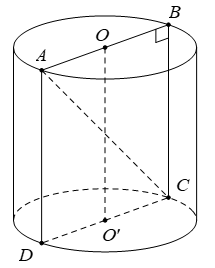
Gọi O, O' là hai tâm của đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD .
Do chu vi đáy của hình trụ đó bằng 6π nên bán kính đáy của hình trụ là
Câu 27: Cho hình trụ có diện tích toàn phần 6πa2 và thiết diện của hình trụ cắt bởi mặt phẳng (P) đi qua trục là một hình vuông. Chiều cao của hình trụ là:
A. 3a/4 B. a C. 3a/2 D. 2a
Vì thiết diện của hình trụ cắt bởi mặt phẳng (P) đi qua trục là một hình vuông nên: h = 2r
Câu 28: Cho hình trụ có diện tích toàn phần là 12π , đường cao của hình trụ là 1. Diện tích xung quanh của hình trụ là:
A. 6π B. 4π C. 2π D. π
Từ giả thiết ta có :
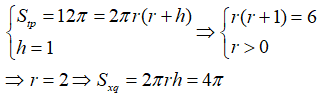
Câu 29: Cho hình trụ có chiều cao bằng 2a và diện tích xung quanh là πa2 . bán kính đáy của hình trụ là:
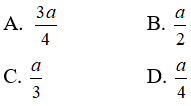
Từ giả thiết ta có:
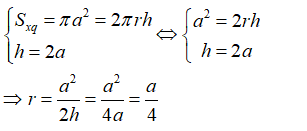
Câu 30: Cho khối trụ có diện tích toàn phần 5πa2 và bán kính đáy là a. Thể tích khối trụ là:
A. 3πa3/2 B. πa3/2 C. πa3 D. 3πa3
Từ giả thiết ta có:
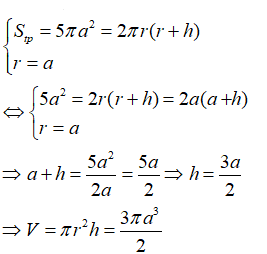
Câu 31: Hình trụ (H) có diện tích toàn phần là 8π(cm2) và thể tích khối trụ là 3π(cm3) . Tính chiều cao của hình trụ ta được bao nhiêu kết quả?
A. 1 B. 2 C. 3 D. 4
Từ giả thiết ta có:
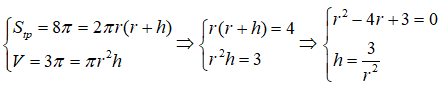
Do r > 0 nên ta có 2 giá trị r thỏa mãn hay có hai hình nón thỏa mãn đề bài
Câu 32: Hình trụ (H) có tỉ số diện tích xung quanh và diện tích toàn phần là 1/3 . Biết rằng thể tích khối trụ là 4π . Bán kính đáy của hình trụ là:
A. 2 B. 3 C. √6 D. √7
Từ giả thiết ta có:
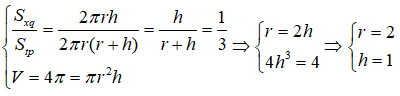
Câu 33: Ta dùng hai hình chữ nhật có cùng kích cỡ để làm thành hai hình trụ (H1) và (H2) bằng cách quay các hình chữ nhật đó, lần lượt theo chiều dài và chiều rộng. Tỉ số hai diện tích xung quanh hình trụ (H1) và hình trụ (H2) là:
A. 2 B. 1 C. 1/2 D. 1/4
Gọi chiều dài và chiều rộng của hình chữ nhật là a và b.
Hình trụ (H1) có r1 = a ; h1 = b
Hình trụ (H2) có r2 = b ; h2= a
Ta có: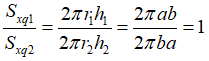 
Câu 34: Cho hình nón có đường cao h = 10cm và thiết diện cắt bởi mặt phẳng qua trục của hình nón là một tam giác đều. Diện tích xung quanh của hình nón là:
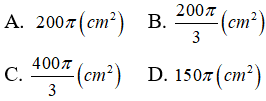
Từ giả thiết ta có thiết diện là tam giác đều cạnh 2r và đường cao h nên ta có :
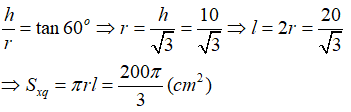
Câu 35: Một hình nón có đường sinh bằng đường kính đáy. Diện tích xung quanh của hình nón bằng 9π . Tính đường cao h của hình nón.
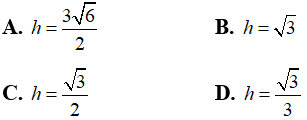
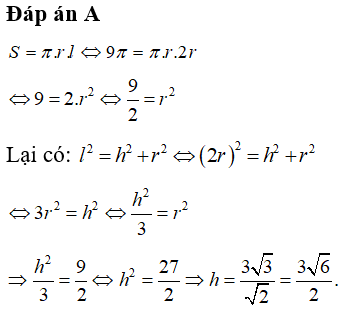
Câu 36: Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và đáy bằng 60° . Tính diện tích xung quanh Sxq của hình nón đỉnh S có đáy là hình tròn ngoại tiếp tam giác ABC.
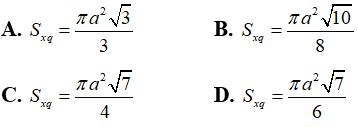
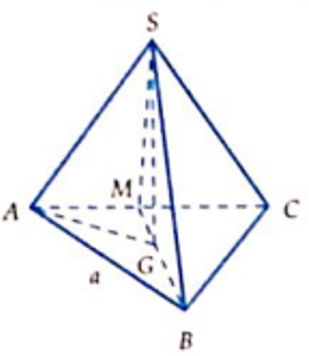
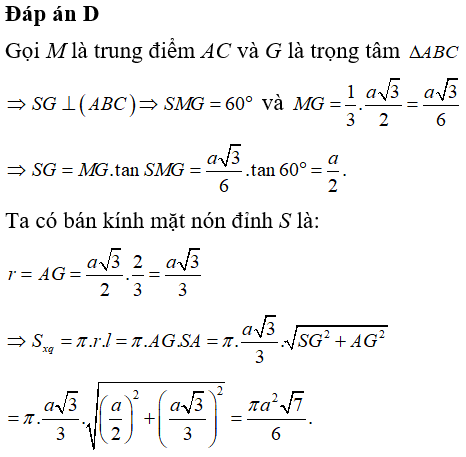
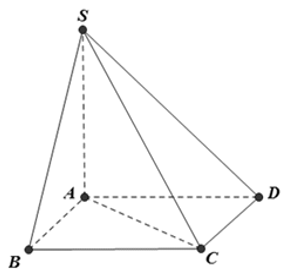
Câu 37: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy SC = a√6 . Khi tam giác SAC quay quanh cạnh SA thì đường gấp khúc SAC tạo thành một hình nón tròn xoay. Thể tích của khối nón tròn xoay đó là:
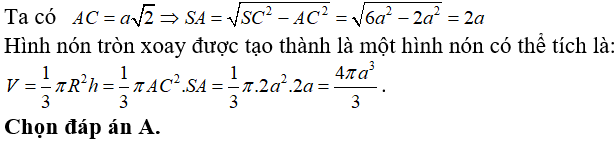
Câu 38: Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = AD = a, AB' = 2a . Diện tích toàn phần của hình trụ ngoại tiếp hình hộp là:
A. πa2(1 + √6) B. πa2(1 + √3) C. πa2(1 + √2) D. 2πa2
Xét tam giác vuông ABB’ ta có:
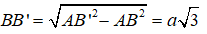
Hình trụ ngoại tiếp hình hộp đã cho có chiều cao h = AA’= BB’
Đáy hình trụ là đường tròn ngoại tiếp tứ giác ABCD và A’B’C’D’
Ta có :
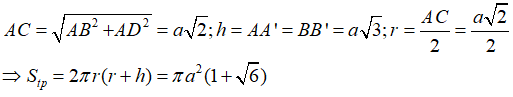
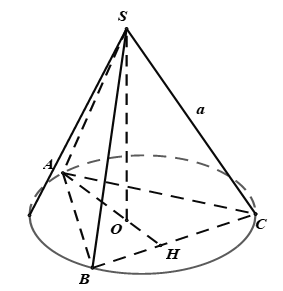
Câu 39: Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng 2 và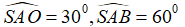 
;. Tính diện tích xung quanh hình nón ?
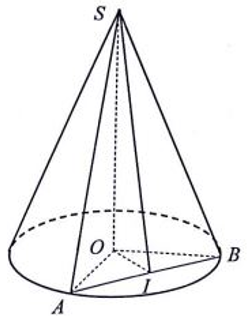
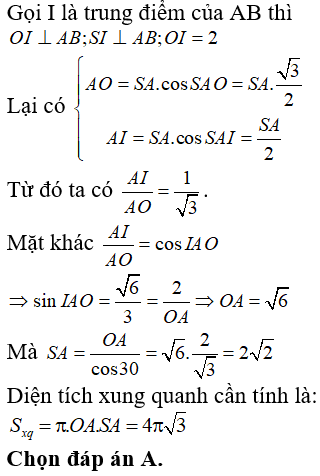
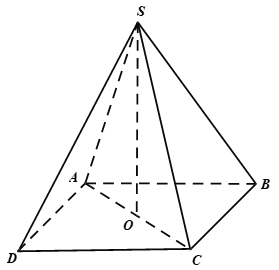
Câu 40: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, góc ∠SAB = 60° . Thể tích của hình nón đỉnh S đáy là đường tròn ngoại tiếp ABCD là:
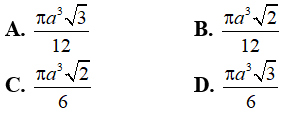
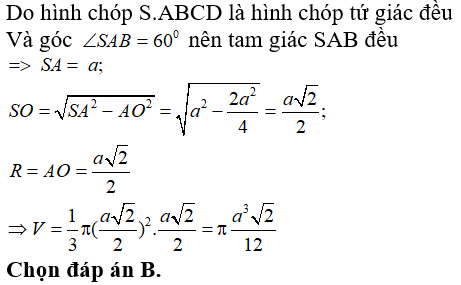
Câu 41: Hình nón tròn xoay ngoại tiếp tứ diện đều cạnh a, có diện tích xung quanh là:
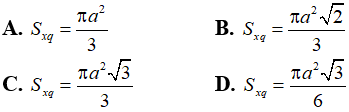
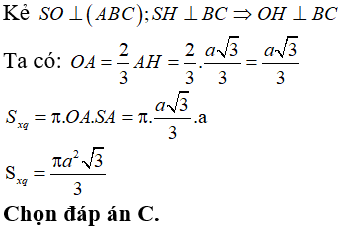
Câu 42: Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích xung quanh của hình nón bằng
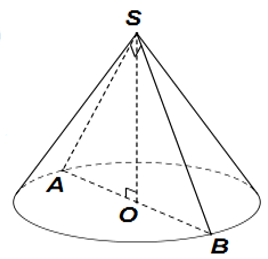
Giả sử SAB là thiết diện qua trục của hình nón (như hình vẽ)
Tam giác SAB cân tại S và là tam giác cân nên SA = SB = a
Do đó:
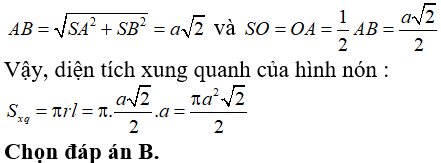
Câu 43: Cho hình nón S, đường cao SO. Gọi A, B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng a và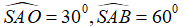 
. Tính diện tích xung quanh hình nón.
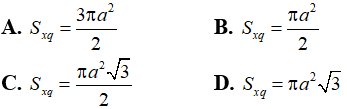
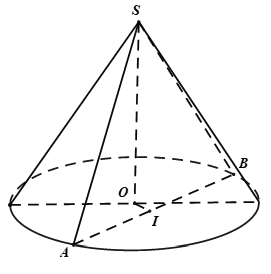
Câu 44: Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính diện tích xung quanh và thể tích của hình nón có đỉnh S và đáy là đường tròn ngoại tiếp đáy hình chóp S.ABCD. Khi đó diện tích xung quanh và thể tích của hình nón bằng
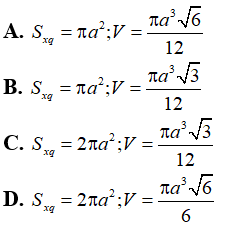
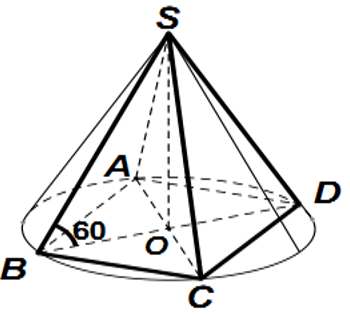
Gọi O là tâm của hình vuông ABCD.
Do S.ABCD là hình chóp đều nên SO ⊥ (ACBD)
Suy ra, OB là hình chiếu vuông góc của SB lên mp(ABCD)
Câu 45: Một người xây nhà phải xây bốn cái cột hình trụ cùng kích cỡ, bán kính đáy các cột là 25cm. Biết rằng tổng thể tích vật liệu (chính là tổng thể tích bốn khối trụ) là 3m3. Chiều cao của mỗi cột là:
Từ giả thiết đề bài ta có tổng thể tích của bốn khối trụ là 3m3 và bán kính đáy của mỗi khối trụ là r = 25cm = 0,25m.
Gọi h là chiều cao của các khối trụ ta có :
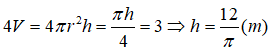
Câu 46: Một hộp đứng bóng bàn hình trụ có chiều cao 30cm, bán kính 2,5cm. Vận động viên để các quả bóng bàn có bán kính 2,5cm vao hộp. Hỏi vận động viên có thể để được nhiều nhất bao nhiêu quả bóng bàn trong các kết quả sau?
A. 3 B. 6 C. 12 D. 15
Do bán kính của một quả bóng bàn hình cầu bằng bán kính hình trụ nên mỗi lần ta chỉ đặt được một quả bóng bàn vào hình trụ. Khi đó do mỗi quả bóng bàn chiếm chiều cao là 2,5x2=5cm nên với hình trụ cao 30cm thì đựng được nhiều nhất là 6 quả bóng bàn
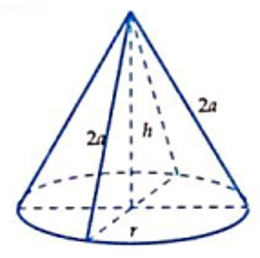
Câu 47: Một hình nón có độ dài đường sinh bằng 2a và mặt phẳng qua trục cắt hình nón theo thiết diện là tam giác vuông. Tính thể tích V của khối nón.
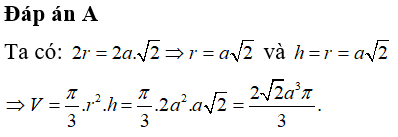
Câu 48: Cho hình trụ có bán kính đáy 10cm và đường cao là 15cm. ta để một thước thẳng có chiều dài l vào trong hình trụ. Khi đó trong các kết quả sau l có thể nhận giá trị lớn nhất là:
A. 30 (cm) B. 24 (cm) C. 20(cm) D. 15(cm)
Để một chiếc thước thẳng có thể nằm trong một hình trụ thì độ dài của nó không thể vượt quá được độ dài đường chéo của hình chữ nhật là thiết diện của hình trụ cắt bởi mặt phẳng qua trục của hình trụ. Do đó độ dài thước không vượt quá :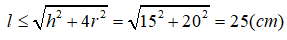 
Câu 49: Cho lăng trụ đứng ABCD.A'B'C'D có đáy ABCD là hình thang, AB = AD = a, CD = 2a. Đường thẳng A’C tạo với mặt phẳng (ABCD) một góc bằng 60o . Biết hình lăng trụ nội tiếp một hình trụ. Tính thể tích khối trụ ngoại tiếp lăng trụ theo a ta được:
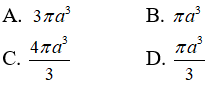
Từ giả thiết ta có hình thang ABCD là hình thang nội tiếp được đường tròn nên nó là hình thang cân AB = AD = BC = a
Khi đó tâm đường tròn ngoại tiếp hình thang ABCD là trung điểm I của CD và bán kính là r = a .
Ta có:
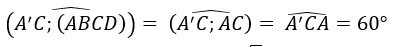
=> A'A = a√3√3 = 3a => V = 3πa3
Câu 50: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt phẳng qua AB và trung điểm M của SC cắt hình chóp theo một thiết diện có chu vi bằng 7a. Thể tích khối nón có đỉnh S và đường tròn đáy ngoại tiếp ABCD là:
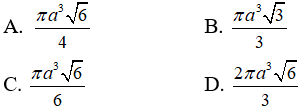
Do AB // CD nên mặt phẳng (ABM) cắt mặt phẳng (SCD) theo một giao tuyến đi qua M và song song với CD, giao tuyến đó cắt SD tại N. Suy ra N là trung điểm của SD. Từ giả thiết ta có :
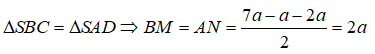
Áp dụng công thức đường trung tuyến trong tam giác SBC ta có :
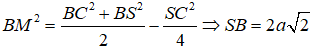
Khối nón đã cho có :
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.
