Toptailieu.vn biên soạn và giới thiệu lời giải Toán 11 (Chân trời sáng tạo) Bài tập cuối chương 6 trang 34 hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi sgk Toán 11 Bài tập cuối chương 6 trang 34 từ đó học tốt môn Toán 11.

Toán 11 (Chân trời sáng tạo) Bài tập cuối chương 6 trang 34

Giải Toán 11 trang 34 Tập 2

Câu hỏi trắc nghiệm

Bài 1 trang 34 Toán 11 Tập 2: Rút gọn biểu thức 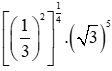, ta được

A. $\sqrt{3}$.

B. $3\sqrt{3}$.

C. $\frac{1}{\sqrt{3}}$.

D. 9.

Lời giải:

Đáp án đúng là: D

$=3^{-\frac{1}{2}}.3^{\frac{5}{2}}=3^{-\frac{1}{2}+\frac{5}{2}}=3^2=9$.

Bài 2 trang 34 Toán 11 Tập 2: Nếu 2^α = 9 thì ${\left(\frac{1}{16}\right)}^{\frac{\alpha }{8}}$ có giá trị bằng

A. $\frac{1}{3}$.

B. 3.

C. $\frac{1}{9}$.

D. $\frac{1}{\sqrt{3}}$.

Lời giải:

Đáp án đúng là: A

${\left(\frac{1}{16}\right)}^{\frac{\alpha }{8}}={\left(2^{-4}\right)}^{\frac{\alpha }{8}}=2^{-4.\frac{\alpha }{8}}=2^{-\frac{1}{2}\alpha }$

$={\left(2^{\alpha }\right)}^{-\frac{1}{2}}=9^{-\frac{1}{2}}=\frac{1}{3}$.

Bài 3 trang 34 Toán 11 Tập 2: Nếu $a^{\frac{1}{2}}=b\left(a>0,a\ne 1\right)$ thì

A. ${\log }_{\frac{1}{2}}a=b$.

B. $2{\log }_{a}b=1$.

C. ${\log }_a\frac{1}{2}=b$.

D. ${\log }_{\frac{1}{2}}b=a$.

Lời giải:

Đáp án đúng là: B

$a^{\frac{1}{2}}=b\iff {\log }_{a}b=\frac{1}{2}\iff 2{\log }_{a}b=1$.

Bài 4 trang 34 Toán 11 Tập 2: Nếu $x={\log }_{3}4+{\log }_{9}4$ thì 3^x có giá trị bằng

A. 6.

B. 8.

C. 16.

D. 64.

Lời giải:

Đáp án đúng là: B

Ta có $x={\log }_{3}4+{\log }_{9}4={\log }_{3}4+{\log }_{3^2}4$

$={\log }_{3}4+\frac{1}{2}{\log }_{3}4={\log }_{3}4+{\log }_3{4}^{\frac{1}{2}}$

$={\log }_{3}4+\frac{1}{2}{\log }_{3}4={\log }_{3}4+{\log }_{3}2$

$={\log }_3\left(4.2\right)={\log }_{3}8$

⇔ 3^x = 8.

Bài 5 trang 34 Toán 11 Tập 2: Cho α, β là hai số thực với α < β. Khẳng định nào sau đây đúng ?

A. ${\left(\mathrm{0,3}\right)}^{\alpha }<{\left(\mathrm{0,3}\right)}^{\beta }$.

B. ${\pi }^{\alpha }\ge {\pi }^{\beta }$.

C. ${\left(\sqrt{2}\right)}^{\alpha }<{\left(\sqrt{2}\right)}^{\beta }$.

D. ${\left(\frac{1}{2}\right)}^{\beta }>{\left(\frac{1}{2}\right)}^{\alpha }$.

Lời giải:

Đáp án đúng là: C

• Xét phương án A.

Do 0 < 0,3 < 1 nên hàm số y = 0,3^x nghịch biến trên ℝ.

Mà α < β nên (0,3)^α < (0,3)^β.

• Xét phương án B.

Do π > 1 nên hàm số y = π^x đồng biến trên ℝ.

Mà α < β nên π^α < π^β.

• Xét phương án C.

Do $\sqrt{2}>1$ nên hàm số $y={\left(\sqrt{2}\right)}^x$ đồng biến trên ℝ.

Mà α < β nên ${\left(\sqrt{2}\right)}^{\alpha }<{\left(\sqrt{2}\right)}^{\beta }$.

• Xét phương án D.

Do $0<\frac{1}{2}<1$ nên hàm số $y={\left(\frac{1}{2}\right)}^x$ đồng biến trên ℝ.

Mà α < β nên${\left(\frac{1}{2}\right)}^{\alpha }<{\left(\frac{1}{2}\right)}^{\beta }\iff {\left(\frac{1}{2}\right)}^{\beta }>{\left(\frac{1}{2}\right)}^{\alpha }$.

Bài 6 trang 34 Toán 11 Tập 2: Hình nào vẽ đồ thị của hàm số $y={\log }_{\frac{1}{2}}x$?

A. 

B. 

C. 

D. 

Lời giải:

Đáp án đúng là: D

− Hàm số $y={\log }_{\frac{1}{2}}x$nghịch biến trên (0; +∞). Loại A, C.

− Giới hạn: $\underset{x\to +\infty }{\lim }{\log }_{\frac{1}{2}}x=-\infty ;\underset{x\to 0^{+}}{\lim }{\log }_{\frac{1}{2}}x=+\infty$. Loại B.

Bài 7 trang 34 Toán 11 Tập 2: Phương trình ${\mathrm{0,1}}^{2x-1}=100$ có nghiệm là

A. $-\frac{1}{2}$.

B. $\frac{1}{3}$.

C. $1\frac{1}{2}$.

D. $2\frac{1}{3}$.

Lời giải:

Đáp án đúng là: A

${\mathrm{0,1}}^{2x-1}=100\iff {\mathrm{0,1}}^{2x-1}={\mathrm{0,1}}^{-2}\iff 2x-1=-2$

$\iff 2x=-1\iff x=-\frac{1}{2}$.

Bài 8 trang 34 Toán 11 Tập 2: Tập nghiệm của bất phương trình 0,5^3x1>0,25 là

A. (−∞; 1).

B. (1; +∞).

C. (0; 1).

D. $\left(-\infty ;-\frac{1}{3}\right)$.

Lời giải:

Đáp án đúng là: A

0,5^3x−1>0,25⇔0,5^3x−1>0,5²

⇔3x−1<2(do 0<0,5<1)

⇔3x<3⇔x<1.

Vậy tập nghiệm của bất phương trình là (−∞;1).

Bài 9 trang 34 Toán 11 Tập 2: Nếu $\log x=2\log 5-\log 2$ thì

A. x = 8.

B. x = 23.

C. x = 12,5.

D. x = 5.

Lời giải:

Đáp án đúng là: C

ĐKXĐ: x > 0

Khi đó: $\log x=2\log 5-\log 2\iff \log x=\log 5^2-\log 2$

$\iff \log x=\log \frac{25}{2}\iff x=\frac{25}{2}=\mathrm{12,5}$.

Bài 10 trang 34 Toán 11 Tập 2: Số nguyên dương nhỏ nhất thỏa mãn ${\log }_{\mathrm{0,1}}\left(1-2x\right)>-1$ là

A. x = 0.

B. x = 1.

C. x = −5.

D. x = −4.

Lời giải:

Đáp án đúng là: D

ĐKXĐ: $1-2x>0\iff x<\frac{1}{2}$.

Khi đó: ${\log }_{\mathrm{0,1}}\left(1-2x\right)>-1\iff 1-2x<{\mathrm{0,1}}^{-1}$

$\iff 1-2x<10\iff -2x<9\iff x>-\frac{9}{2}.$

Kết hợp với điều kiện ta được nghiệm của bất phương trình là $-\frac{9}{2}<x<\frac{1}{2}.$

Vậy số nguyên x nhỏ nhất thỏa mãn ${\log }_{\mathrm{0,1}}\left(1-2x\right)>-1$ là x = − 4.

Giải Toán 11 trang 35 Tập 2

Bài tập tự luận

Bài 11 trang 35 Toán 11 Tập 2: Biết 4^α + 4^−α = 5. Tính giá trị biểu thức :

a )2^α + 2^−α;

b )4^2α + 4^−2α .

Lời giải:

a) Ta có ${\left(2^{\alpha }+2^{-\alpha }\right)}^2={\left(2^{\alpha }\right)}^2+2.2^{\alpha }.2^{-\alpha }+{\left(2^{-\alpha }\right)}^2$

$={\left(2^2\right)}^{\alpha }+2+{\left(2^2\right)}^{-\alpha }=4^{\alpha }+2+4^{-\alpha }$

$=\left(4^{\alpha }+4^{-\alpha }\right)+2=5+2=7$.

Vậy $2^{\alpha }+2^{-\alpha }=\sqrt{7}$.

b) Ta có $4^{2\alpha }+4^{-2\alpha }={\left(4^{\alpha }\right)}^2+{\left(4^{-\alpha }\right)}^2$

$={\left(4^{\alpha }\right)}^2+2.4^{\alpha }.4^{-\alpha }+{\left(4^{-\alpha }\right)}^2-2.4^{\alpha }.4^{-\alpha }$

$={\left(4^{\alpha }+4^{-\alpha }\right)}^2-2=5^2-2=23$.

Vậy $4^{2\alpha }+4^{-2\alpha }=23$.

Bài 12 trang 35 Toán 11 Tập 2: Tính giá trị của biểu thức :

a) ${\log }_{2}72-\frac{1}{2}\left({\log }_{2}3+{\log }_{2}27\right)$;

b) $5^{{\log }_{2}40-{\log }_{2}5}$;

c) $3^{2+{\log }_{9}2}$.

Lời giải:

a )${\log }_{2}72-\frac{1}{2}\left({\log }_{2}3+{\log }_{2}27\right)={\log }_{2}72-\frac{1}{2}{\log }_2\left(3.27\right)$

$={\log }_{2}72-\frac{1}{2}{\log }_{2}81={\log }_{2}72-{\log }_2{81}^{\frac{1}{2}}$

$={\log }_{2}72-{\log }_{2}9={\log }_2\frac{72}{9}={\log }_{2}8$

$={\log }_2{2}^3=3{\log }_{2}2=3$;

b) $5^{{\log }_{2}40-{\log }_{2}5}=5^{{\log }_2\frac{40}{5}}=5^{{\log }_{2}8}=5^{{\log }_2{2}^3}$

$=5^{3{\log }_{2}2}=5^3=125$;

c) $3^{2+{\log }_{9}2}=3^{{\log }_9{9}^2+{\log }_{9}2}=3^{{\log }_9\left(9^2.2\right)}=3^{{\log }_{3^2}\left(9^2.2\right)}$

$=3^{\frac{1}{2}{\log }_3\left(9^2.2\right)}={\left(3^{{\log }_3\left(9^2.2\right)}\right)}^{\frac{1}{2}}={\left(9^2.2\right)}^{\frac{1}{2}}=9\sqrt{2}$.

Bài 13 trang 35 Toán 11 Tập 2: Biết rằng 5^x = 3 và 3^y = 5. Không sử dụng máy tính cầm tay, tính giá trị của xy.

Lời giải:

Ta có 5^x = 3 ⇔ x = log₅ 3 và 3^y = 5 ⇔ y = log₃ 5.

Do đó $xy=lo{g}_{5}3.lo{g}_{3}5=lo{g}_{5}3.\frac{1}{lo{g}_{5}3}=1$.

Bài 14 trang 35 Toán 11 Tập 2: Viết công thức biểu thị y theo x, biết

$2{\log }_{2}y=2+\frac{1}{2}{\log }_{2}x$.

Lời giải:

Ta có $2{\log }_{2}y=2+\frac{1}{2}{\log }_{2}x$

$\iff {\log }_2{y}^2={\log }_2{2}^2+{\log }_2{x}^{\frac{1}{2}}$

$\iff {\log }_2{y}^2={\log }_2\left(2^2.x^{\frac{1}{2}}\right)$

$\iff y^2=2^2.x^{\frac{1}{2}}\iff y=2\sqrt[4]{x}$.

Bài 15 trang 35 Toán 11 Tập 2: Giải các phương trình sau:

a)${\left(\frac{1}{4}\right)}^{x-2}=\sqrt{8}$;

b)$9^{2x-1}=81.{27}^x$;

c) $2{\log }_5\left(x-2\right)={\log }_{5}9$;

d)${\log }_2\left(3x+1\right)=2-{\log }_2\left(x-1\right)$.

Lời giải:

a)${\left(\frac{1}{4}\right)}^{x-2}=\sqrt{8}\iff {\left({\left(\frac{1}{2}\right)}^2\right)}^{x-2}=8^{\frac{1}{2}}$

$\iff {\left(\frac{1}{2}\right)}^{2\left(x-2\right)}={\left({\left(\frac{1}{2}\right)}^{-3}\right)}^{\frac{1}{2}}\iff {\left(\frac{1}{2}\right)}^{2x-4}={\left(\frac{1}{2}\right)}^{-\frac{3}{2}}$

$\iff 2x-4=-\frac{3}{2}\iff 2x=\frac{5}{2}\iff x=\frac{5}{4}$.

Vậy phương trình đã cho có nghiệm $x=\frac{5}{4}$.

b)$9^{2x-1}=81.{27}^x\iff {\left(3^2\right)}^{2x-1}=3^4.{\left(3^3\right)}^x$

$\iff 3^{4x-2}=3^{3x+4}\iff 4x-2=3x+4$

$\iff 4x-2=3x+4\iff 4x-3x=2+4\iff x=6$

Vậy phương trình đã cho có nghiệm x = 6.

c) ĐKXĐ: x – 2 > 0 ⇔ x > 2.

Khi đó: $2{\log }_5\left(x-2\right)={\log }_{5}9\iff {\log }_5{\left(x-2\right)}^2={\log }_5{3}^2$

Vậy phương trình đã cho có nghiệm x = 5.

d)ĐKXĐ: 

Khi đó: ${\log }_2\left(3x+1\right)=2-{\log }_2\left(x-1\right)$

$\iff {\log }_2\left(3x+1\right)+{\log }_2\left(x-1\right)=2$

$\iff {\log }_2\left(3x^2-2x-1\right)={\log }_{2}4$

$\iff 3x^2-2x-1=4\iff 3x^2-2x-5=0$

Vậy phương trình đã cho có nghiệm $x=\frac{5}{3}$.

Bài 16 trang 35 Toán 11 Tập 2: Giải các bất phương trình :

a)${\left(\frac{1}{9}\right)}^{x+1}>\frac{1}{81}$;

b) ${\left(\sqrt[4]{3}\right)}^x\le 27.3^x$;

c)${\log }_2\left(x+1\right)\le {\log }_2\left(2-4x\right)$.

Lời giải:

a)${\left(\frac{1}{9}\right)}^{x+1}>\frac{1}{81}\iff {\left(\frac{1}{9}\right)}^{x+1}>{\left(\frac{1}{9}\right)}^2$

$\iff x+1<2$(do $0<\frac{1}{9}<1$)

$\iff x<1$

Vậy bất phương trình đã cho có nghiệm x < 1.

b) ${\left(\sqrt[4]{3}\right)}^x\le 27.3^x\iff {\left(3^{\frac{1}{4}}\right)}^x\le 3^3.3^x$

$\iff 3^{\frac{x}{4}}\le 3^{3+x}\iff \frac{x}{4}\le 3+x$(do 3 > 1)

$\iff x\ge -4$.

Vậy bất phương trình đã cho có nghiệm $x\ge -4$.

c)ĐKXĐ: 

Khi đó: ${\log }_2\left(x+1\right)\le {\log }_2\left(2-4x\right)$

$\iff x+1\le 2-4x\iff 5x\le 1\iff x\le \frac{1}{5}$.

Kết hợp với điều kiện ta được nghiệm của bất phương trình $-1<x\le \frac{1}{5}$.

Bài 17 trang 35 Toán 11 Tập 2: Thực hiện một mẻ nuôi cấy vi khuẩn với 1000 vi khuẩn ban đầu, nhà sinh học phát hiện số lượng vi khuẩn tăng thêm 25% sau mỗi hai ngày.

a) Công thức P(t) = P₀.a^t cho phép tính số lượng vi khuẩn của mẻ nuôi cấy sau t ngày kể từ thời điểm ban đầu. Xác định các tham số P₀ và a (a > 0). Làm tròn a đến hàn phần trăm.

b) Sau 5 ngày thì số lượng vi khuẩn bằng bao nhiêu? Làm tròn kết quả đến hàng trăm.

c) Sau bao nhiêu ngày thì số lượng vi khuẩn vượt gấp đôi số lượng ban đầu? Làm tròn kết quả đến hàng phần mười.

Lời giải:

a) Ban đầu có 1000 vi khuẩn nên P₀=1000.

Sau 2 ngày, số lượng vi khuẩn là:

P=125% . P₀=125%.1000=1250

Ta có:P(2)=P₀.a²⇔1250=1000.a²

⇔a²=1,25⇔a≈1,12.

b) Số lượng vi khuẩn sau 5 ngày là:

P(5)=P₀.a⁵=1000.1,122≈1800(vi khuẩn).

c) Với P(t)=2P₀, ta có:

P(t)=P₀.a^t⇔2P₀=P₀.1,12^t

⇔1,12^t=2⇔t=log_1,122≈6,1(ngày)

Vậy sau 6,1 ngày thì số lượng vi khuẩn vượt gấp đôi số lượng ban đầu.

Bài 18 trang 35 Toán 11 Tập 2: Nhắc lại rằng, độ pH của một dung dịch được tính theo công thức pH = −log [H⁺], trong đó [H⁺] là nồng độ H⁺ của dung dịch đó tính bằng mol/L. Nồng độ H⁺ trong dung dịch cho biết độ acid của dung dịch đó.

a) Dung dịch acid A có độ pH bằng 1,9; dung dịch B có độ pH bằng 2,5. Dung dịch nào có độ acid cao hơn và cao hơn bao nhiêu lần?

b) Nước cất có nồng độ H⁺ là 10^–7 mol/L. Nước chảy từ một vòi nước có độ pH từ 6,5 đến 6,7 thì có độ acid cao hay thấp hơn nước cất.

Lời giải:

a)• pH_A=1,9⇔−log[H⁺]=1,9

⇔log[H⁺]=−1,9⇔H⁺=10^−1,9.

Vậy độ acid của dung dịch A là 10^−1,9 mol/L.

• pH_B=2,5⇔−log[H⁺]=2,5

⇔log[H⁺]=−2,5⇔H⁺=10^−2,5.

Vậy độ acid của dung dịch B là 10^−2,5mol/L.

Ta có: $\frac{{10}^{-\mathrm{1,9}}}{{10}^{-\mathrm{2,5}}}\approx \mathrm{3,98}$.

Vậy độ acid của dung dịch A cao hơn độ acid của dung dịch B 3,98 lần.

b) Ta có:6,5<pH<6,7⇔6,5<−log[H⁺]<6,7

⇔−6,5>log[H⁺]>−6,7⇔10^−6,5>H⁺>10^−6,7.

Do đó nước chảy từ vòi nước có độ acid từ 10^−6,7mol/L đến 10^−6,5mol/L.

Vậy nước đó có độ acid cao hơn nước cất.

Xem thêm Lời giải bài tập Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 4: Phương trình, bất phương trình mũ và lôgarit

Bài 1: Đạo hàm

Bài 2: Các quy tắc tính đạo hàm

Bài tập cuối chương 7 trang 51

Bài 1: Hai đường thẳng vuông góc