SBT Toán 8 (Cánh diều) Bài 1: Định lí Pythagore

SBT Toán 8 (Cánh diều) Bài 1: Định lí Pythagore

Mai Hương Ngày: 26-01-2024 Lớp 8

209

Toptailieu.vn biên soạn và giới thiệu lời giải SBT Toán 8 (Cánh diều) Bài 1: Định lí Pythagore hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi vở bài tập Toán 8 Bài 1 từ đó học tốt môn Toán 8.

SBT Toán 8 (Cánh diều) Bài 1: Định lí Pythagore

Bài 1 trang 87 SBT Toán 8 Tập 1: Tính độ dài $x, y, z$ ở các hình $3 a, 3 b, 3 c, 3 d$ (độ dài ở các hình là cùng đơn vị đo):

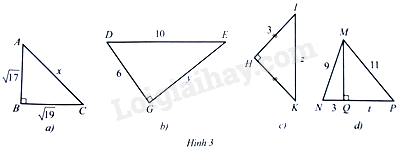
Sách bài tập Toán 8 Bài 1 (Cánh diều): Định lí Pythagore (ảnh 1)

Lời giải:

Áp dụng định lí Pythagore, ta có:

a) $A C^{2} = A B^{2} + B C^{2}$ , suy ra $x^{2} = {(\sqrt{17})}^{2} + {(\sqrt{19})}^{2} = 36$

Vậy $x = 6$

b) $D E^{2} = D G^{2} + G E^{2}$ , suy ra $10^{2} = 6^{2} + y^{2}$

Vậy $y = 8$

c) $I K^{2} = H I^{2} + H K^{2}$ , suy ra $z^{2} = 3^{2} + 3^{2}$

Vậy $z = \sqrt{18}$

d) Do tam giác $M N Q$ vuông tại $Q$ nên theo định lí Pythagore ta cóL

$M N^{2} = M Q^{2} + N Q^{2}$ . Suy ra $M Q^{2} = M N^{2} - N Q^{2}$ . Do đó, $M Q^{2} = 9^{2} - 3^{2} = 72$

Do tam giác $M N Q$ vuông tại $Q$ nên theo định lí Pythagore ta có:

$M P^{2} = M Q^{2} + P Q^{2}$ . Suy ra $P Q^{2} = M P^{2} - M Q^{2}$ . Do đó $t^{2} = 11^{2} - 72 = 49$

Vậy $t = \sqrt{49} = 7$ .

Bài 2 trang 88 SBT Toán 8 Tập 1: Hình 4 mô tả một chiếc thước của người thợ sử dụng khi xây móng nhà để kiểm tra xem hai phần móng nhà có vuông góc với nhau hay không . Trên hình, ta đo được $A B = 4 d m$ , $A C = 3 d m$ và $B C = 5 d m$ . Em hãy giải thích vì sao hai cạnh của chiếc thước đó vuông góc với nhau.

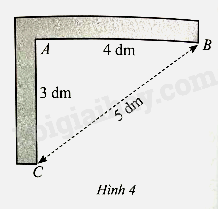
Sách bài tập Toán 8 Bài 1 (Cánh diều): Định lí Pythagore (ảnh 2)

Lời giải:

Ta có: $5^{2} = 25; 4^{2} + 3^{2} = 16 + 9 = 25$ nên $5^{2} = 4^{2} + 3^{2}$ . Do đó tam giác $A B C$ vuông tại $A$ (theo định lí Pythagore đảo). vậy hai cạnh của chiếc thước đó vuông góc với nhau.

Bài 3 trang 88 SBT Toán 8 Tập 1: Tính chu vi của tứ giác $A B C D$ ở Hình 5 (làm tròn kết quả đến hàng phần trăm của centimet). Biết rằng độ dài cạnh mỗi ô vuông là 1 cm.

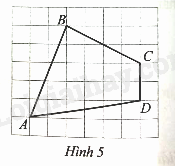
Sách bài tập Toán 8 Bài 1 (Cánh diều): Định lí Pythagore (ảnh 3)

Lời giải:

Ta vẽ thêm các điểm $M, N, P$ như hình vẽ:

Sách bài tập Toán 8 Bài 1 (Cánh diều): Định lí Pythagore (ảnh 4)

Ta có: $A M = 5 c m$ , $B M = 2 c m$ , $B N = 4 c m$ , $C N = 2 c m$ , $C D = 2 c m$ , $D P = 1 c m$ , $A P = 6 c m$

$A B^{2} = A M^{2} + B M^{2} = 29$ suy ra $A B = \sqrt{29} c m$

$B C^{2} = B N^{2} + C N^{2} = 20$ suy ra $B C = \sqrt{20} c m$

$D A^{2} = D P^{2} + A P^{2} = 37$ suy ra $D A = \sqrt{37} c m$ .

Chu vi của tứ giác $A B C D$ là: $\sqrt{29} + \sqrt{20} + 2 + \sqrt{37} \approx 17, 94 (c m)$ .

Bài 4 trang 88 SBT Toán 8 Tập 1: Cho tam giác $A B C$ vuông cân tại $A$ có độ dài cạnh góc vuông $A B$ và $A C$ là 4 cm. Kẻ đường cao $A D$ của tam giác $A B C$ .

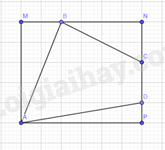
a) Tính độ dài cạnh đáy $B C$ (làm tròn kết quả đến hàng phần trăm của centimet)

b) Tính độ dài đường cao $A D$ (làm tròn kết quả đến hàng phần trăm của centimet)

Lời giải:

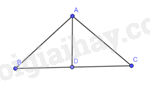
Sách bài tập Toán 8 Bài 1 (Cánh diều): Định lí Pythagore (ảnh 5)

a) Áp dụng định lí Pythagore ta có:

$B C^{2} = A B^{2} + A C^{2} = 32$

Suy ra $B C = \sqrt{32} \approx 5, 66 (c m)$

b) Lại có $Δ A B D = Δ A C D$ (cạnh huyền-cạnh góc vuông)

Suy ra $B D = C D$ . Vậy $D$ là trung điểm của $B C$ .

Do đó $C D = \frac{B C}{2} = \frac{\sqrt{32}}{2} \approx 2, 83 (c m)$

Tam giác $A C D$ vuông tại $D$ nên ta tính được $A D \approx 2, 83 (c m)$ .

Bài 5 trang 88 SBT Toán 8 Tập 1: Cho tam giác $A B C$ vuông cân tại $A$ . Qua $A$ kẻ đường thẳng $d$ bất kì sao cho đường thẳng $d$ không cắt đoạn thẳng $B C$ . Gọi $D, E$ lần lượt là hình chiếu của $B, C$ trên đường thẳng $d$ . Chứng minh $A D^{2} + A E^{2}$ không phụ thuộc vào vị trí của đường thẳng $d$ .

Lời giải:

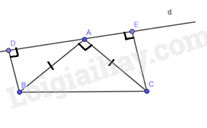
Sách bài tập Toán 8 Bài 1 (Cánh diều): Định lí Pythagore (ảnh 6)

Ta chứng minh được:

$\hat{B A D} + \hat{A B D} = 90^{\circ}$ và $\hat{B A D} + \hat{C A E} = 90^{\circ}$ nên $\hat{A B D} = \hat{C A E}$ .

$Δ A B D = Δ C A E$ (cạnh huyền – góc nhọn)

Suy ra $A D = C E$

Do đó $A D^{2} + A E^{2} = C E^{2} + A E^{2} = A C^{2}$ (vì tam giác $C A E$ vuông tại $E$ )

Vậy $A D^{2} + A E^{2}$ không phụ thuộc vào vị trí của đường thẳng $d$ .

Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:

Bài tập cuối chương 4

Bài 2: Tứ giác

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Từ khóa :

Giải bài tập Toán 7

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

295

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

315

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

343

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

290

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.