SBT Toán 8 (Cánh diều) Bài 4: Hình bình hành

Mai Hương Ngày: 26-01-2024 Lớp 8

233

Toptailieu.vn biên soạn và giới thiệu lời giải SBT Toán 8 (Cánh diều) Bài 4: Hình bình hành hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi vở bài tập Toán 8 Bài 4 từ đó học tốt môn Toán 8.

SBT Toán 8 (Cánh diều) Bài 4: Hình bình hành

Bài 16 trang 94 SBT Toán 8 Tập 1: Cho tam giác $A B C$ có $A B = A C = 3 c m$ . Từ điểm $M$ thuộc cạnh $B C$ , kẻ $M D$ song song với $A C$ và $M E$ song song với $A B$ (điểm $D, E$ lần lượt thuộc cạnh $A B, A C$ ). Tính chu vi của tứ giác $A D M E$ .

Lời giải:

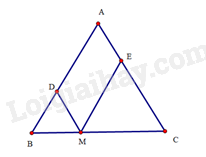
Sách bài tập Toán 8 Bài 4 (Cánh diều): Hình bình hành (ảnh 1)

Do $A B = A C$ nên tam giác $A B C$ cân tại $A$ . Suy ra $\hat{A B C} = \hat{A C B}$ .

Mà $\hat{A B C} = \hat{E M C}$ (hai góc đồng vị), suy ra $\hat{A C B} = \hat{E M C}$ .

Do đó, tam giác $E C M$ cân tại $E$ . Suy ra $M E = C E$ .

Tứ giác $A D M E$ có $M D / / A E, M E / / A D$ nên $A D M E$ là hình bình hành. Vậy chu vi của hình bình hành $A D M E$ là:

$2 (A E + M E) = 2 (A E + C E) = 2 A C = 6 c m$

Bài 17 trang 94 SBT Toán 8 Tập 1: Cho tam giác $A B C$ có các đường trung tuyến $B D$ và $C E$ . Lấy các điểm $H, K$ sao cho $E$ là trung điểm của $C H, D$ là trung điểm của $B K$ . Chứng minh:

a) Các tứ giác $A H B C, A K C B$ là hình bình hành;

b) $A$ là trung điểm của $H K$ .

Lời giải:

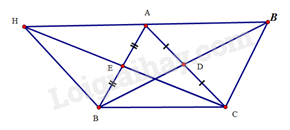
Sách bài tập Toán 8 Bài 4 (Cánh diều): Hình bình hành (ảnh 2)

a) Tứ giác $A H B C$ có $E$ là trung điểm của hai đường chéo $A B$ và $C H$ nên $A H B C$ là hình bình hành.

Tương tự, ta chứng minh được tứ giác $A K C B$ là hình bình hành.

b) Do $A H B C$ là hình bình hành nên $A H / / B C$ , $A H = B C$ . Tương tự, $A K C B$ là hình bình hành nên $A K / / B C, A K = B C$ . Suy ra ba điểm $H, A, K$ thẳng hàng và $A H = A K$ . Vậy $A$ là trung điểm của $H K$ .

Bài 18 trang 95 SBT Toán 8 Tập 1: Cho hình bình hành $A B C D$ . Trên cạnh $A D, B C$ lần lượt lấy điểm $E, F$ sao cho $A E = C F$ . Trên cạnh $A B, C D$ lần lượt lấy điểm $M, N$ sao cho $B M, D N$ . Chứng minh:

a) Tứ giác $E M F N$ là hình bình hành;

b) Bốn đường thẳng $A C, B D, E F, M N$ cùng đi qua một điểm.

Lời giải:

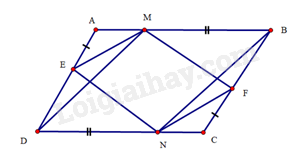
Sách bài tập Toán 8 Bài 4 (Cánh diều): Hình bình hành (ảnh 3)

a) Do $A B C D$ là hình bình hành nên $A D = B C$ và $A B = C D$ ; $\hat{A} = \hat{C}$ và $\hat{A B C} = \hat{C D A}$ .

Mà $A E = C F$ và $B M = D N$ , suy ra $D E = B F$ và $A M = C N$ .

$Δ A E M = Δ C F N$ (c.g.c). Suy ra $E M = F N$

$Δ B F M = Δ D E N$ (c.g.c). Suy ra $F M = E N$

Tứ giác EFMN có $E M = F N$ và $F M = E N$ nên $E M F N$ là hình bình hành.

b) Tứ giác $B M D N$ có $B M = D N$ và $B M / / D N$ nên $B M D N$ là hình bình hành.

Do $A B C D, E M F N, B M D N$ đều là hình bình hành nên các đường chéo của mỗi hình bình hành cắt nhau tại trung điểm của mỗi đường.

Vậy $A C, B D, E F, M N$ cùng đi qua trung điểm của mỗi đường.

Bài 19 trang 95 SBT Toán 8 Tập 1: Cho tam giác nhọn $A B C$ có ba đường cao $A M, B N, C P$ cắt nhau tại $H$ . Qua $B$ kẻ tia $B x$ vuông góc với $A B$ . Qua $C$ kẻ tia $C y$ vuông góc với $A C$ . Gọi $D$ là giao điểm của $B x$ và $C y$ (Hình 15)

a) Chứng minh tứ giác $B D C H$ là hình bình hành;

b) Tam giác $A B C$ có điều kiện gì thi ba điểm $A, D, H$ thẳng hàng?

c) Tìm mối liên hệ giữa góc $A$ và góc $D$ của tứ giác $A B C D$ .

d) Giả sử $H$ là trung điểm của $A M$ . Chứng minh diện tích của tam giác $A B C$ bằng diện tích của tứ giác $B H C D$ .

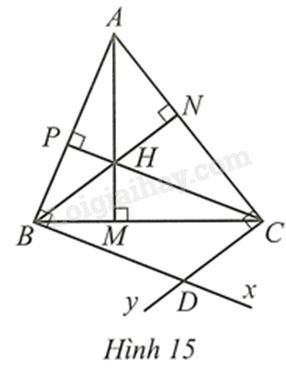
Sách bài tập Toán 8 Bài 4 (Cánh diều): Hình bình hành (ảnh 4)

Lời giải:

a) Ta có: $\hat{A P C} = \hat{A B D} = 90^{\circ}$ và $\hat{A P C}, \hat{A B D}$ nằm ở vị trí đồng vị nên $C P / / B D$ .

Tương tự ta chứng minh được $B N / / C D$ .

Tứ giác $B D C H$ có $B D / / C H, B H / / C D$ nên $B D C H$ là hình bình hành.

b) Để ba điểm $A, D, H$ thẳng hàng thì $M$ phải thuộc $D H$ . Mà $M$ thuộc $B C$ , suy ra $M$ là giao điểm của $B C$ và $D H$ .

Do $B D C H$ là hình bình hành nên hai đường chéo $B C$ và $D H$ cắt nhau tại trung điểm của mỗi đường. suy ra $M$ là trung điểm $B C$ .

Khi đó $Δ A B M = Δ A C M$ (c.g.c). Suy ra $A B = A C$ .

Dễ thấy nếu tam giác $A B C$ có $A B = A C$ thì ba điểm $A, D, H$ thẳng hàng.

Vậy tam giác $A B C$ cân tại $A$ thì $A, D, H$ thẳng hàng.

c) Xét tứ giác $A B C D$ , ta có: $\hat{B A C} + \hat{D B A} + \hat{C D B} + \hat{A C D} = 360^{\circ}$ .

Mà $\hat{D B A} = \hat{A C D} = 90^{\circ}$ , suy ra tính được $\hat{B A C} + \hat{C D B} = 3180^{\circ}$

Vậy góc $A$ và góc $D$ của tứ giác $A B C D$ là hai góc bù nhau.

d) Do $H$ là trung điểm của $A M$ nên $H M = \frac{1}{2} A M$

Ta có diện tích tam giác $A B C$ bằng: $\frac{1}{2} . A M . B C = H M . B C$ .

Ta chứng minh được $Δ B C H = Δ C B D$ (c.c.c.). Suy ra diện tích tứ giác $B H C D$ bằng 2 lần diện tích tam giác $B C H$ .

Do đó, diện tích tứ giác $B H C D$ bằng: $(\frac{1}{2} . H M . B C = H M . B C)$ vạy diện tích tam giác $A B C$ bằng điệnt tích của tứ giác $B H C D$ .

Bài 20 trang 95 SBT Toán 8 Tập 1: Cho hình bình hành $A B C D$ có $\hat{A} > 90^{\circ}$ , $A B > B C$ . Trên đường thẳng vuông góc với $B C$ tại $C$ lấy hai điểm $E, F$ sao cho $C E, C F, B C$ . Trên đường thẳng vuông góc với $C D$ tại $C$ lấy hai điểm $P, Q$ sao cho $C P = C Q = C D$ (Hình 16). Chứng minh:

a) Tứ giác $E P F F G$ là hình bình hành;

b) $A C ⊥ E P$ .

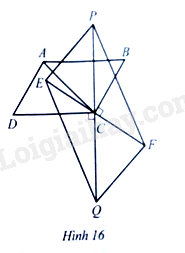
Sách bài tập Toán 8 Bài 4 (Cánh diều): Hình bình hành (ảnh 5)

Lời giải:

a) Tứ giác $E P F Q$ có hai đường chéo $E F$ và PQ cắt nhau tại trung điểm $C$ của mỗi đường nên $E F P Q$ là hình binh hành.

b) Gọi $H$ là giao điểm của $A C$ và $E P$ , $K$ là giao điểm của $A B$ và $P Q$ .

Do $A B C D$ là hình bình hành nên $A B / / C D, A D = B C$ , $\hat{B} = \hat{D}$ .

Vì $A B / / C D$ nên $\hat{B K C} = \hat{D C K} = 90^{\circ}$ (hai góc so le trong). Suy ra tam giác $B C K$ vuông tại $K$ . Do đó,

$\hat{B} = \hat{B C K} = 90^{\circ}$

Mặt khác, ta có $\hat{E C P} + \hat{B C K} = \hat{B C E} = 90^{\circ}$ nên $\hat{D} = \hat{E C P}$ .

Xét hai tam giác $A C D$ và $E P C$ , ta có:

$A D = E C$ (vì cùng bằng $B C$ ); $\hat{D} = \hat{E C P}; C D = P C$

Suy ra $Δ A C D = Δ E P C$ (c.g.c). Do đó $\hat{A C D} = \hat{E P C}$ (hai góc tương ứng) hay $\hat{A C D} = \hat{H P C}$ . Mà $\hat{A C D} + \hat{P C H} = \hat{D C P} = 90^{\circ}$ , suy ra $\hat{H P C} + \hat{P C H} = 90^{\circ}$