Cho tam giác nhọn ABC có ba đường cao AM, BN, CP cắt nhau tại H. Qua B kẻ tia Bx vuông góc với AB

Mai Hương Ngày: 23-01-2024 Lớp 8

199

Với giải Bài 19 trang 95 SBT Toán 8 Tập 1 Cánh diều chi tiết trong Bài 4: Hình bình hành giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:

Cho tam giác nhọn ABC có ba đường cao AM, BN, CP cắt nhau tại H. Qua B kẻ tia Bx vuông góc với AB

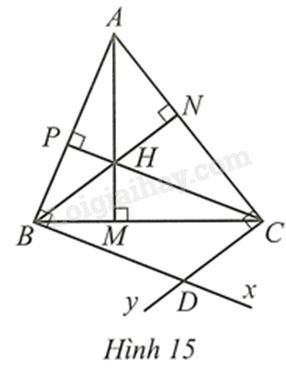
Bài 19 trang 95 SBT Toán 8 Tập 1: Cho tam giác nhọn $A B C$ có ba đường cao $A M, B N, C P$ cắt nhau tại $H$ . Qua $B$ kẻ tia $B x$ vuông góc với $A B$ . Qua $C$ kẻ tia $C y$ vuông góc với $A C$ . Gọi $D$ là giao điểm của $B x$ và $C y$ (Hình 15)

a) Chứng minh tứ giác $B D C H$ là hình bình hành;

b) Tam giác $A B C$ có điều kiện gì thi ba điểm $A, D, H$ thẳng hàng?

c) Tìm mối liên hệ giữa góc $A$ và góc $D$ của tứ giác $A B C D$ .

d) Giả sử $H$ là trung điểm của $A M$ . Chứng minh diện tích của tam giác $A B C$ bằng diện tích của tứ giác $B H C D$ .

Sách bài tập Toán 8 Bài 4 (Cánh diều): Hình bình hành (ảnh 4)

Lời giải:

a) Ta có: $\hat{A P C} = \hat{A B D} = 90^{\circ}$ và $\hat{A P C}, \hat{A B D}$ nằm ở vị trí đồng vị nên $C P / / B D$ .

Tương tự ta chứng minh được $B N / / C D$ .

Tứ giác $B D C H$ có $B D / / C H, B H / / C D$ nên $B D C H$ là hình bình hành.

b) Để ba điểm $A, D, H$ thẳng hàng thì $M$ phải thuộc $D H$ . Mà $M$ thuộc $B C$ , suy ra $M$ là giao điểm của $B C$ và $D H$ .

Do $B D C H$ là hình bình hành nên hai đường chéo $B C$ và $D H$ cắt nhau tại trung điểm của mỗi đường. suy ra $M$ là trung điểm $B C$ .

Khi đó $Δ A B M = Δ A C M$ (c.g.c). Suy ra $A B = A C$ .

Dễ thấy nếu tam giác $A B C$ có $A B = A C$ thì ba điểm $A, D, H$ thẳng hàng.

Vậy tam giác $A B C$ cân tại $A$ thì $A, D, H$ thẳng hàng.

c) Xét tứ giác $A B C D$ , ta có: $\hat{B A C} + \hat{D B A} + \hat{C D B} + \hat{A C D} = 360^{\circ}$ .

Mà $\hat{D B A} = \hat{A C D} = 90^{\circ}$ , suy ra tính được $\hat{B A C} + \hat{C D B} = 3180^{\circ}$

Vậy góc $A$ và góc $D$ của tứ giác $A B C D$ là hai góc bù nhau.

d) Do $H$ là trung điểm của $A M$ nên $H M = \frac{1}{2} A M$

Ta có diện tích tam giác $A B C$ bằng: $\frac{1}{2} . A M . B C = H M . B C$ .

Ta chứng minh được $Δ B C H = Δ C B D$ (c.c.c.). Suy ra diện tích tứ giác $B H C D$ bằng 2 lần diện tích tam giác $B C H$ .

Do đó, diện tích tứ giác $B H C D$ bằng: $(\frac{1}{2} . H M . B C = H M . B C)$ vạy diện tích tam giác $A B C$ bằng điệnt tích của tứ giác $B H C D$ .