SBT Toán 8 (Cánh diều) Bài 7: Hình vuông

Mai Hương Ngày: 26-01-2024 Lớp 8

209

Toptailieu.vn biên soạn và giới thiệu lời giải SBT Toán 8 (Cánh diều) Bài 7: Hình vuông hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi vở bài tập Toán 8 Bài 7 từ đó học tốt môn Toán 8.

SBT Toán 8 (Cánh diều) Bài 7: Hình vuông

Bài 31 trang 102 SBT Toán 8 Tập 1: Cho hình vuông $A B C D$ có hai đường chéo $A C$ và $B D$ cắt nhau tại $O$ . Trên tia đối của tia $C B$ lấy điểm $K$ sao cho $B C = C K$ . Từ điểm $B$ kẻ đường thẳng song song với $A C$ cắt tia $D C$ tại $E$ . Gọi $F$ là trung điểm của $B E$ .

a) Chứng minh các tứ giác $B O C F$ và $B D K E$ đều là hình vuông.

b) Tứ giác $C D O F$ có thể là hình vuông không? Vì sao?

Lời giải:

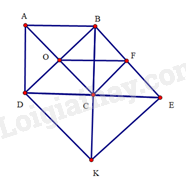
Sách bài tập Toán 8 Bài 7 (Cánh diều): Hình vuông (ảnh 1)

a) Tứ giác $A B C D$ là hình vuông suy ra $\hat{A C B} = 45^{\circ}, O B = O C, \hat{B O C} = \hat{D O C} = 90^{\circ}$ .

Ta có: $\hat{B O F} = \hat{D O C}$ (hai góc đồng vị) nên $\hat{O B F} = 90^{\circ}; \hat{C B E} = \hat{A C B}$ (hai góc so le trong) nên $\hat{C B E} = 45^{\circ}$ .

Từ đó ta chứng minh được tam giác $B D E$ vuông cân tại $B$ và tam giác $B C E$ vuông cân tại $C$ . Suy ra $B D = B E$ và $B C = E C$ .

$Δ B C F = Δ E C F$ (c.c.c). Suy ra ta tính được $\hat{B F C} = \hat{E F C} = 90^{\circ}$

Tứ giác $B O C F$ có $\hat{B O C} = \hat{O B F} = \hat{B F C} = 90^{\circ}$ nên $B O C F$ là hình chữ nhật.

Hình chữ nhật $B O C F$ có $O B = O C$ nên $B O C F$ là hình vuông.

Ta có: $B C = C D$ và $B C = C E$ nên $C D = C E$ .

Tứ giác $B D K E$ có hai đường chéo $B K$ và $D E$ cắt nhau tại trung điểm $C$ của mỗi đường nên $B D K E$ là hình bình hành.

Hình bình hành $B D K E$ có $\hat{D B E} = 90^{\circ}$ nên $B D K E$ là hình chữ nhật

Hình chữ nhật $B D K E$ có $B D = B E$ nên $B D K E$ là hình vuông

b) Tứ giác $C D O F$ có $\hat{O D C} = 45^{\circ}$ nên $C D O F$ không thể là hình vuông.

Bài 32 trang 102 SBT Toán 8 Tập 1: Cho hình chữ nhật $A B C D$ có hai cạnh kề không bằng nhau. Tia phân giác của các góc $A$ và $B$ cắt nhau tại $E$ . Tia phân giác của các góc $C$ và $D$ cắt nhau tại $F$ . Gọi $G$ là giao điểm của $A E$ và $D F$ , $H$ là giao điểm của $B E$ và $C F$ . Chứng minh:

a) $G H / / C D$

b) Tứ giác $G F H E$ là hình vuông

Lời giải:

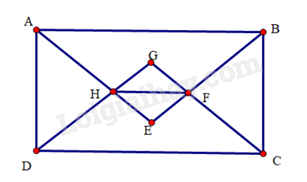
Sách bài tập Toán 8 Bài 7 (Cánh diều): Hình vuông (ảnh 2)

a) Do $A B C D$ là hình chữ nhật nên $\hat{D A B} = \hat{A B C} = \hat{B C D} = \hat{C D A} = 90^{\circ}$

Mà $A E, B E, C F, D F$ lần lượt là các tia phân giác của các góc $D A B, A B C, B C D, C D A$

suy ra $\hat{D A E} = \hat{E A B} = \hat{A B E} = \hat{E B C} = \hat{B C F} = \hat{F C D} = \hat{C D F} = \hat{F D A} = 45^{\circ}$

Do đó, các tam giác $E A B, F C D, G A D, H B C$ đều là tam giác vuông cân.

$Δ G A D = Δ H B C$ (g.c.g). Suy ra $G D = H C$ . Mà $F D = F C$ , suy ra $F G = F H$ .

Do đó, tam giác $F G H$ vuông cân tại $F$ . Suy ra $\hat{F G H} = 45^{\circ}$ .

Ta có: $\hat{F G H} = \hat{C D F} = 45^{\circ}$ và $\hat{F G H}, \hat{C D F}$ nằm ở vị trí đồng vị nên $G H / / C D$ .

b) $\hat{E G F} = \hat{A G D} = 90^{\circ}$ (hai góc đối đỉnh)

Tứ giác $G F H E$ là hình chữ nhật.

Hình chữ nhật $G F H E$ có $F G = F H$ nên $G F H E$ là hình vuông.

Bài 33 trang 102 SBT Toán 8 Tập 1: Cho hình bình hành $A B C D$ . Ở phía ngoài hình bình hành, vẽ các hình vuông $A B E F$ và $A D G H$ (Hình 26). Chứng minh:

a) $Δ A H F = Δ A D C$

b) $A C ⊥ H F$ .

Sách bài tập Toán 8 Bài 7 (Cánh diều): Hình vuông (ảnh 3)

Lời giải:

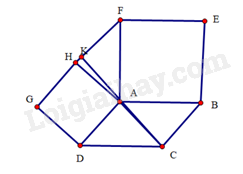
Sách bài tập Toán 8 Bài 7 (Cánh diều): Hình vuông (ảnh 4)

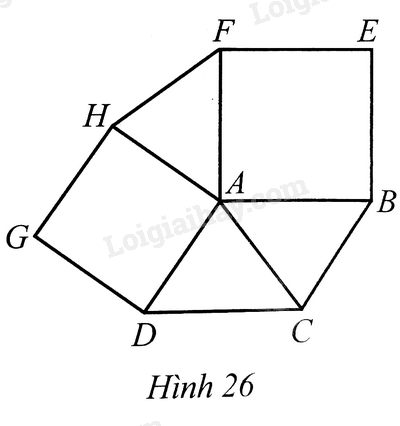
Gọi $K$ là giao điểm của $A C$ và $H F$

a) Do $A B E F$ và $A D G H$ đều là hình vuông nên $\hat{B A F} = \hat{D A H} = 90^{\circ}, A H = B A, A H = D A$

Do $A B C D$ là hình bình hành nên $B A = D C$ . Suy ra $A F = D C$

Ta chứng minh được $\hat{H A F} + \hat{D A B} = 180^{\circ}$ và $\hat{A D C} + \hat{D A B} = 180^{\circ}$

Suy ra $\hat{H A F} = \hat{A D C}$

Xét hai tam giác $H A F$ và $A D C$ , ta có: $A H = D A, \hat{H A F} = \hat{A D C}, A F = D A$

Suy ra $Δ H A F = Δ A D C$ (c.g.c)

b) Ta có: $\hat{H A K} + \hat{D A H} + \hat{D A C} = \hat{C A K} = 180^{\circ}$ và $\hat{D A H} = 90^{\circ}$ nên $\hat{H A K} + \hat{D A C} = 90^{\circ}$

Mà $\hat{A H F} = \hat{D A C}$ (vì $Δ H A F = Δ A D C$ ), suy ra $\hat{H A K} + \hat{A H F} = 90^{\circ}$

Trong tam giác $A H K$ , ta có: $\hat{A K H} + \hat{H A K} + \hat{A H F} = 180^{\circ}$ . Suy ra $\hat{A K H} = 90^{\circ}$

Vậy $A K ⊥ H K$ hai $A C ⊥ H F$ .

Bài 34 trang 102 SBT Toán 8 Tập 1: Cho tam giác $A B C$ có các đường trung tuyến $B D, C E$ cắt nhau tại $G$ . Gọi $F, H$ lần lượt là trung điểm của $B G, C G$ .

a) Tứ giác $E F H D$ là hình gì? Vì sao?

b) Tìm điều kiện của tam giác $A B C$ để tứ giác $E F H D$ là hình vuông.

Lời giải:

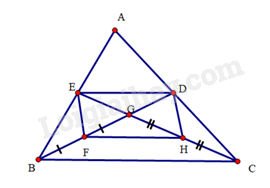
Sách bài tập Toán 8 Bài 7 (Cánh diều): Hình vuông (ảnh 5)

a) Do $G$ là trọng tâm tam giác $A B C$ nên $D G = \frac{1}{2} B G, E G = \frac{1}{2} C G$ . Mà $F, H$ lần lượt là trung điểm của $B G, C G$ nên $D G = B F = F G, E G = C H = H G$ .

Tứ giác $E F H G$ có hai đường chéo $E H$ và $D F$ cắt nhau tại trung điểm của mỗi đường nên $E F H G$ là hình bình hành.

b) Để hình bình hành $E F H G$ là hình vuông thì $E H = D F$ và $E H ⊥ D F$

suy ra $B G = C G, E G = D G$ và $B D ⊥ C E$ .

$Δ B E G = Δ C D G$ (c.g.c). Suy ra $B E = C D$ . Mà $A B = 2 B E, A C = 2 C D$ , suy ra $A B = A C$ .

Dễ thấy nếu $A B = A C$ và $B D ⊥ C E$ thì tứ giác $E F H G$ là hình vuông.

Vậy tam giác $A B C$ cân tại $A$ có đường trung tuyến $B D$ , $C E$ vuông góc với nhau thì tứ giác $E F H G$ là hình vuông.

Bài 35 trang 103 SBT Toán 8 Tập 1: Cho hình vuông $A B C D$ có $A B = 12 c m$ . Trên cạnh $C D$ lấy điểm $E$ sao cho $D E = 5 c m$ . Tia phân giác của góc $B A E$ cắt $B C$ tại $F$ . Trên tia đối của tia $B C$ lấy điểm $M$ sao cho $B M = D E$ .

a) Chứng minh $A E = A M = D E$

b) Tính độ dài $B F$ .

Lời giải:

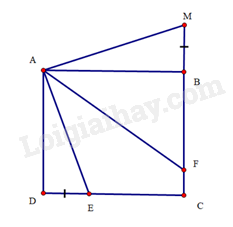
Sách bài tập Toán 8 Bài 7 (Cánh diều): Hình vuông (ảnh 6)

a) $Δ A D E = Δ A B M$ (c.g.c)

Suy ra $A E = A M$ và $\hat{D A E} = \hat{B A M}$ .

Do $A F$ là tia phân giác của $\hat{B A E}$ nên $\hat{E A F} = \hat{B A F}$ .

Suy ra $\hat{D A E} + \hat{E A F} = \hat{B A M} + \hat{B A F}$ hay $\hat{D A F} = \hat{M A F}$ .

Mà $\hat{D A F} = \hat{M F A}$ (hai góc so le trong) , suy ra $\hat{M F A} = \hat{M A F}$

Do đó, tam giác $M A F$ cân tại $M$ . Suy ra $A M = F M$

Mà $A E = A M$ , suy ra $A E = A M = F M$ .

b) Trong tam giác $A D E$ vuông tại $D$ , ta có: $A E^{2} = A D^{2} + D E^{2}$

Suy ra $A E = 13 c m$ . Mà $F M = A E$ , suy ra $F M = 13 c m$ .

Ta có: $F M = B M + B F$ . Mà $B M = D E = 5 c m$ và $F M = 13 c m$ , suy ra $B F = 8 c m$ .

Bài 36 trang 103 SBT Toán 8 Tập 1: Cho hình vuông $A B C D$ . Lấy điểm $E$ thuộc cạnh $C D$ và điểm $F$ thuộc tia đối của tia $B C$ sao cho $B F = D E$ .

a) Chứng minh tam giác $A E F$ là tam giác vuông cân

b) Gọi $I$ là trung điểm của $E F$ . Trên tia đối của tia $I A$ lấy điểm $K$ sao cho $I K = I A$ . Chứng minh tứ giác $A E K F$ là hình vuông.

c) Chứng minh $I$ thuộc đường thẳng $B D$ .

Lời giải:

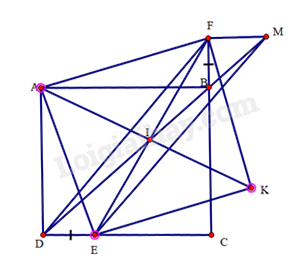
Sách bài tập Toán 8 Bài 7 (Cánh diều): Hình vuông (ảnh 7)

Từ điểm $F$ kẻ đường thẳng song song với $C D$ cắt đường thẳng $B D$ tại $M$

a) $Δ A D E = Δ A B F$ (c.g.c)

Suy ra $A E = A F$ và $\hat{D A E} = \hat{B A F}$

Suy ra $\hat{D A E} + \hat{B A E} = \hat{B A F} + \hat{B A E}$ hay $\hat{B A D} = \hat{E A F}$ .

Do đó, $\hat{E A F} = 90^{\circ}$

Tam giác $A E F$ có $\hat{E A F} = 90^{\circ}, A E = A F$ nên tam giac $A E F$ vuông cân tại $A$ .

b) Tứ giác $A E K F$ có hai đường chéo $A K, E F$ cắt nhau tại trung điểm $I$ của mỗi đường nên $A E K F$ là hình bình hành

hình bình hành $A E K F$ có $\hat{E A F} = 90^{\circ}$ nên $A E K F$ là hình chữ nhật.

hình chữ nhật $A E K F$ có $A E = A F$ nên $A E K F$ là hình vuông.

c) Do $A B C D$ là hình vuông nên ta tính được $\hat{C B D} = 45^{\circ}$ . Mà $\hat{F B M} = \hat{C B D}$ (hai góc đối đỉnh), suy ra $\hat{F B M} = 45^{\circ}$ .