SBT Toán 8 (Cánh diều) Bài 6: Hình thoi

Mai Hương Ngày: 26-01-2024 Lớp 8

180

Toptailieu.vn biên soạn và giới thiệu lời giải SBT Toán 8 (Cánh diều) Bài 6: Hình thoi hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi vở bài tập Toán 8 Bài 6 từ đó học tốt môn Toán 8.

SBT Toán 8 (Cánh diều) Bài 6: Hình thoi

Bài 26 trang 99 SBT Toán 8 Tập 1: Cho hình thoi $A B C D$ có góc $B$ tù. Kẻ $B E$ vuông góc $A D$ tại $E$ , $B F$ vuông góc với $C D$ tại $F$ . Gọi $M, N$ lần lượt là giao điểm của $B E, B F$ với $A C$ . Chứng minh tứ giác $B M D N$ là hình thoi.

Lời giải:

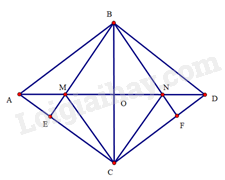
Sách bài tập Toán 8 Bài 6 (Cánh diều): Hình thoi (ảnh 1)

Gọi $O$ là giao điểm của $A C$ và $B D$

Do $A B C D$ là hình thoi nên $A C$ vuông góc với $B D$ tại trung điểm $O$ của $B D$ . Suy ra $A C$ là đường trung trực của $B D$ . Do đó $B M = D M, B N = D N$ .

Do $A B C D$ là hình thoi nên $B A = B C, \hat{B A E} = \hat{B C F}$ .

Suy ra $Δ A B E = Δ B C F$ (cạnh huyền – góc nhọn kề)

Do đó $\hat{A B E} = \hat{C B F}$ . Mà $\hat{A B D} = \hat{C B D}$ , suy ra $\hat{M B O} = \hat{N B O}$ .

$Δ M B O = Δ N B O$ (cạnh góc vuông – góc nhọn). suy ra $B M = B N$

Mà $B M = D M$ và $B N = D N$ , suy ra $B M = D M = B N = D N$ .

Tứ giác $B M D N$ có $B M = D M = B N = D N$ nên $B M D N$ là hình thoi.

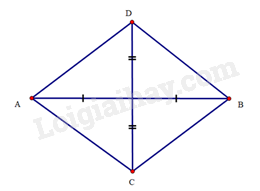
Bài 27 trang 99 SBT Toán 8 Tập 1: Cho một hình thoi có độ dài hai đường chéo là $\frac{18}{5}$ m và $\frac{27}{10}$ m. Tính chu vi và diện tích của hình thoi đó.

Lời giải:

Sách bài tập Toán 8 Bài 6 (Cánh diều): Hình thoi (ảnh 2)

Xét hình thoi $A B C D$ có $A C = \frac{18}{5} m$ , $B D = \frac{27}{10} m$ .

Gọi $O$ là giao điểm của hai đường chéo $A C$ và $B D$ .

Do $A B C D$ là hình thoi nên $A C ⊥ B D, O$ là trung điểm của $A C$ và $B D$ .

Ta tính được:

$O A = \frac{A C}{2} = \frac{9}{5} m$

$O B = \frac{B D}{2} = \frac{27}{20} m$ .

Trong tam giác $O A B$ vuông tại $O$ , ta có: $A B^{2} = O A^{2} + O B^{2}$ . Suy ra $A B = \frac{9}{4} m$

Chu vi của hình thoi $A B C D$ là: $4. \frac{9}{4} = 9 (m)$

Diện tích của hình thoi $A B C D$ là: $\frac{1}{2} . \frac{18}{5} . \frac{27}{10} = \frac{243}{50} (m^{2})$ .

Bài 28 trang 100 SBT Toán 8 Tập 1: Cho tam giác $A B C$ nhọn có các đường cao $B D, C E$ . Tia phân giác của các góc $A C E, A B D$ cắt nhau tại $O$ và cắt $A B, A C$ lần lượt tại $M, N$ . Tia $B N$ cắt $C E$ tại $K$ , tia $C M$ cắt $B D$ tại $H$ . Chứng minh:

a) $B N ⊥ C M$

b) Tứ giác $M N H K$ là hình thoi.

Lời giải:

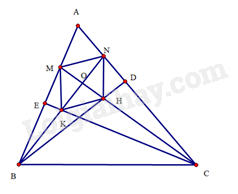
Sách bài tập Toán 8 Bài 6 (Cánh diều): Hình thoi (ảnh 3)

a) Do tam giác $A B D$ vuông tại $D$ và tam giác $A C E$ vuông tại $E$ nên $\hat{A B D} + \hat{A} = \hat{A C E} + \hat{A} = 90^{\circ}$ . Suy ra $\hat{A B D} = \hat{A C E}$ .

Mà $B N$ và $C M$ lần lượt là tia phân giác của $\hat{A B D}$ và $\hat{A C E}$ , suy ra $\hat{A B N} = \hat{D B N} = \hat{A C M} = \hat{E C M}$ .

Do tam giác $C E M$ vuông tại $E$ nên $\hat{E C M} + \hat{E M C} = 90^{\circ}$

Suy ra $\hat{A B N} + \hat{E M C} = 90^{\circ}$ hay $\hat{M B O} + \hat{B M O} = 90^{\circ}$ .

Do đó ta tính được $\hat{B O M} = 90^{\circ}$ . Vậy $B N ⊥ C M$ .

b) $Δ B M O = Δ B H O$ (cạnh góc vuông – góc nhọn kề). Suy ra $O M = O H$

$Δ C N O = Δ C K O$ (cạnh góc vuông – góc nhọn kề). Suy ra $O N = O K$ .

Tứ giác $M N H K$ có hai đường chéo $M H$ và $N K$ cắt nhau tại trung điểm $O$ của mỗi đường nên $M N H K$ là hình bình hành.

Hình bình hành $M N H K$ có $M H ⊥ N K$ nên $M N H K$ là hình thoi.

Bài 29 trang 100 SBT Toán 8 Tập 1: Cho góc $x O y$ khác góc bẹt. Dùng thước hai lề (thước có hai cạnh song song). Đặt thước hai lề sao cho một cạnh của thước trùng với cạnh $O x$ của góc $x O y$ , vẽ đường thẳng $a$ theo cạnh kia của thước. đặt thước hai lề sao cho một cạnh của thước trùng với cạnh $O y$ của góc $x O y$ . Chứng minh tia $O M$ là tia phân giác của góc $x O y$ .

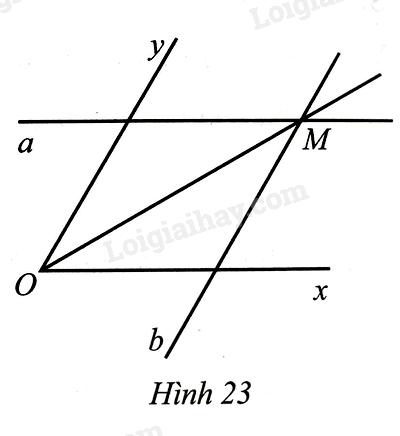
Sách bài tập Toán 8 Bài 6 (Cánh diều): Hình thoi (ảnh 4)

Lời giải:

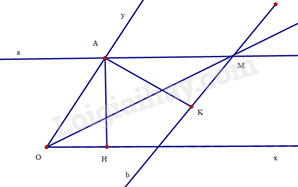
Sách bài tập Toán 8 Bài 6 (Cánh diều): Hình thoi (ảnh 5)

Gọi $A$ là giao điểm của đường thẳng $a$ với tia $O y$ , $B$ là giao điểm của đường thẳng $b$ với tia $O x$ . Kẻ $A H$ vuông góc với $O B$ tại $H, A K$ vuông góc với $B M$ tại $K$ . Do khoảng cách giữa hai lề của thước là không đổi nên ta có $A H = A K$ .

Tứ giác $O A M B$ có $A M / / O B, M B / / O A$ nên $O A M B$ là hình bình hành. Suy ra $\hat{A O H} = \hat{A M K}$ . Do đó $\hat{O A H} = \hat{M A K}$ .

$Δ A O H = Δ A M K$ (cạnh góc vuông – góc nhọn kề). Suy ra $O A = A M$ .

Hình bình hành $O A M B$ có $O A = A M$ nên $O A M B$ là hình thoi. Vậy $O M$ là tia phân giác của góc $x O y$ .

Bài 30 trang 100 SBT Toán 8 Tập 1: Cho hình thoi $A B C D$ có $A B = 2$ cm, $\hat{A} = \frac{1}{2} \hat{B}$ . Các điểm $H, K$ thay đổi lần lượt trên cạnh $A D, C D$ sao cho $\hat{H B K} = 60^{\circ}$ .

a) Chứng minh $D H + D K$ không đổi

b) Xác định vị trí của các điểm $H, K$ để độ dài $H K$ ngắn nhất. Tính độ dài ngắn nhất đó.

Lời giải:

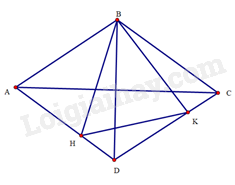
Sách bài tập Toán 8 Bài 6 (Cánh diều): Hình thoi (ảnh 6)

a) Do $A B C D$ là hình thoi nên $A B = D A = 2 c m, \hat{A B D} = \hat{C D B} = \frac{1}{2} \hat{A B C}$

Mà $\hat{B A D} = \frac{1}{2} \hat{A B C}$ , suy ra $\hat{B A D} = \hat{A B D}$ . Do đó tam giác $A B D$ cân tại $D$ . Suy ra $D A = D B$ .

Mà $A B = D A$ , suy ra $A B = D A = D B$ .

$Δ A B H = Δ D B K$ (g.c.g). Suy ra $A H = D K$ . Do đó $D H + D K = D H + A H = A D$ .

Vậy $D H + D K$ không đổi

b) Do $Δ A B H = Δ D B k$ nên $B H = B K$ .

Tam giác $B H K$ có $B H = B K$ và $\hat{H B K} = 60^{\circ}$ nên tam giác $B H K$ là tam giác đều.

Suy ra $H K = B H = B K$ .

Do đó, độ dài $H K$ ngắn nhất khi $B H$ và $B K$ ngắn nhất. Vậy $H, K$ lần lượt là hình chiếu của $B$ trên $A D, C D$ .

Khi đó $Δ A B H = Δ D B H$ (cạnh huyền – cạnh góc vuông)

Suy ra $A H = D H = \frac{A D}{2} = 1 c m$

Trong tam giác $A B H$ vuông tại $H$ , ta có: $A B^{2} = A H^{2} + B H^{2}$ . Suy ra ta tính được $B H = \sqrt{3} c m$ . Vậy độ dài ngắn nhất của $H K$ là $\sqrt{3}$ cm.