Với giải Bài 18 trang 95 SBT Toán 8 Tập 1 Cánh diều chi tiết trong Bài 4: Hình bình hành giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 8. Mời các bạn đón xem:
Cho hình bình hành ABCD. Trên cạnh AD, BC lần lượt lấy điểm E, F sao cho AE=CF
Bài 18 trang 95 SBT Toán 8 Tập 1: Cho hình bình hành . Trên cạnh lần lượt lấy điểm sao cho . Trên cạnh lần lượt lấy điểm sao cho . Chứng minh:
a) Tứ giác là hình bình hành;
b) Bốn đường thẳng cùng đi qua một điểm.
Lời giải:
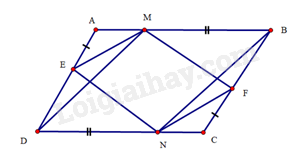
a) Do là hình bình hành nên và ; và .
Mà và , suy ra và .
(c.g.c). Suy ra
(c.g.c). Suy ra
Tứ giác EFMN có và nên là hình bình hành.
b) Tứ giác có và nên là hình bình hành.
Do đều là hình bình hành nên các đường chéo của mỗi hình bình hành cắt nhau tại trung điểm của mỗi đường.
Vậy cùng đi qua trung điểm của mỗi đường.
Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:
Bài 16 trang 94 SBT Toán 8 Tập 1: Cho tam giác có . Từ điểm thuộc cạnh , kẻ song song với
Bài 18 trang 95 SBT Toán 8 Tập 1: Cho hình bình hành . Trên cạnh lần lượt lấy điểm sao cho .
Bài 20 trang 95 SBT Toán 8 Tập 1: Cho hình bình hành có , . Trên đường thẳng vuông góc với tại
Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.