SBT Toán 8 (Cánh diều) Bài 2: Tứ giác

SBT Toán 8 (Cánh diều) Bài 2: Tứ giác

Mai Hương Ngày: 26-01-2024 Lớp 8

179

Toptailieu.vn biên soạn và giới thiệu lời giải SBT Toán 8 (Cánh diều) Bài 2: Tứ giác hay, chi tiết sẽ giúp học sinh dễ dàng trả lời câu hỏi vở bài tập Toán 8 Bài 2 từ đó học tốt môn Toán 8.

SBT Toán 8 (Cánh diều) Bài 2: Tứ giác

Bài 6 trang 89 SBT Toán 8 Tập 1: Tính các số đo $x, y, z$ ở các hình $6 a, 6 b, 6 c$ :

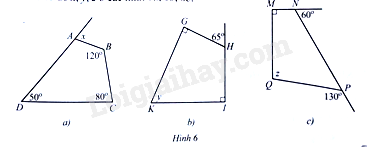
Sách bài tập Toán 8 Bài 2 (Cánh diều): Tứ giác (ảnh 1)

Lời giải:

a) Trong tứ giác $A B C D$ , ta có: $\hat{D A B} + \hat{B} + \hat{C} + \hat{D} = 360^{\circ}$ .

Do đó: $\hat{D A B} = 360^{\circ} - (\hat{B} + \hat{C} + \hat{D}) = 360^{\circ} - (120^{\circ} + 80^{\circ} + 50^{\circ}) = 110^{\circ}$

Ta có: $\hat{D A B} + x = 180^{\circ}$ (hai góc kề bù)

Suy ra $x = 180^{\circ} - 110^{\circ} = 70^{\circ}$

b) Ta có: $\hat{G H I} + 65^{\circ} = 180^{\circ}$ (hai góc kề bù). Suy ra $\hat{G H I} = 115^{\circ}$

Trong tứ giác $G H I K$ , ta có: $\hat{G} + \hat{G H I} + \hat{I} + \hat{K} = 360^{\circ}$

Do đó: $90^{\circ} + 115^{\circ} + 90^{\circ} + y = 360^{\circ}$ hay $y + 295^{\circ} = 360^{\circ}$ . Suy ra $y = 65^{\circ}$

c) Ta có: $\hat{M N P} + 60^{\circ} = 180^{\circ}$ (hai góc kề bù). Suy ra $\hat{M N P} = 120^{\circ}$

Ta lại có: $\hat{N P Q} + 130^{\circ} = 180^{\circ}$ (hai góc kề bù). Suy ra $\hat{N P Q} = 50^{\circ}$

Trong tứ giác $M N P Q$ , ta có: $\hat{M} + \hat{M N P} + \hat{N P Q} + \hat{Q} = 360^{\circ}$

Do đó $90^{\circ} + 120^{\circ} + 50^{\circ} + z = 360^{\circ}$ hay $z + 260^{\circ} = 360^{\circ}$ . Suy ra $z = 100^{\circ}$ .

Bài 7 trang 90 SBT Toán 8 Tập 1: Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác. Chứng minh tổng các góc ngoài của tứ giác $A B C D$ ở Hình 7 (tại mỗi đỉnh chỉ nhọn một góc ngoài):

$\hat{A_{1}} + \hat{B_{1}} + \hat{C_{1}} + \hat{D_{1}} = 360^{\circ}$ .

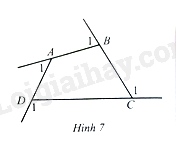
Sách bài tập Toán 8 Bài 2 (Cánh diều): Tứ giác (ảnh 2)

Lời giải:

Trong tứ giác $A B C D$ , ta có: $\hat{D A B} + \hat{A B C} + \hat{B C D} + \hat{C D A} = 360^{\circ}$

Ta có: $\hat{D A B} + \hat{A_{1}} = \hat{A B C} + \hat{B_{1}} = \hat{B C D} + \hat{C_{1}} = \hat{C D A} + \hat{D_{1}} = 180^{\circ}$ (các cặp góc kề bù)

Suy ra $(180^{\circ} - \hat{A_{1}}) + (180^{\circ} - \hat{B_{1}}) + (180^{\circ} - \hat{C_{1}}) + (180^{\circ} - \hat{D_{1}}) = 360^{\circ}$

Hay $720^{\circ} - (\hat{A_{1}} + \hat{B_{1}} + \hat{C_{1}} + \hat{D_{1}}) = 360^{\circ}$ . Vậy $\hat{A_{1}} + \hat{B_{1}} + \hat{C_{1}} + \hat{D_{1}} = 360^{\circ}$ .

Bài 8 trang 90 SBT Toán 8 Tập 1: a) Cho tứ giác $A B C D$ có $A B / / C D, \hat{B} = 135^{\circ}, \hat{D} = 70^{\circ}, \hat{A C B} = 25^{\circ}$ (Hình 8a). Tính số đo góc $D A C$ .

b) Cho tứ giác $G H I K$ có $\hat{K G H} = \hat{K} = 90^{\circ}, \hat{I} = 65^{\circ}$ . Trên $H I$ lấy điểm $E$ sao cho $\hat{E G H} = 25^{\circ}$ (Hình 8b). Tính số đo góc $G E I$ .

c) Cho tứ giác $M N P Q$ có $P M$ là tia phân giác của góc $N P Q, \hat{Q M N} = 110^{\circ}, \hat{N} = 120^{\circ}, \hat{Q} = 60^{\circ}$ (Hình 8c). Tính các số đo góc $N P M, M P Q, Q M P$ .

Lời giải:

a) Trong tam giác $A B C$ , ta có: $\hat{B A C} = 180^{\circ} - (\hat{B} + \hat{B C A}) = 20^{\circ}$

Do $A B / / C D$ nên $\hat{A C D} = \hat{B A C} = 20^{\circ}$ (hai góc so le trong)

Trong tam giác $A C D$ , ta có: $\hat{D A C} = 180^{\circ} - (\hat{A C D} + \hat{D}) = 90^{\circ}$

b) Trong tứ giác $G H I K$ , ta có: $\hat{H} = 360^{\circ} - (\hat{K G H} + \hat{I} + \hat{K}) = 115^{\circ}$

Trong tam giác $G H E$ , ta có: $\hat{H E G} = 180^{\circ} - (\hat{E G H} + \hat{H}) = 40^{\circ}$

Vậy $\hat{G E I} = 180^{\circ} - \hat{H E G} = 140^{\circ}$

c) Trong tứ giác $M N P Q$ , ta có: $\hat{N P Q} = 360^{\circ} - (\hat{Q M N} + \hat{N} + \hat{Q}) = 70^{\circ}$

Do $P M$ là tia phân giác của góc $N P Q$ nên $\hat{N P M} = \hat{M P Q} = \frac{\hat{N P Q}}{2} = 35^{\circ}$

Trong tam giác $M P Q$ , ta có: $\hat{Q M P} = 180^{\circ} - (\hat{M P Q} + \hat{Q}) = 85^{\circ}$

Bài 9 trang 90 SBT Toán 8 Tập 1: Chứng minh rằng: Trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai cạnh đối.

Lời giải:

Gọi $O$ là giao điểm của hai đường chéo $A C$ và $B D$ trong tứ giác $A B C D$ .

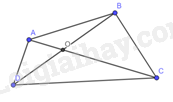
Sách bài tập Toán 8 Bài 2 (Cánh diều): Tứ giác (ảnh 6)

Xét tam giác $O A B$ , ta có: $O A + O B > A B$

Xét tam giác $O C D$ , ta có: $O C + O D > C D$

Suy ra $O A + O B + O C + O D > A B + C D$

Hay $A C + B D > A B + C D$

Tương tự ta cũng chứng minh được $A C + B D > A D + B C$

Vậy: Trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng độ dài hai cạnh đối.

Bài 10 trang 90 SBT Toán 8 Tập 1: Thả diều là một trò chơi dân gian của nhiều trẻ em ở Việt Nam cũng như ở nhiều nước trên thế giới. Một tứ giác $A B C D$ với $A B = A D, B C = C D$ gọi là hình “chiếc diều” (Hình 9)

a) So sánh $\hat{B}$ và $\hat{D}$ .

b) Tìm mối liên hệ giữa hai đường chéo $A C$ và $B D$

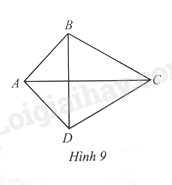
Sách bài tập Toán 8 Bài 2 (Cánh diều): Tứ giác (ảnh 7)

Lời giải:

Gọi $O$ là giao điểm của hai đường chéo $A C$ và $B D$

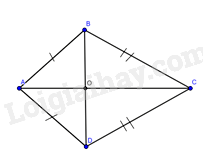
Sách bài tập Toán 8 Bài 2 (Cánh diều): Tứ giác (ảnh 8)

a) $Δ A B C = Δ A D C$ (c-c-c). suy ra $\hat{A B C} = \hat{A D C}$

b) $Δ A B C = Δ A D C$ nên $\hat{B A O} = \hat{D A O}$

$Δ A B O = Δ A D o$ . Suy ra $\hat{A O B} = \hat{A O D}$

Mà $\hat{A O D} + \hat{A O B} = 180^{\circ}$ nên $\hat{A O B} = \hat{A O D} = 90^{\circ}$

Vậy $A C ⊥ B D$ .

Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:

Bài 1: Định lí Pythagore

Bài 3: Hình thang cân

Bài 4: Hình bình hành

Bài 5: Hình chữ nhật

Bài 6: Hình thoi

Từ khóa :

Giải bài tập Toán 8

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

295

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

315

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

344

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

291

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.