Bài 27 trang 108 Toán 11 Tập 2 | Kết nối tri thức Giải Toán lớp 11

Bài 27 trang 108 Toán 11 Tập 2 | Kết nối tri thức Giải Toán lớp 11

Trần Thị Thùy Linh Ngày: 29-01-2024 Lớp 11

141

Với giải Bài 27 trang 108 SGK Toán 11 Kết nối tri thức chi tiết trong Toán 11 (Kết nối tri thức) Bài tập ôn tập cuối năm giúp học sinh dễ dàng xem và so sánh lời giải, từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Bài 27 trang 108 Toán 11 Tập 2 | Kết nối tri thức Giải Toán lớp 11

Bài 27 trang 108 Toán 11 Tập 2: Giải các phương trình và bất phương trình sau:

a) $3^{\frac{1}{x}}$ = 4;

b) $2^{x^{2} - 3 x}$ = 4;

c) log₄(x + 1) + log₄(x – 3) = 3;

d) ${(\frac{1}{5})}^{x^{2} - 2 x} \geq \frac{1}{125}$ ;

e) ${(2 - \sqrt{3})}^{x} \leq {(2 + \sqrt{3})}^{x + 2}$ ;

f) log (3x² + 1) > log (4x).

Lời giải:

a) Điều kiện: x ≠ 0.

Ta có $3^{\frac{1}{x}} = 4$ $\Leftrightarrow \frac{1}{x} = \log_{3} 4$ $\Leftrightarrow x = \frac{1}{\log_{3} 4} = \log_{4} 3$ (thỏa mãn).

Vậy nghiệm của phương trình là x = log₄3.

b) $2^{x^{2} - 3 x} = 4$ $\Leftrightarrow 2^{x^{2} - 3 x} = 2^{2}$ $\Leftrightarrow x^{2} - 3 x = 2$

$\Leftrightarrow x^{2} - 3 x - 2 = 0$ $\Leftrightarrow x = \frac{3 + \sqrt{17}}{2}$ hoặc $x = \frac{3 - \sqrt{17}}{2}$ .

Vậy tập nghiệm của phương trình là S = 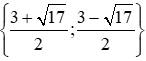Bài 27 trang 108 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11 .

c) Điều kiện 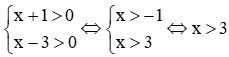Bài 27 trang 108 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11 .

Ta có log₄(x + 1) + log₄(x – 3) = 3

$\Leftrightarrow$ log₄ [(x + 1)(x – 3)] = 3

$\Leftrightarrow$ (x + 1)(x – 3) = 4³

$\Leftrightarrow$ x² – 2x – 67 = 0

$\Leftrightarrow$ x = 1 - 2 $\sqrt{17}$ (loại) hoặc x = 1 + 2 $\sqrt{17}$ (thỏa mãn).

Vậy nghiệm của phương trình là x = 1 + 2 $\sqrt{17}$ .

d) Ta có ${(\frac{1}{5})}^{x^{2} - 2 x} \geq \frac{1}{125}$ $\Leftrightarrow {(\frac{1}{5})}^{x^{2} - 2 x} \geq {(\frac{1}{5})}^{3}$

$\Leftrightarrow x^{2} - 2 x \leq 3$ $\Leftrightarrow x^{2} - 2 x - 3 \leq 0$ $\Leftrightarrow - 1 \leq x \leq 3$ .

Vậy tập nghiệm của bất phương trình là S = [−1; 3].

e) ${(2 - \sqrt{3})}^{x} \leq {(2 + \sqrt{3})}^{x + 2}$

$\Leftrightarrow$ Bài 27 trang 108 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11 $\leq {(2 + \sqrt{3})}^{x + 2}$

$\Leftrightarrow {(\frac{1}{2 + \sqrt{3}})}^{x} \leq {(2 + \sqrt{3})}^{x + 2}$

$\Leftrightarrow {(2 + \sqrt{3})}^{- x} \leq {(2 + \sqrt{3})}^{x + 2}$ .

Vậy tập nghiệm của bất phương trình là S = [−1; + $\infty$ ).

f) Điều kiện: 4x > 0 $\Leftrightarrow$ x > 0.

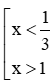
Ta có log (3x² + 1) > log (4x) $\Leftrightarrow$ 3x² + 1 > 4x $\Leftrightarrow$ 3x² – 4x + 1 > 0 $\Leftrightarrow$ Bài 27 trang 108 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11 .

Kết hợp với điều kiện, ta có 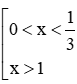Bài 27 trang 108 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11 .

Vậy tập nghiệm của bất phương trình là $S = (0; \frac{1}{3}) \cup (1; + \infty)$ .

Xem thêm Lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 1 trang 105 Toán 11 Tập 2: Khẳng định nào sau đây là sai...

Bài 2 trang 105 Toán 11 Tập 2: Khẳng định nào sau đây là đúng...

Bài 3 trang 105 Toán 11 Tập 2: Cho dãy số (u_n) với u_n = 5ⁿ. Số hạng u_2n bằng...

Bài 4 trang 105 Toán 11 Tập 2: Dãy số (u_n) cho bởi công thức số hạng tổng quát nào dưới đây là dãy số tăng...

Bài 5 trang 105 Toán 11 Tập 2: Khẳng định nào sau đây là sai?..

Bài 6 trang 105 Toán 11 Tập 2:Hàm số nào dưới đây không liên tục trên ℝ...

Bài 7 trang 105 Toán 11 Tập 2: Cho 0 < a ≠ 1. Giá trị của biểu thức ${log}_{a} (a^{3} \cdot \sqrt[4]{a}) + {(\sqrt[3]{a})}^{{log}_{a} 8}$ bằng...

Bài 8 trang 105 Toán 11 Tập 2: Cho đồ thị ba hàm số mũ y = a^x, y = b^x và y = c^x như trong hình vẽ dưới đây...

Bài 9 trang 106 Toán 11 Tập 2: Nếu f(x) = sin²x + xe^2x thì f"(0) bằng...

Bài 10 trang 106 Toán 11 Tập 2: Phương trình tiếp tuyến của đồ thị hàm số y = −2x³ + 6x² – 5 tại điểm M(3; −5) thuộc đồ thị là...

Bài 11 trang 106 Toán 11 Tập 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA $⊥$ (ABC), SA = a $\sqrt{2}$ ...

Bài 12 trang 106 Toán 11 Tập 2: Cho hình hộp ABCD.A'B'C'D' có đáy ABCD là hình chữ nhật. Biết AC = AA' = 2a...

Bài 13 trang 106 Toán 11 Tập 2: Cho tứ diện đều ABCD có cạnh bằng a. Gọi M, N lần lượt là trung điểm của cạnh AC và cạnh AD...

Bài 14 trang 106 Toán 11 Tập 2: Cho lăng trụ tam giác đều ABC.A'B'C' có AB = 1; AA' = 2. Thể tích khối lăng trụ ABC.A'B'C' bằng...

Bài 15 trang 106 Toán 11 Tập 2: Cho hình lập phương ABCD.A'B'C'D' có AC' = $\sqrt{3}$ . Khoảng cách giữa hai đường thẳng AB' và BC' bằng...

Bài 16 trang 106 Toán 11 Tập 2: Cho mẫu số liệu ghép nhóm về thu nhập của các công nhân tại một doanh nghiệp lớn:...

Bài 17 trang 106 Toán 11 Tập 2: Cho mẫu số liệu ghép nhóm về thu nhập của các công nhân tại một doanh nghiệp lớn:...

Bài 18 trang 106 Toán 11 Tập 2:Vận động viên Tùng thi bắn súng. Biết rằng xác suất để Tùng bắn trúng vòng 10 là 0,2...

Bài 19 trang 107 Toán 11 Tập 2: Hai bạn Sơn và Tùng, mỗi người gieo một con xúc xắc. Xác suất để số chấm xuất hiện...

Bài 20 trang 107 Toán 11 Tập 2: Hai bạn An và Bình tham gia một trò chơi độc lập với nhau. Xác suất để An và Bình...

Bài 21 trang 107 Toán 11 Tập 2: Rút gọn các biểu thức sau: a) $A = \frac{1 - 2 {sin}^{2} x}{1 + sin 2 x} - \frac{1 - tan x}{1 + tan x}$ ;...

Bài 22 trang 107 Toán 11 Tập 2: Mùa xuân ở hội Lim (tỉnh Bắc Ninh) thường có trò chơi đu. Khi người chơi đu nhún cây đu...

Bài 23 trang 107 Toán 11 Tập 2: Cho cấp số nhân (u_n) biết rằng ba số u₁, u₄ và u₇ lần lượt là các số hạng thứ nhất, thứ hai...

Bài 24 trang 107 Toán 11 Tập 2: Một công ty đề xuất kí hợp đồng với một người lao động theo một trong hai loại hợp đồng sau...

Bài 25 trang 108 Toán 11 Tập 2: Tính các giới hạn sau: a) $\lim_{n \to + \infty} \frac{1 + 3 + 5 + \dots + (2 n - 1)}{n^{2} + 2 n + 3}$ ;...

Bài 26 trang 108 Toán 11 Tập 2: Tìm các giá trị của tham số m để...

Bài 27 trang 108 Toán 11 Tập 2: Giải các phương trình và bất phương trình sau: a) $3^{\frac{1}{x}}$ = 4;...

Bài 28 trang 108 Toán 11 Tập 2: Để xác định tính acid và tính base của các dung dịch, người ta sử dụng khái niệm độ pH...

Bài 29 trang 108 Toán 11 Tập 2: Tính đạo hàm của các hàm số sau: a) $y = 3 x^{2} - 2 \sqrt{x}$ ;...

Bài 30 trang 108 Toán 11 Tập 2: Một chất điểm chuyển động có phương trình s(t) = t³ – 3t² – 9t + 2, ở đó thời gian t > 0...

Xem thêm Lời giải bài tập Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 32: Các quy tắc tính đạo hàm

Bài 33: Đạo hàm cấp hai

Bài tập cuối chương 9 trang 97

Một vài mô hình toán học sử dụng hàm số mũ và hàm số lôgarit

Hoạt động thực hành trải nghiệm Hình học

Từ khóa :

Giải bài tập Toán 11

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

224

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

261

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

282

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

233

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.