Lũy thừa (Lý thuyết + 50 bài tập có lời giải) 

A. Tóm tắt lý thuyết

1. Định nghĩa lũy thừa và căn

    • Cho số thực b và số nguyên dương n (n ≥ 2) . Số a được gọi là căn bậc n của số b nếu aⁿ = b .

    • Chú ý: - Với n lẻ và b ∈ R : Có duy nhất một căn bậc n của b, kí hiệu là ⁿ√b .

    - Với n chắn:

        +) b < 0: Không tồn tại căn bậc n của b.

        +) b = 0: Có một căn bậc n của b là số 0.

        +) b > 0: Có hai căn bậc n của a là hai số đối nhau, căn có giá trị dương ký hiệu là ⁿ√b, căn có giá trị âm kí hiệu là -ⁿ√b.

Số mũ α	Cơ số a	Lũy thừa aα
α = n ∈ N*	a ∈ R	aα = an = a.a. ... .a (n thừa số a)
α = 0	a ≠ 0	aα = a0 = 1
α = -n (n ∈ N*)	a ≠ 0	aα = a0 = 1/an
α = m/n	a > 0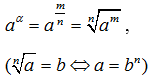
α = lim rn (rn ∈ Q, n ∈ N*)	a > 0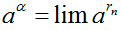

2. Một số tính chất của lũy thừa

    • Giả thuyết rằng mỗi biểu thức được xét đều có nghĩa:

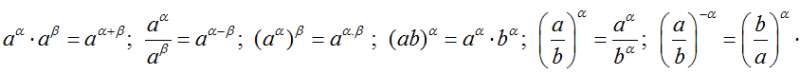
    • Nếu a > 1 thì a^α > a^β ⇔ α > β ; Nếu ) < a < 1 thì a^α > a^β ⇔ α < β .

    • Với mọi 0 < a < b, ta có: a^m < b^m ⇔ m > 0; a^m > b^m ⇔ m < 0 ;

    • Chú ý: - Các tính chất trên đúng trong trường hợp số mũ nguyên hoặc không nguyên.

    - Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số a phải khác 0.

    - Khi xét lũy thừa với số mũ không nguyên thì cơ số a phải dương.

3. Một số tính chất của căn bậc n

    • Với a, b ∈ R; n ∈ N*, ta có:

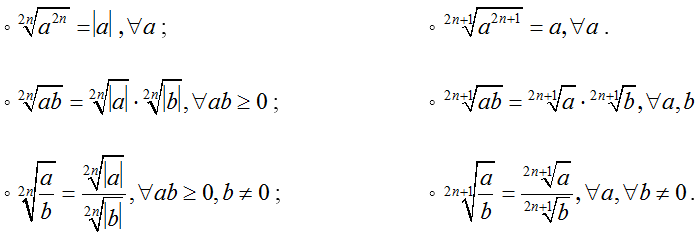
    • Với a, b ∈ R ta có:

    , ∀ a > 0, n nguyên dương, m nguyên

    , ∀ a ≥ 0, n, m nguyên dương

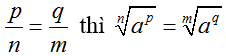    , ∀ a > 0, m,n nguyên dương, p, q nguyên. Đặc biệt 

B. Bài tập trắc nghiệm

Bài 1: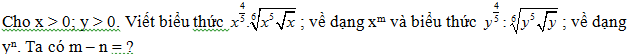 

Lời giải:

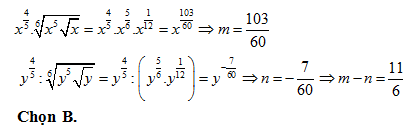
Bài 2: Viết biểu thức 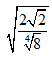 về dạng 2^x và biểu thức  về dạng 2^y. Ta có x² + y² = ?

Lời giải:

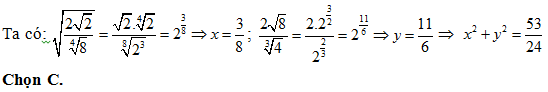
Bài 3: Đơn giản biểu thức 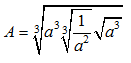 ta được:

Lời giải:

Ta có:

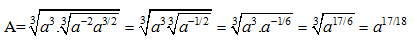
Chọn B.

Bài 4: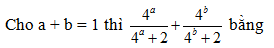

A. 4.       B.2.       C.3.       D. 1.

Lời giải:

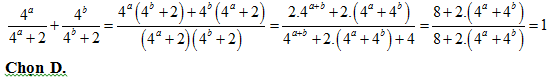
Bài 5: Đơn giản biểu thức 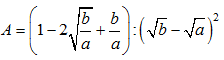 ta được:

A. A = a – b       B. A = a       C.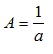       D. A = a + b

Lời giải:

Ta có:

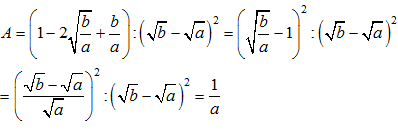
Chọn C.

Bài 6: Biết 4^x + 4^-x = 23 tính giá trị của biểu thức P = 2^x + 2^-x :

Lời giải:

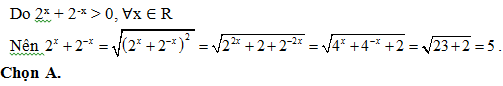
Bài 7: Đơn giản biểu thức: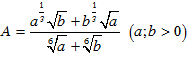 ta được:

Lời giải:

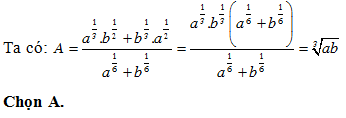
Bài 8: Đặt log₂ 3 = a, b = log₃ 5. Hãy biểu diễn log₁₂ 15 theo a và b

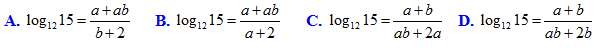
Lời giải:

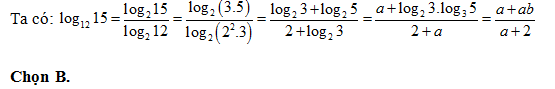
Bài 9: Đặt a = log₂ 3, b = log₅ 3. Hãy biểu diễn log₆ 45 theo a và b

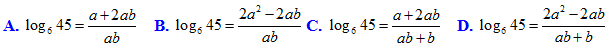
Lời giải:

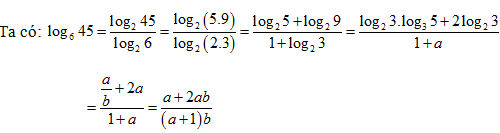
Chọn C.

Bài 10: Cho a = log₃ 5; b = log₇ 5. Khi đó khẳng định nào sau đây đúng?

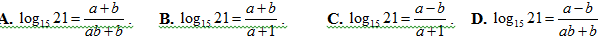
Lời giải:

Bài 11: Cho log₂ 3 = a, log₃ 5 = b. Khi đó log₁₂ 90 tính theo a, b bằng:

Lời giải:

Phương pháp: Biến đổi linh hoạt công thức logarit

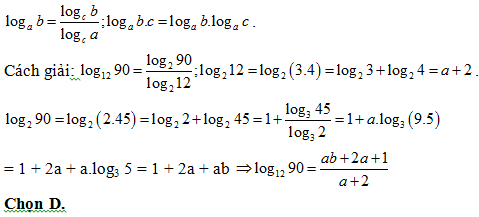
Bài 12: Cho log₅ 3 = a, log₅ 5 = b. Tính log₁₅ 105 theo a và b.

Lời giải:

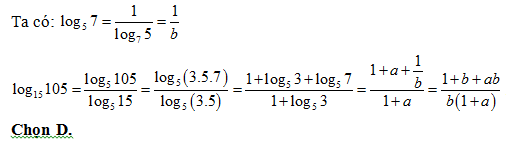
Bài 13: Cho a = log₃ 2 và b = log₃ 5. Tính log₁₀ 60 theo a và b.

Lời giải:

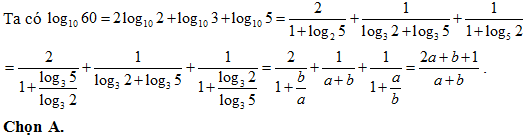
Bài 14: Nếu log₈ 3 = p và log₃ 5 = q thì log 5 bằng:

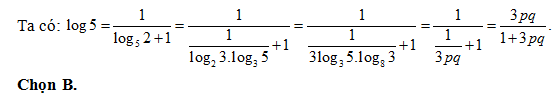
Lời giải:

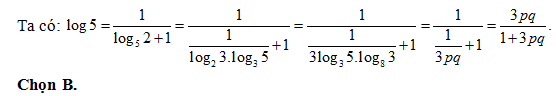
Bài 15: Biết log₂₇ 5 = a, log₈ 7 = b, log₂ 3 = c thì log₁₂ 35 tính theo a, b, c bằng:

Lời giải:

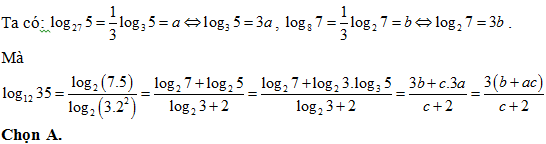
Bài 16: Cho log₂ 3 = a, log₃ 5 = b, log₇₂ = c. Hãy tính log₂ 63 theo a, b, c

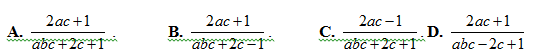
Lời giải:

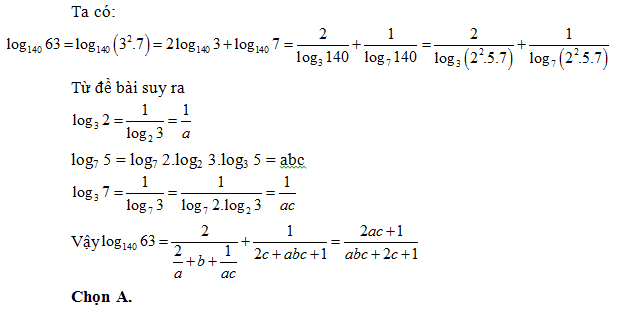
Bài 17: Cho log_b a = x và log_b c = y. Hãy biểu diễn 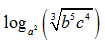 theo x và y:

Lời giải:

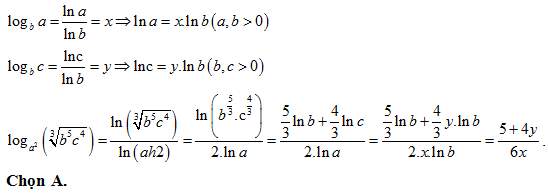
Bài 18: Cho 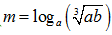 , với a > 1, b > 1 và P = log_a²b + 16log_b a. Tìm m sao cho P đạt giá trị nhỏ nhất.

Lời giải:

Bài 19: Cho log₂ 6 = a và log₃ 5 = b. Hãy tính 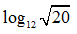 theo a, b

Lời giải:

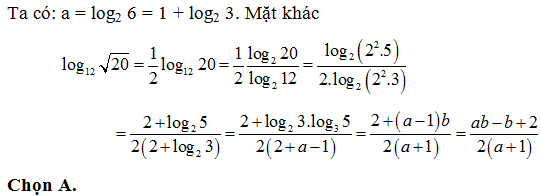
Bài 20:

Lời giải:

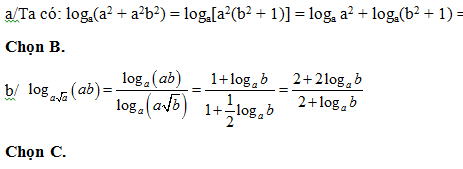
Bài 21: Cho các số thực dương x; y > 0 thỏa mãn x² + y² = 8xy. Khẳng định nào sau đây là đúng ?

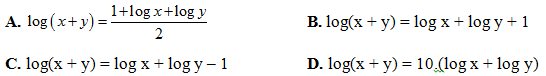
Lời giải:

Ta có: x² + y² = 8xy ⇔ (x + y)² = 10xy ⇒ log(x + y)² = log(10xy)

⇔ 2log(x + y) = 1 + log x + log y

Chọn B.

Bài 22: Cho các số thực dương x; y > 0 thỏa mãn x² + y² = 14xy. Khẳng định nào sau đây là đúng ?

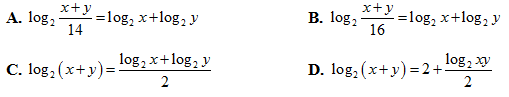
Lời giải:

Ta có: x² + y² = 14xy ⇔ (x + y)² = 16xy ⇔ log₂(x + y)² = log₂(16xy)

Chọn D.

Bài 23: Cho các số x, y ∈ R và x² + y² = 3xy. Khẳng định nào sau đây là đúng

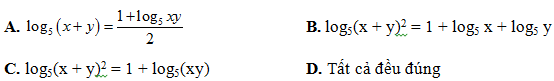
Lời giải:

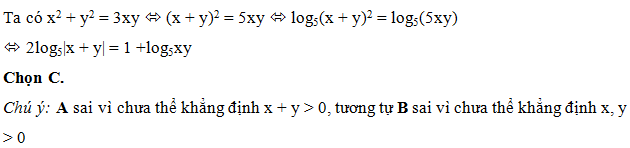
Bài 24:Cho log_a x = p; log_b x = q; log_c x = r (1 ≠ a,b,c; x > 0). Hãy tính log_abc x

Lời giải:

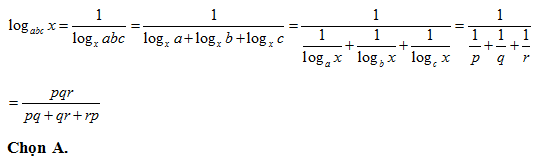
Bài 25: Rút gọn biểu thức : A = (log_b³a + 2log_b²a + log_b a)(log_a b – log_ab b) – log_b a là:

A. 0       B. 1       C. 3       D. 2

Lời giải:

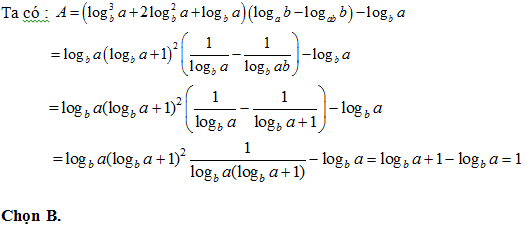
Bài 26: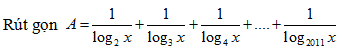 

A. A = log_x 2012!       B. A = log_x 1002!       C. A = log_x 2011!       D. A = log_x 2011.

Lời giải:

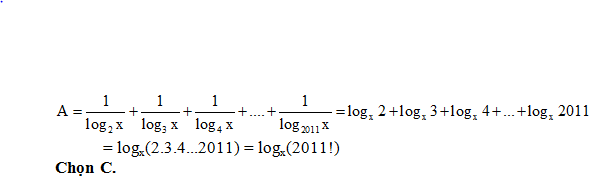
Bài 27: Cho a > 0, b > 0, Nếu viết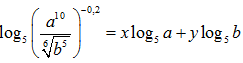 thì xy bằng bao nhiêu ?

Lời giải:

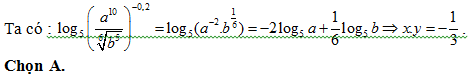
Bài 28: Kết quả rút gọn của biểu thức 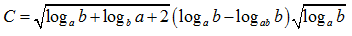 là:

Lời giải:

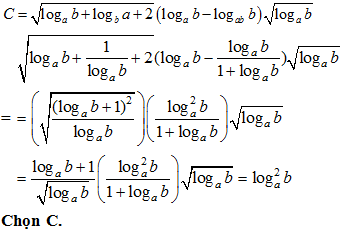
Bài 29: Thu gọn biểu thức 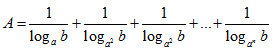 ta được:

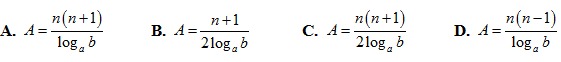
Lời giải:

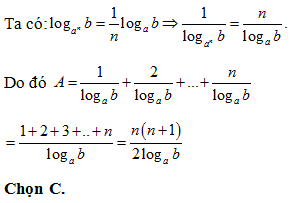
Bài 30:

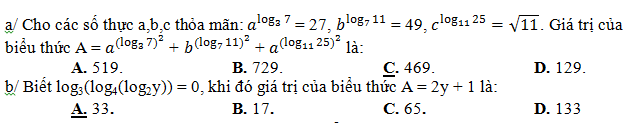
Lời giải:

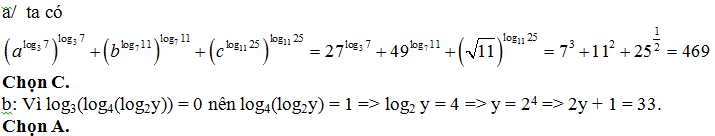
Bài 31: Tính giá trị của biểu thức P = ln(tan1º) +ln(tan2º) + ln(tan3º) + … + ln(tan89º).

Lời giải:

P = ln(tan1º) +ln(tan2º) + ln(tan3º) + … + ln(tan89º)

= ln(tan1º.tan2º.tan3º…tan89º)

= ln(tan1º.tan2º.tan3º…tan45º.cot44º.cot43º…cot1º)

= ln(tan45º) = ln 1 = 0 (vì tanα.cotα =1)

Chọn C.

Bài 32: Cho x, y là các số thực lớn hơn 1 thoả mãn x² + 9y² = 6xy. Tính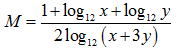 

Lời giải:

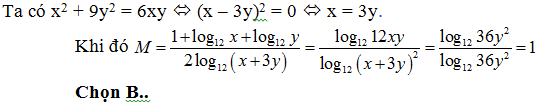
Bài 33: Cho f(1) = 1; f(m + n) = f(m) + f(n) + m.n, ∀m,n∈ R*. Khi đó giá trị của biểu

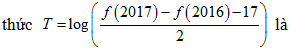
A. 4.    B. 4.    C. 6.     D. 9.

Lời giải:

Áp dụng hệ thức f(m + n) = f(m) + f(n) + m.n

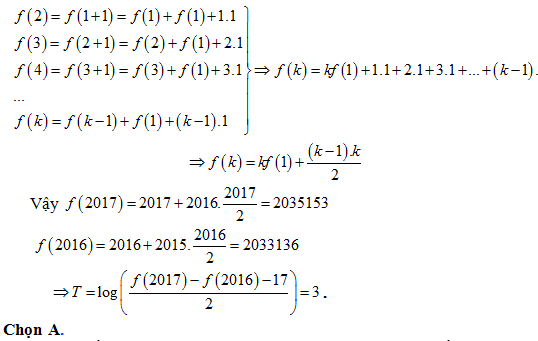
Bài 34: Xét các số thực a, b thỏa mãn a, b > 1. Tìm giá trị nhỏ nhất P_min của biểu thức

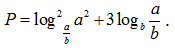
A. P_min = 19.         B. P_min = 13.         C. P_min = 14.         D. P_min = 15.

Lời giải:

Bài 35: Cho log9 x = log12 y = log16(x + y). Giá trị của tỉ số 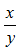 là:

Lời giải:

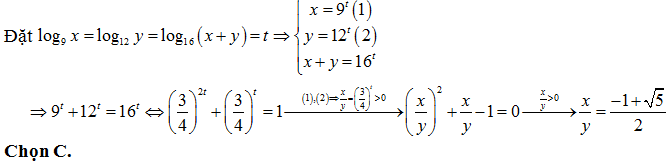
Bài 36: Cho x, y > 0 thỏa mãn log₂ x + log₂ y = log₄(x + y). Tìm x, y để biểu thức P = x² + y² đạt giá trị nhỏ nhất.

Lời giải:

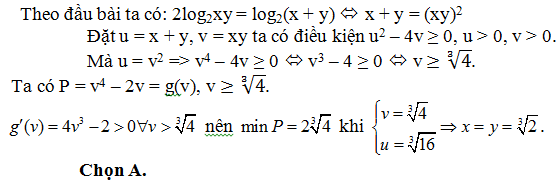
Bài 37: Cho 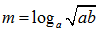 với a, b > 1 và P = log_a² b + 54log_a a. Khi đó giá trị của m để đạt giá trị nhỏ nhất là?

A. 2.       B. 3.       C. 4.       D. 5.

Lời giải:

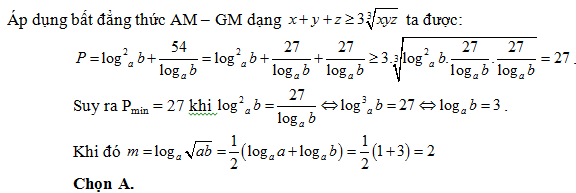
Bài 38: Cho a, b, c lần lượt là độ dài của hai cạnh góc vuông và cạnh huyền của một tam giác vuông, trong đó c – b ≠ 1; c + b ≠ 1. Khi đó log_c+b a + log_c-b a bằng:

A. -2log_c+ba.log_c-ba.

B.3log_c+ba.log_c-ba.

C.2log_c+ba.log_c-ba.

D.-3log_c+ba.log_c-ba.

Lời giải:

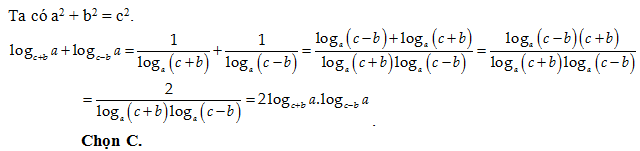
Bài 39: Cho hai số thực a, b với 1 < a < b. Khẳng định nào sau đây là khẳng định đúng?

A. log_a b < 1 < log_b a.

B. 1 < log_a b < log_b a.

C. log_a b < log_b a < 1.

D. log_ba < 1 < log_a b

Lời giải:

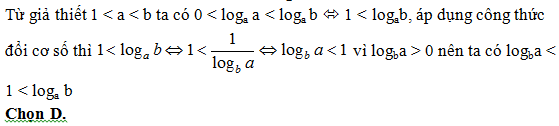
Bài 40: Cho a > 0; b > 0 thỏa mãn a² + b² = 7ab. Chọn mệnh đề đúng trong các mệnh đề sau?

Lời giải:

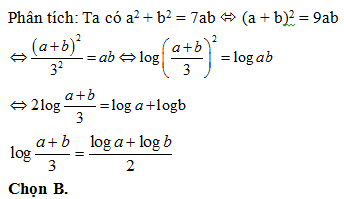
Bài 41: Cho x, y, z là các số thực dương tùy ý khác 1 và xyz khác 1. Đặt a = log_x y, b = log_z y. Mệnh đề nào sau đây đúng?

Lời giải:

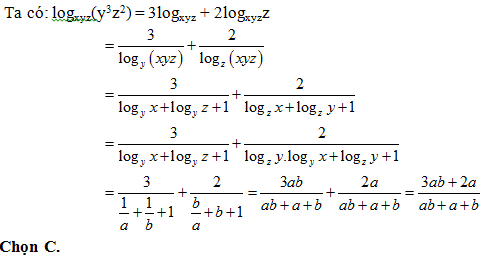
Bài 42: Cho các số dương a, b thõa mãn 4a² + 9b² = 13ab. Chọn câu trả lời đúng.

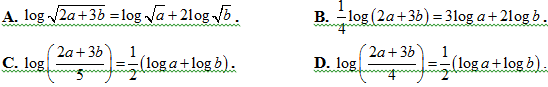
Lời giải:

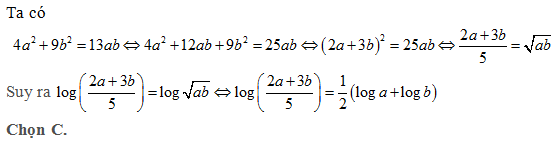
Bài 43: Cho x, y > 0 và x² + 4y² = 12xy. Khẳng định nào sau đây là khẳng định đúng?

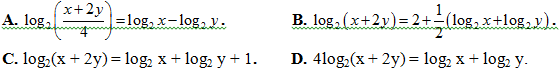
Lời giải:

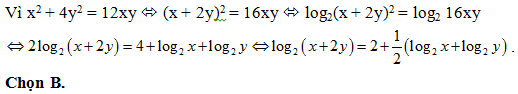
Bài 44: Cho a, b, c > 0 đôi một khác nhau và khác 1, khẳng định nào sau đây là khẳng định đúng?

Lời giải:

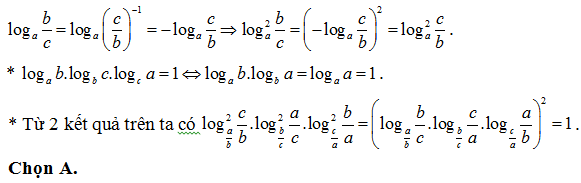
Bài 46: Cho a, b là các số thực dương thoả mãn a² + b² = 14ab. Khẳng định nào sau đây là sai ?

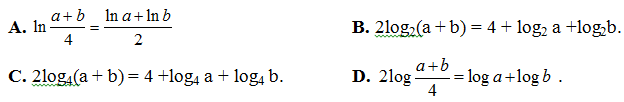
Lời giải:

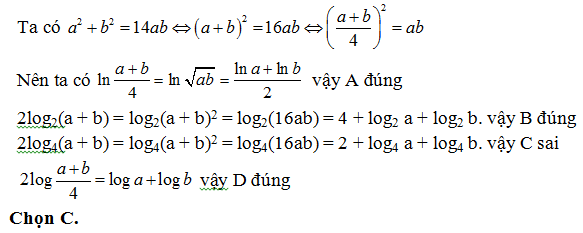
Bài 47: Với giá trị nào của m thì biểu thức 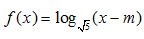 xác định với mọi x ∈ (-3;+∞)?

A.m >-3       B.m < 3       C. m ≤ -3.       D. m ≥ -3.

Lời giải:

Biểu thức f(x) xác định khi x-m>0 hay x>m.

Để f(x) xác định với mọi x ∈ (-3;+∞) thì m ≤ -3

Chọn C.

Bài 48: Biểu thức ln(x² – 2mx + 4) có nghĩa với mọi x ∈ R khi

Lời giải:

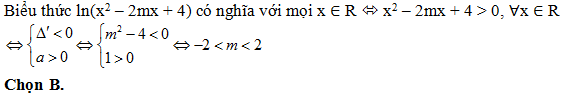
Bài 49: Tìm x để ba số ln2, ln(2^x – 1), ln(2^x + 3) theo thứ tự lập thành cấp số cộng.

A. 1.       B. 2.       C.log₂ 5       D.log₂ 3.

Lời giải:

Để ba số ln2, ln(2^x – 1), ln(2^x + 3) theo thứ tự lập thành cấp số cộng thì

2ln(2^x – 1) = ln2 + ln(2^x + 3) => (2^x – 1)² = 2(2^x + 3)

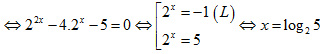
Chọn C.

Bài 50:

a/ Biểu thức T = log₂(ax² – 4x + 1) có nghĩa với mọi x ∈ R khi

A.0 < a < 4.       B. a > 0       C. a > 4       D. a ∈∅.

b/ Với giá trị nào của m thì biểu thức f(x) = 12 + 3log₂(3x + m) xác định với mọi x ∈ (3;+∞)?

A.m > -3.       B.m > -9.       C.m < -9.       D.m ≥ -3.

Lời giải: