SBT Toán 7 Kết nối tri thức: Ôn tập chương VII

Giang Ngày: 01-02-2023 Lớp 7

1.1 K

Toptailieu biên soạn và giới thiệu giải sách bài tập Toán 7 Ôn tập chương VII sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 7 Ôn tập chương VII.

Giải SBT Toán 7 (Kết nối tri thức): Ôn tập chương VII

Câu hỏi 1 trang 35 sách bài tập Toán 7: Biểu thức nào sau đây không là đa thức một biến?

A. $\sqrt{3}$

B.-x

C. $x + \frac{- 1}{x}$

D. $\frac{x}{\sqrt{2}} - 1$

Phương pháp giải

Đa thức một biến là tổng của những đơn thức có cùng một biến; mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.

Lời giải

Chọn C

Câu hỏi 2 trang 35 sách bài tập Toán 7: Cho đa thức G(x) = 4x³ + 2x² - 5x. Hệ số cao nhất và hệ số tự do của G(x).

A.4 và 0	B. 0 và 4
C.4 và -5	D.-5 và 4

Phương pháp giải

-Hệ số của hạng tử có bậc cao nhất gọi là hệ số cao nhất;

-Hệ số của hạng tử có bậc 0 (hạng tử không chứa biến) gọi là hệ số tự do.

Lời giải

Chọn A

Câu hỏi 3 trang 35 sách bài tập Toán 7: Cho hai đa thức f(x) và g(x) khác đa thức không sao cho tổng f(x) + g(x) khác đa thức không. Khi nào thì bậc của f(x) + g(x) chắc chắn bằng bậc của f(x)?

A.f(x) và g(x) có cùng bậc	B.f(x) có bậc lớn hơn bậc của g(x)
B.g(x) có bậc lớn hơn bậc của f(x)	D.Không bao giờ

Phương pháp giải

Cho một đa thức khác đa thức không. Trong dạng thu gọn của nó:

Bậc của hạng tử có bậc cao nhất gọi là bậc của đa thức

Lời giải

Chọn B

Câu hỏi 4 trang 35 sách bài tập Toán 7: Cho đa thức P(x) - x² + 5x - 6. Khi đó:

A. P(x) chỉ có một nghiệm là x = 1.

B. P(x) không có nghiệm

C. P(x) chỉ có một nghiệm là x = - 6.

D. x = 1 và x = - 6 là hai nghiệm của P(x).

Phương pháp giải

Giá trị x làm P(x) = 0 được gọi là nghiệm của đa thức.

Lời giải

Xét $P (x) = x^{2} + 5 x - 6 = 0$

$\Leftrightarrow x^{2} - x + 6 x - 6 = 0 \Leftrightarrow x (x - 1) + 6 (x - 1) = 0 \Leftrightarrow (x - 1) (x + 6) = 0$

$\Leftrightarrow x - 1 = 0$ hoặc $x + 6 = 0$

$\Leftrightarrow x = 1$ hoặc $x = - 6$

Chọn D

Câu hỏi 5 trang 35 sách bài tập Toán 7: Phép chia đa thức 2x⁵ - 3x⁴ + x³ - 6x² cho đa thức 5x^{7 - 2n} (n thuộc N; )<= n<= 3 là phép chia hết nếu:

A.n = 0

B. n = 1

C. n = 2

D. n = 3

Lời giải

Phép chia đa thức $2 x^{5} - 3 x^{4} + x^{3} - 6 x^{2}$ cho đa thức $5 x^{7 - 2 n} (n \in N; 0 \leq n \leq 3)$ khi $x^{2}$ chia hết cho $x^{7 - 2 n}$

$\Leftrightarrow 2 \geq 7 - 2 n \Leftrightarrow n \geq \frac{5}{2}$ .

Do đó, n = 3

Chọn D

Bài 7.34 trang 35 sách bài tập Toán 7: Thu gọn và sắp xếp các đa thức sau theo luỹ thừa giảm dần của biến. Tìm bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức đó.

a) $x^{5} + 7 x^{2} - x - 2 x^{5} + 3 - 5 x^{2};$

b) $4 x^{3} - 5 x^{2} + x - 4 x^{3} + 3 x^{2} - 2 x + 6$ .

Phương pháp giải

-Rút gọn đa thức

-Bậc: bậc của hạng tử có bậc cao nhất gọi là bậc của đa thức

-Hệ số cao nhất: Hệ số của hạng tử có bậc cao nhất.

-Hệ số tự do: Hệ số của hạng tử không chứa biến x.

Lời giải

$\begin{array}{l} x^{5} + 7 x^{2} - x - 2 x^{5} + 3 - 5 x^{2} \\ = (x^{5} - 2 x^{5}) + (7 x^{2} - 5 x^{2}) - x + 3 \\ = - x^{5} + 2 x^{2} - x + 3 \end{array}$

Bậc: 5

Hệ số cao nhất: -1

Hệ số tự do: 3

$\begin{array}{l} 4 x^{3} - 5 x^{2} + x - 4 x^{3} + 3 x^{2} - 2 x + 6 \\ = (4 x^{3} - 4 x^{3}) + (- 5 x^{2} + 3 x^{2}) + (x - 2 x) + 6 \\ = - 2 x^{2} - x + 6 \end{array}$

Bậc: 2

Hệ số cao nhất: -2

Hệ số tự do: 6.

Bài 7.35 trang 35 sách bài tập Toán 7: Cho 2 đa thức f(x) = 4x⁴ - 5x³ +3x +2 và g(x) = -4x⁴ + 5x³ + 7. Trong các số -4; -3; 0 và 1, số nào là nghiệm của đa thức f(x)+g(x)?

Phương pháp giải

-Tính tổng $f (x) + g (x)$

-Tìm nghiệm: Cho $f (x) + g (x) = 0$

Lời giải

$\begin{array}{l} f (x) + g (x) \\ = (4 x^{4} - 5 x^{3} + 3 x + 2) + (- 4 x^{4} + 5 x^{3} + 7) \\ = (4 x^{4} - 4 x^{4}) + (- 5 x^{3} + 5 x^{3}) + 3 x + (2 + 7) \\ = 3 x + 9 \end{array}$

$\begin{array}{l} f (x) + g (x) = 0 \\ \Rightarrow 3 x + 9 = 0 \\ \Rightarrow 3 x = - 9 \\ \Rightarrow x = - 9 : 3 \\ \Rightarrow x = - 3 \end{array}$

Vậy đa thức $f (x) + g (x)$ có nghiệm là x = 3

Bài 7.36 trang 35 sách bài tập Toán 7: Cho hai đa thức f(x) = - x⁵ + 3x² + 4x + 8; g(x) = - x⁵ - 3x² + 4x + 2. Chứng minh rằng đa thức f(x) - g(x) không có nghiệm.

Phương pháp giải

-Rút gọn $f (x) - g (x)$

-Chứng minh $f (x) - g (x) > 0$ , với mọi x.

Lời giải

Ta có:

$\begin{array}{l} f (x) - g (x) \\ = (- x^{5} + 3 x^{2} + 4 x + 8) - (- x^{5} - 3 x^{2} + 4 x + 2) \\ = - x^{5} + 3 x^{2} + 4 x + 8 + x^{5} + 3 x^{2} - 4 x - 2 \\ = (- x^{5} + x^{5}) + (3 x^{2} + 3 x^{2}) + (4 x - 4 x) + (8 - 2) \\ = 6 x^{2} + 6 \end{array}$

Mà

$\begin{array}{l} x^{2} \geq 0 \Rightarrow 6 x^{2} \geq 0 \Rightarrow 6 x^{2} + 6 > 0 \\ \Rightarrow f (x) - g (x) > 0 \end{array}$

Do đó $f (x) - g (x)$ không có nghiệm.

Bài 7.37 trang 35 sách bài tập Toán 7: Cho hai đa thức sau: P(x) = 3x⁵ = 2x⁴ + 7x² + 3x - 10; Q(x) = - 3x⁵ - x³ - 7x² + 2x + 10.

a)Xác định bậc, hệ số cao nhất và hệ số tự do của các đa thức:

$S (x) = P (x) + Q (x); D (x) = P (x) - Q (x)$ .

b)Trong tập hợp {-1; 0; 1}, tìm những số là nghiệm của một trong hai đa thức S(x) và D(x).

Phương pháp giải

-Rút gọn đa thức

-Bậc: bậc của hạng tử có bậc cao nhất gọi là bậc của đa thức

-Hệ số cao nhất: Hệ số của hạng tử có bậc cao nhất.

-Hệ số tự do: Hệ số của hạng tử không chứa biến x.

Thay x = -1; x = 0; x = 1 vào các đa thức S(x) và D(x).

Lời giải

$\begin{array}{l} S (x) = P (x) + Q (x) \\ = (3 x^{5} - 2 x^{4} + 7 x^{2} + 3 x - 10) + (- 3 x^{5} - x^{3} - 7 x^{2} + 2 x + 10) \\ = (3 x^{5} - 3 x^{5}) - 2 x^{4} - x^{3} + (7 x^{2} - 7 x^{2}) + (3 x + 2 x) + (- 10 + 10) \\ = - 2 x^{4} - x^{3} + 5 x \end{array}$

Bậc: 4

Hệ số cao nhất: -2

Hệ số tự do: 0

$\begin{array}{l} D (x) = P (x) - Q (x) \\ = (3 x^{5} - 2 x^{4} + 7 x^{2} + 3 x - 10) - (- 3 x^{5} - x^{3} - 7 x^{2} + 2 x + 10) \\ = (3 x^{5} + 3 x^{5}) - 2 x^{4} + x^{3} + (7 x^{2} + 7 x^{2}) + (3 x - 2 x) + (- 10 - 10) \\ = 6 x^{5} - 2 x^{4} + x^{3} + 14 x^{2} + x - 20 \end{array}$

Bậc: 5

Hệ số cao nhất: 6

Hệ số tự do: -20

Ta có:

$\begin{array}{l} S (- 1) = - 2. {(- 1)}^{4} - {(- 1)}^{3} + 5. (- 1) = - 2 + 1 - 5 = - 6 \neq 0 \\ S (0) = - 2.0 - 0 + 5.0 = 0 \\ S (1) = - 2 - 1 + 5 = 2 \neq 0 \end{array}$

Vậy S(x) có nghiệm x = 0.

Lại có:

$\begin{array}{l} D (- 1) = - 6 - 2 - 1 + 14 - 1 - 20 = - 16 \neq 0 \\ D (0) = 0 - 0 + 0 + 0 + 0 - 20 = - 20 \neq 0 \\ D (1) = 6 - 2 + 1 + 14 + 1 - 20 = 0 \end{array}$

Vậy D(x) có nghiệm x = 1

Bài 7.38 trang 35 sách bài tập Toán 7: Biết rằng đa thức f(x) = x⁴ +px³ - 2x² +1 có 2 nghiệm (khác 0) là hai số đối nhau. Chứng minh rằng p = 0.

Phương pháp giải

- Gọi 2 nghiệm đối nhau của f(x) là a và -a (a $\neq$ 0).

-Tính f(a); f(-a)

-Có f(a) = 0 = f(-a). Tìm p

Lời giải

Gọi 2 nghiệm đối nhau của f(x) là a và -a (a $\neq$ 0). Khi đó ta có:

$\begin{array}{l} f (a) = a^{4} + p a^{3} - 2 a^{2} + 1 \\ f (- a) = {(- a)}^{4} + p {(- a)}^{3} - 2 {(- a)}^{2} + 1 = a^{4} - p a^{3} - 2 a^{2} + 1 \\ f (a) = f (- a) \\ \Rightarrow a^{4} + p a^{3} - 2 a^{2} + 1 = a^{4} - p a^{3} - 2 a^{2} + 1 \\ \Rightarrow p a^{3} = - p a^{3} \\ \Rightarrow 2 p a^{3} = 0 \\ D o a \neq 0 \Rightarrow p = 0 \end{array}$

Bài 7.39 trang 35 sách bài tập Toán 7: Thực hiện các phép tính sau: a) (5x³ - 2x² + 4x - 4)(3x² +x - 1)

$b) (9 x^{5} - 6 x^{3} + 18 x^{2} - 35 x - 42) : (3 x^{3} + 5 x + 6);$

$c) [(6 x^{3} - 5 x^{2} - 8 x + 5) - (4 x^{2} - 6 x + 2)] : (2 x - 3) .$

Phương pháp giải

a)Thực hiện nhân đa thức với đa thức: (A+B)(C+D) = AC + AD + BC + BD.

b)Thực hiện chia đa thức: đặt tính chia

Lời giải

$\begin{array}{l} a) \\ (5 x^{3} - 2 x^{2} + 4 x - 4) (3 x^{2} + x - 1) \\ = 15 x^{5} + 5 x^{4} - 5 x^{3} - 6 x^{4} - 2 x^{3} + 2 x^{2} + 12 x^{3} + 4 x^{2} - 4 x - 12 x^{2} - 4 x + 4 \\ = 15 x^{5} + (5 x^{4} - 6 x^{4}) + (- 5 x^{3} - 2 x^{3} + 12 x^{3}) + (2 x^{2} + 4 x^{2} - 12 x^{2}) + (- 4 x - 4 x) + 4 \\ = 15 x^{5} - x^{4} + 5 x^{3} - 6 x^{2} - 8 x + 4 \end{array}$

Mẹ cho Quỳnh 100 nghìn đồng. Quỳnh mua một bộ dụng cụ học tập (ảnh 1)

$\begin{array}{l} (6 x^{3} - 5 x^{2} - 8 x + 5) - (4 x^{2} - 6 x + 2) \\ = 6 x^{3} + (- 5 x^{2} - 4 x^{2}) + (- 8 x + 6 x) + (5 - 2) \\ = 6 x^{3} - 9 x^{2} - 2 x + 3 \end{array}$

Đặt tính chia:

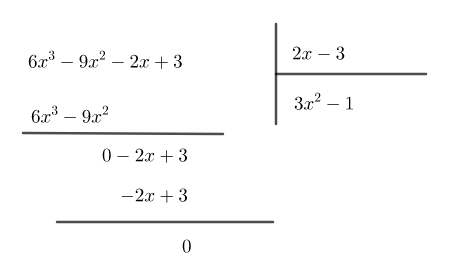
Mẹ cho Quỳnh 100 nghìn đồng. Quỳnh mua một bộ dụng cụ học tập (ảnh 2)

Bài 7.40 trang 35 sách bài tập Toán 7: Rút gọn các biểu thức sau: a) A = (x-1)(x+2)(x-3) - (x+1)(x-2)(x+3)

b) $B = (x - 1) (x + 1) (x^{2} + 1) (x^{4} + 1) - x^{8} .$

Phương pháp giải

Tách riêng tính $(x - 1) (x + 2) (x - 3)$ và $(x + 1) (x - 2) (x + 3)$ : nhân các tích theo thứ tự từ trái qua phải

b)Chứng minh công thức: $(A - 1) (A + 1) = A^{2} - 1$ .

Lời giải

Ta có:

$\begin{array}{l} (x - 1) (x + 2) (x - 3) \\ = (x^{2} + 2 x - x - 2) (x - 3) \\ = (x^{2} + x - 2) (x - 3) \\ = x^{3} - 3 x^{2} + x^{2} - 3 x - 2 x + 6 \\ = x^{3} - 2 x^{2} - 5 x + 6 \end{array}$

$\begin{array}{l} (x + 1) (x - 2) (x + 3) \\ = (x^{2} - x - 2) (x + 3) \\ = x^{3} + 3 x^{2} - x^{2} - 3 x - 2 x - 6 \\ = x^{3} + 2 x^{2} - 5 x - 6 \end{array}$

$\begin{array}{l} \Rightarrow A = (x^{3} - 2 x^{2} - 5 x + 6) - (x^{3} + 2 x^{2} - 5 x - 6) \\ = (x^{3} - x^{3}) + (- 2 x^{2} - 2 x^{2}) + (- 5 x + 5 x) + (6 + 6) \\ = - 2 x^{2} + 12 \end{array}$

Với X là một biểu thức tuỳ ý, ta có:

$(A - 1) (A + 1) = A^{2} - A + A - 1 = A^{2} - 1$

Áp dụng:

$\begin{array}{l} (x - 1) (x + 1) (x^{2} + 1) (x^{4} + 1) - x^{8} \\ = (x^{2} - 1) (x^{2} + 1) (x^{4} + 1) - x^{8} \\ = [{(x^{2})}^{2} - 1] . (x^{4} + 1) - x^{8} \\ = (x^{4} - 1) (x^{4} + 1) - x^{8} \\ = [{(x^{4})}^{2} - 1] - x^{8} \\ = x^{8} - 1 - x^{8} \\ = - 1 \end{array}$