SBT Toán 7 Cánh diều Bài 3: Giá trị tuyệt đối của một số thực

Nguyễn Thanh Huyền Ngày: 02-02-2023 Lớp 7

745

Toptailieu biên soạn và giới thiệu giải sách bài tập Toán 7 Bài 3 (Cánh diều): Giá trị tuyệt đối của một số thực hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 7 Bài 3.

Giải sách bài tập Toán 7 Bài 3 (Cánh diều): Giá trị tuyệt đối của một số thực

Bài 19 trang 45 sách bài tập Toán 7: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? Vì sao?

a) Giá trị tuyệt đối của một số thực là một số dương hoặc bằng 0.

b) Hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau.

c) Hai số đối nhau có giá trị tuyệt đối bằng nhau.

d) Giá trị tuyệt đối của một số thực luôn bằng chính nó.

Lời giải:

a) Phát biểu này đúng. Vì giá trị tuyệt đối của một số thực là một số không âm.

b) Phát biểu này sai. Vì hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc là hai số đối nhau.

c) Phát biểu này đúng. Vì hai số đối nhau có điểm biểu diễn cách đều điểm gốc 0 nên chúng có giá trị tuyệt đối bằng nhau.

d) Phát biểu này sai. Vì giá trị tuyệt đối của số âm là số đối của nó.

Bài 20 trang 45 sách bài tập Toán 7: Tìm:

(ảnh 1)

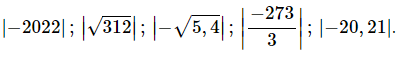
Lời giải:

$| - 2 022 | = - (- 2 022) = 2 022$ ;

$| \sqrt{312} | = \sqrt{312}$ ;

$| - \sqrt{5, 4} | = - (- \sqrt{5, 4}) = \sqrt{5, 4}$ ;

$| \frac{- 273}{3} | = - (\frac{- 273}{3}) = \frac{273}{3}$ ;

$| - 20, 21 | = - (- 20, 21) = 20, 21$ .

Bài 21 trang 45 sách bài tập Toán 7: Biểu diễn trên trục số giá trị tuyệt đối của mỗi số đã cho trên trục số ở Hình 3:

Lời giải:

Bài 22 trang 45 sách bài tập Toán 7: Tính giá trị của mỗi biểu thức:

a) $| - 11 | + | 22 | + | - 33 | - 44$ ;

b) $2. | - 21 | - 3. | 125 | - 5. | - 33 | - | 2.21 |$ ;

c) $2, 8 + 3. | - \frac{13}{3} | + 0, 2. | 6 | + 5. | - 10 |$ ;

d) $(- 1, 5) + 2. | 2 \frac{1}{2} | - 6. | \frac{- 16}{3} | + 5. | - 0, 3 |$ .

Lời giải:

$\begin{array}{l} | - 11 | + | 22 | + | - 33 | - 44 \\ = - (- 11) + 22 + - (- 33) - 44 \\ = 11 + 22 + 33 - 44 \\ = 66 - 44 = 22 \end{array}$

$\begin{array}{l} 2. | - 21 | - 3. | 125 | - 5. | - 33 | - | 2.21 | \\ = 2. 21 - 3.125 - 5. 33 - 42 \\ = 42 - 375 - 165 - 42 = - 540 \end{array}$

$\begin{array}{l} 2, 8 + 3. | - \frac{13}{3} | + 0, 2. | 6 | + 5. | - 10 | \\ = 2, 8 + 3. \frac{13}{3} + 0, 2.6 + 5. 10 \\ = 2, 8 + 13 + 1, 2 + 50 \\ = (2, 8 + 1, 2) + (13 + 50) \\ = 4 + 63 = 67 \end{array}$

$\begin{array}{l} (- 1, 5) + 2. | 2 \frac{1}{2} | - 6. | \frac{- 16}{3} | + 5. | - 0, 3 | \\ = (- 1, 5) + 2. \frac{5}{2} - 6. \frac{- 16}{3} + 5. 0, 3 \\ = (- 1, 5) + 5 - 32 + 1, 5 \\ = [(- 1, 5) + 1, 5] + (5 - 32) \\ = 0 + (- 27) = - 27 \end{array}$

Bài 23 trang 45 sách bài tập Toán 7: Trong giờ hoạt động của câu lạc bộ Toán, bạn Nam phát biểu “Giá trị tuyệt đối của tổng hai số thực khác dấu bất kì luôn là một số dương”. Bạn Nam phát biểu đúng hay sai? Vì sao?

Lời giải:

Bạn Nam phát biểu sai. Vì giá trị tuyệt đối của tổng hai số thực đối nhau luôn bằng 0.

Ví dụ: $| 1 + (- 1) | = | 0 | = 0$ .

Chú ý: Ta chỉ có thể kết luận Giá trị tuyệt đối của tổng hai số thực khác dấu bất kì luôn là một số không âm.

Bài 24 trang 45 sách bài tập Toán 7: Chọn dấu “<”, “>”, “=” thích hợp cho ?:

Lời giải:

a) $| - 12 | > | 0 |$ ;

b) $| \frac{- 321}{491} | = | \frac{321}{491} |$ ;

c) $| 5, 706 | < | - 7, 01 |$ ;

d) $| - \sqrt{131} | < 131$ .

Bài 25 trang 45 sách bài tập Toán 7: Tìm số thực x, biết:

a) $| x | = \frac{13}{17}$ ;

b) $| x + 2, 037 | = 0$ ;

c) $| x - 22 | = - \sqrt{3}$ ;

d) $| x | = x$ ;

e*) $| x | + | x + 1 | = 0$ .

Lời giải:

a) $| x | = \frac{13}{17} \to x = [\begin{array}{l} x = \frac{13}{17} \\ x = - \frac{13}{17} \end{array}$ ;

b) $\begin{array}{l} | x + 2, 037 | = 0 \to x + 2, 037 = 0 \\ \to x = 0 - 2, 037 = - 2, 037 \end{array}$ ;

c) $| x - 22 | = - \sqrt{3}$ . Vì $| x - 22 | \geq 0$ mà $- \sqrt{3} < 0$ nên không tồn tại giá trị nào của x thỏa mãn $| x - 22 | = - \sqrt{3}$ .

d) $| x | = x$ với mọi số thực x không âm. Vậy $x \geq 0$ .

e*) $| x | + | x + 1 | = 0$ .

Ta có: ${\begin{cases} | x | \geq 0 \\ | x + 1 | \geq 0 \end{cases}$ nên để $| x | + | x + 1 | = 0$ thì ${\begin{cases} | x | = 0 \to x = 0 \\ | x + 1 | = 0 \to x + 1 = 0 \to x = - 1 \end{cases}$ .

Điều này là vô lí. Vậy không có giá trị nào của x thỏa mãn $| x | + | x + 1 | = 0$ .

Bài 26 trang 46 sách bài tập Toán 7: Cho hai số thực a, b. Gọi . (ảnh 1) .Chứng tỏ rằng M là số dương.

Lời giải:

Ta có:

${\begin{cases} \sqrt{19} > 0 \\ | a | > 0 \\ b^{2} > 0 \\ (a - b)^{2} > 0 \end{cases}$ với mọi số thực a, b thỏa mãn $(a \neq 0, b \neq 0, a \neq b)$ .

Vậy $\sqrt{19} . | a | . b^{2} . (a - b)^{2} > 0$ hay M là số dương.

Bài 27 trang 46 sách bài tập Toán 7: Cho 100 số thực, trong đó tích của ba số bất kì là một số âm. Chứng tỏ rằng tích của 100 số thực đó là một số dương.

Lời giải:

Tích của ba số thực bất kì là một số âm, suy ra trong 3 số đó có ít nhất 1 số là số âm.

Gọi số âm đó là x.

Trừ số âm x ra thì ta còn 99 số còn lại được chia thành 33 nhóm, mỗi nhóm 3 số.

Mà tích của 3 số bất kì là một số âm nên tích của 33 nhóm cũng là một số âm.

Suy ra: tích của 100 số thực bằng tích của số âm x nhân với tích của 33 nhóm số cũng là một số âm.

Vậy tích của 100 số thực là một số dương.

Bài 28 trang 46 sách bài tập Toán 7:

(ảnh 1)

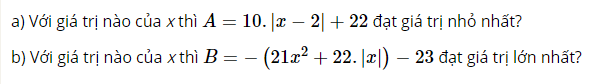
Lời giải:

a) Ta có: $| x - 2 | \geq 0 \to 10. | x - 2 | + 22 \geq 10.0 + 22 = 22$ .

Suy ra giá trị nhỏ nhất của A là 22.

Vậy $A = 22 \Leftrightarrow | x - 2 | = 0 \Leftrightarrow x - 2 = 0 \Leftrightarrow x = 2$ .

b) Ta có: $\begin{array}{l} {\begin{cases} 21 x^{2} \geq 0 \\ | x | \geq 0 \end{cases} \to 21 x^{2} + 22. x \geq 0 \\ \Rightarrow - (21 x^{2} + 22. x) \leq 0 \end{array}$