Toptailieu.vn giới thiệu Giải bài tập Toán lớp 7 Bài 3: Tam giác cân sách Chân trời sáng tạo giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 7 Tập 2. Mời các bạn đón xem:

Giải Toán lớp 7 trang 59, 60, 61, 62, 63 Bài 3: Tam giác cân

Câu hỏi mở đầu trang 59 Toán lớp 7: Em hãy đo rồi so sánh độ dài hai cạnh AB và AC của tam giác ABC có trong hình di tích ga xe lửa Đà Lạt dưới đây.

Phương pháp giải 

Đo và so sánh độ dài các cạnh trong tam giác ABC

Lời giải 

Ta thấy độ dài của 2 cạnh AB = AC

1. Mục 1

Hoạt động 1 trang 59, 60 Toán lớp 7: Gấp đôi một tờ giấy hình chữ nhật ABCD theo đường gấp MS. Cắt hình gấp được theo đường chép AS rồi trải phẳng hình cắt được ra ta có tam giác SAB (Hình 1). Em hãy so sánh hai cạnh SA và SB của tam giác này.

Phương pháp giải:

Gập giấy và cắt như hướng dẫn

Lời giải 

Ta thấy sau khi cắt 2 cạnh của tam giác bằng nhau

Thực hành 1 trang 59, 60 Toán lớp 7: Tìm các tam giác cân trong Hình 4. Kể tên các cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của mỗi tam giác cân đó.

Phương pháp giải:

Dựa vào số đo các cạnh của tam giác để tìm tam giác cân

Lời giải 

Ta thấy: $\mathrm{\Delta }MEF$cân tại M do ME = MF có:

+ cạnh bên: ME, MF

                        + cạnh đáy: EF

+ góc ở đỉnh: $\widehat{EMF}$

                        + góc ở đáy: $\widehat{MEF}$,$\widehat{MFE}$

  $\mathrm{\Delta }MNP$ cân tại M do MN = MP có:

            + cạnh bên: MN, MP

            + cạnh đáy: NP

            + góc ở đỉnh: $\widehat{NMP}$

            + góc ở đáy: $\widehat{NPM}$, $\widehat{PNM}$

  $\mathrm{\Delta }MHP$ cân tại M do MH = MP có:

            + cạnh bên : MH, MP

            + cạnh đáy: HP

            + góc ở đỉnh: $\widehat{PMH}$

            + góc ở đáy: $\widehat{MPH}$,$\widehat{MHP}$

2. Mục 2

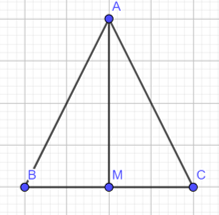
Hoạt động 2 trang 60, 61, 62 Toán lớp 7: Cho tam giác ABC cân tại A (Hình 5). Gọi M là trung điểm cạnh BC. Nối A với M. Em hãy làm theo gợi ý sau để chứng minh $\widehat{ABC}$=$\widehat{ACB}$.

Xét $\mathrm{\Delta }AMB$ và $\mathrm{\Delta }AMC$có:

AB = ? (?)

MB = MC (?)

AM là cạnh ?

Vậy $\mathrm{\Delta }AMB$ =$\mathrm{\Delta }AMC$ (c.c.c)

Suy ra $\widehat{ABC}$=$\widehat{ACB}$

Phương pháp giải:

Dựa vào định nghĩa của tam giác cân là tam giác có 2 cạnh bằng nhau

Lời giải 

Xét $\mathrm{\Delta }AMB$ và $\mathrm{\Delta }AMC$.có:

AB = AC ( do tam giác ABC cân tại A )

MB = MC ( do M là trung điểm BC )

AM là cạnh chung

=>$\mathrm{\Delta }AMB$ =$\mathrm{\Delta }AMC$ (c.c.c)

=>$\widehat{ABC}$=$\widehat{ACB}$( 2 góc tương ứng)

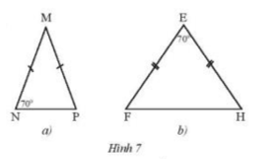
Thực hành 2 trang 60, 61, 62 Toán lớp 7: Tìm số đo các góc chưa biết của mỗi tam giác trong Hình 7.

Phương pháp giải:

Dựa vào định lí 2 góc đáy của tam giác cân bằng nhau

Lời giải 

a) Vì $\mathrm{\Delta }MNP$ cân tại M ( theo giả thiết )

$\Rightarrow \hat{N}=\hat{P}={70}^o$ ( 2 góc đáy của tam giác cân )

$\Rightarrow \hat{M}={180}^o-{2.70}^o={40}^o$

b) Xét $\mathrm{\Delta }EFH$ cân tại E

Theo định lí về tổng 3 góc trong tam giác ta có

$\Rightarrow \hat{E}+\hat{F}+\hat{H}={180}^o$

Mà $\hat{F}=\hat{H}$( tính chất tam giác cân )

$\Rightarrow \hat{F}=\hat{H}={180}^o-\hat{E}=({180}^o-{70}^o):2={55}^o$ 

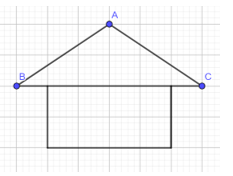
Vận dụng 1 trang 60, 61, 62 Toán lớp 7: Trong hình mái nhà ở Hình 8, tính góc B và góc C, biết $\hat{A}$= ${110}^o$.

Phương pháp giải:

Dựa vào tính chất 2 góc đáy của tam giác cân bằng nhau

Lời giải

Vì tổng số đo 3 góc trong tam giác là ${180}^o$

$\Rightarrow \hat{A}+\hat{B}+\hat{C}={180}^o$

Mà $\hat{B}=\hat{C}$$=({180}^o-\hat{A}):2$$=({180}^o-{110}^o):2={35}^o$ 

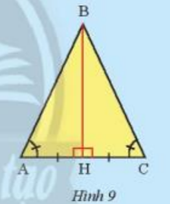
Hoạt động 3 trang 60, 61, 62 Toán lớp 7: Cho tam giác ABC có $\hat{A}$=$\hat{C}$. Vẽ đường thẳng đi qua điểm B, vuông góc với AC và cắt AC tại điểm H (Hình 9). Em hãy làm theo gợi ý sau để chứng minh BA = BC.

Xét $\mathrm{\Delta }AHB$và $\mathrm{\Delta }CHB$cùng vuông tại H, ta có:

BH là cạnh góc vuông ?

$\widehat{HAB}$ = $\widehat{HCB}$ suy ra $\widehat{ABH}=\widehat{CBH}$ (?)

Vậy $\mathrm{\Delta }AHB=\mathrm{\Delta }CHB$. Suy ra BA = BC

Phương pháp giải:

Ta chứng minh $\mathrm{\Delta }AHB=\mathrm{\Delta }CHB$ rồi từ đó suy ra BA = BC 

Lời giải

Xét $\mathrm{\Delta }AHB$ và $\mathrm{\Delta }CHB$ cùng vuông tại H, ta có:

BH là cạnh góc vuông của và

$\widehat{ABH}=\widehat{CBH}$( Do cùng bằng ${90}^o-\widehat{HAB}={90}^o-\widehat{HCB}$ )

$\Rightarrow$ $\mathrm{\Delta }AHB=\mathrm{\Delta }CHB$

$\Rightarrow$ BA = BC

Thực hành 3 trang 60, 61, 62 Toán lớp 7: Tìm các tam giác cân trong Hình 11 và đánh dấu vào các cạnh bằng nhau.

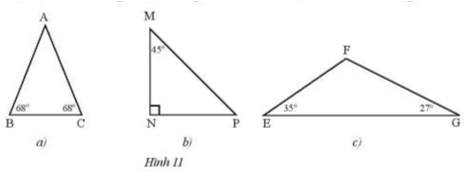
Phương pháp giải:

Ta tìm các tam giác cân từ các góc ở đáy rồi suy ra các cạnh bằng nhau

Lời giải 

a) Ta có tam giác ABC cân tại A do 2 góc đáy B, C cùng bằng 68°

Nên AB = AC

b) Vì tổng các góc trong tam giác = 180° nên $\hat{M}+\hat{N}+\hat{P}={180}^o$

$\Rightarrow \hat{P}={180}^o-{45}^o-{90}^o={45}^o$

$\Rightarrow$ $\mathrm{\Delta }MNP$ vuông cân tại N

$\Rightarrow$ MN = NP

c) Xét $\mathrm{\Delta }EFG$ theo định lí về tổng số đo các góc trong tam giác ta có :

$\Rightarrow \hat{F}+\hat{E}+\hat{G}={180}^o$

$\Rightarrow \hat{F}={180}^o-{35}^o-{27}^o={118}^o$

$\Rightarrow \mathrm{\Delta }EFG$ không cân nên không có các cặp cạnh bằng nhau  

Vận dụng 2 trang 60, 61, 62 Toán lớp 7: Cho tam giác ABC cân tại A có góc B bằng ${60}^o$. Chứng minh rằng tam giác ABC đều.

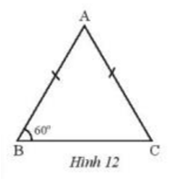
Phương pháp giải:

Ta chứng minh 3 góc của tam giác đều bằng ${60}^o$

Lời giải 

Ta có: tam giác ABC cân tại A

Nên $\hat{B}=\hat{C}={60}^o$( 2 góc đáy của tam giác cân )

Theo định lí về tổng 3 góc trong tam giác ta có : $\hat{A}+\hat{B}+\hat{C}={180}^o$

$\Rightarrow \hat{A}={180}^o-{60}^o-{60}^o={60}^o$

Vì $\hat{A}=\hat{B}=\hat{C}={60}^o$$\Rightarrow$ tam giác ABC là tam giác đều

3. Bài tập

Bài 1 trang 62 Toán lớp 7: Tìm các tam giác cân và tam giác đều trong mỗi hình sau (Hình 13). Giải thích.

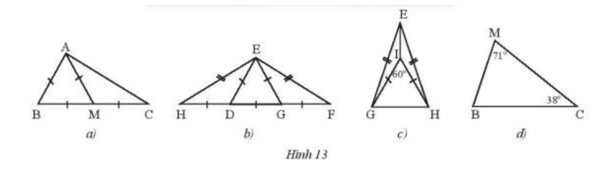
Phương pháp giải 

- Dựa vào các cạnh bên và số đo các góc ở đáy mỗi tam giác

Lời giải

a) Tam giác ABM là tam giác đều do có 3 cạnh bằng nhau

Tam giác AMC cân tại M do AM = MC

b) Tam giác EDG là tam giác đều do có 3 cạnh bằng nhau

Tam giác EHF cân tại E do EH = EF

Tam giác EDH cân tại D do DH = DE

c) Tam giác EGF cân tại G do GE = GF

Tam giác IHG đều do là tam giác cân có 1 góc = 60°

Tam giác EHG cân tại E do EG = EH

d) Tam giác MBC không cân và không đều vì 3 góc có số đo khác nhau

Bài 2 trang 62 Toán lớp 7: Cho Hình 14, biết ED = EF và EI là tia phân giác của $\stackrel{⏜}{DEF}$

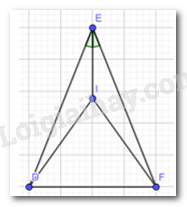
Chứng minh rằng:

a)ΔEID=ΔEIF

b) Tam giác DIF cân

Phương pháp giải 

- Ta sử dụng tính chất c-g-c để chứng minh câu a

- Từ câu a ta suy ra ID = FI và chứng minh được tam giác DIF cân

Lời giải 

a) Xét tam giác EID và tam giác EIF có :

IE chung

ED = EF

$\widehat{IED}=\widehat{IEF}$( EI là tia phân giác của $\widehat{DEF}$)

$\Rightarrow \mathrm{\Delta }EID=\mathrm{\Delta }EIF(c-g-c)$

b) Vì $\mathrm{\Delta }EID=\mathrm{\Delta }EIF$ nên ID = IF ( 2 cạnh tương ứng )

Do đó tam giác DIF cân tại I (theo định nghĩa tam giác cân)

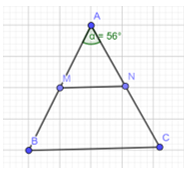
Bài 3 trang 63 Toán lớp 7: Cho tam giác ABC cân tại A có $\stackrel{⏜}{A}=56°$(Hình 15)

a) Tính $\stackrel{⏜}{B}, \stackrel{⏜}{C}$

b) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng tam giác AMN cân.

c) Chứng minh rằng MN // BC

Lời giải

a) Theo đề bài ta có tam giác ABC cân ở A và $\hat{A}={56}^o$

Mà $\Rightarrow \hat{A}+\hat{B}+\hat{C}={180}^o$

$\Rightarrow \hat{B}=\hat{C}=({180}^o-{56}^o):2={62}^o$

b) Vì tam giác ABC cân tại A nên AB = AC ( định nghĩa tam giác cân )

Mà M, N là trung điểm của AB, AC

Nên AM = AN

Xét tam giác AMN có AM = AN nên AMN là tam giác cân tại A

$\Rightarrow \hat{M}=\hat{N}=({180}^o-{56}^o):2={62}^o$

c) Vì $\widehat{AMN}=\widehat{ABC}$ (cùng bằng 62°)

Mà chúng ở vị trí đồng vị nên MN⫽BC

Bài 4 trang 63 Toán lớp 7: Cho tam giác ABC cân tại A (Hình 16). Tia phân giác của góc B cắt AC tại F, tia phân giác của góc C cắt AB tại E.

a) Chứng minh rẳng $\widehat{ABF}=\widehat{ACE}$

b) Chứng minh rằng tam giác AEF cân

c) Gọi I là giao điểm của BF và CE. Chứng minh rằng tam giác IBC và tam giác IEF là những tam giác cân

Lời giải

a) Vì tam giác ABC cân tại A

$\Rightarrow \hat{B}=\hat{C}\Rightarrow {\displaystyle \frac{1}{2}}\hat{B}={\displaystyle \frac{1}{2}}\hat{C}\Rightarrow \widehat{ABF}=\widehat{ACE}$

b) Xét $\mathrm{\Delta }ECA$ và $\mathrm{\Delta }FBA$có:

$\hat{A}$ chung

AB = AC

$\widehat{ABF}=\widehat{ACE}$

$\Rightarrow$$\mathrm{\Delta }ECA$= $\mathrm{\Delta }FBA$( g – c – g )

$\Rightarrow AE=AFvàEC=BF$ (2 cạnh tương ứng)

$\Rightarrow \mathrm{\Delta }AEF$ cân tại A

c) Xét tam giác IBC có :

$\hat{B}=\hat{C}\Rightarrow {\displaystyle \frac{1}{2}}\hat{B}={\displaystyle \frac{1}{2}}\hat{C}\Rightarrow \widehat{ICB}=\widehat{IBC}$

Do đó, tam giác IBC cân tại I ( 2 góc ở đáy bằng nhau )

$\Rightarrow IB=IC$( cạnh tương ứng )

Vì EC = BF ( câu b) và IB = IC

$\Rightarrow$ EC – IC = BF – BI

$\Rightarrow$ EI = FI

$\Rightarrow \mathrm{\Delta }IEF$ cân tại I

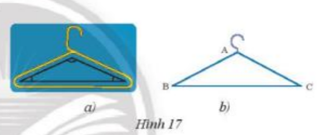
Bài 5 trang 63 Toán lớp 7: Phần thân của một móc treo quần áo có dạng hình tam giác cân (Hình 17a) được vẽ lại như Hình 17b. Cho biết AB = 20 cm; BC = 28 cm và $\stackrel{⏜}{B}=35°$. Tìm số đo các góc còn lại và chu vi của tam giác ABC.

Lời giải 

Vì tam giác ABC cân tại A

$\Rightarrow$ AB = AC ( định lí tam giác cân ) = 20 cm

$\Rightarrow$ Chu vi tam giác ABC = AB + AC + BC = 20 + 20 + 28 = 68 cm

Vì ABC là tam giác cân tại A $\Rightarrow \hat{B}=\hat{C}$ ( 2 góc ở đáy ) = 35°

Mà theo định lí tổng 3 góc trong tam giác = 180°

$\Rightarrow \hat{A}={180}^o-\hat{B}-\hat{C}={180}^o-{35}^o-{35}^o={110}^o$

Bài 6 trang 63 Toán lớp 7: Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.

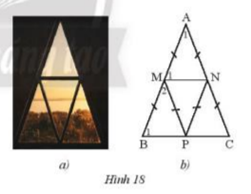
a) Cho biết $\widehat{A_1}$$={42}^o$. Tính số đo của $\widehat{M_1}$,$\widehat{B_1}$,$\widehat{M_2}$.

b) Chứng minh MN // BC, MP // AC.

c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.

Phương pháp giải 

Sử dụng các tính chất của tam giác cân

Lời giải 

a) Ta thấy tam giác AMN cân tại A do AM = AN

$\stackrel{⏜}{M_1}=(180°-\stackrel{⏜}{A_1}):2=(180°-42°):2=69°$

Ta thấy tam giác PMN = tam giác AMN ( c-c-c )

$\Rightarrow \widehat{M_1}=\widehat{PMN}={69}^o$ (góc tương ứng )

Mà $\Rightarrow \widehat{M_1}+\widehat{M_2}+\widehat{PMN}={180}^o$( các góc kề bù )

$\Rightarrow \widehat{M_2}={180}^o-{69}^o-{69}^o={42}^o$

Mà tam giác MPB cân tại M do MB = MP nên

$\Rightarrow \widehat{B_1}=\widehat{MPB}$

Áp dụng định lí tổng 3 góc trong tam giác

$\Rightarrow \widehat{B_1}=({180}^o-{42}^o):2={69}^o$

b)      Ta thấy $\widehat{B_1}$và $\widehat{M_1}$ở vị trí đồng vị và bằng nhau nên

$\Rightarrow$MN⫽BC

Vì tam giác PMN = tam giác AMN nên ta có

$\Rightarrow \widehat{M_1}=\widehat{ANM}=\widehat{PMN}=\widehat{MNP}$( do 2 tam giác cân và bằng nhau )

Mà $\widehat{MNA}$và$\widehat{PMN}$ ở vị trí so le trong

$\Rightarrow$MP⫽AC

c)      Ta có $\mathrm{\Delta }AMN=\mathrm{\Delta }PMN=\mathrm{\Delta }MBP(c-g-c)$(1)

Vì MP⫽AC ( chứng minh trên )

$\Rightarrow \widehat{MPN}=\widehat{PNC}$ ( 2 góc so le trong ) =${42}^o$

$\Rightarrow \mathrm{\Delta }MPN=\mathrm{\Delta }NCP(c-g-c)$(2)

Từ (1) và (2) $\Rightarrow$ 4 tam giác cân AMN, MBP, PMN, NCP bằng nhau