Với giải Bài 1 trang 66 Chuyên đề Toán 10 Cánh diều chi tiết trong Bài 8: Ba đường conic giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Chuyên đề Toán 10. Mời các bạn đón xem:

Giải bài tập Chuyên đề Toán lớp 10 Bài 8: Ba đường conic

Bài 1 trang 66 Chuyên đề Toán 10: Cho hình chữ nhật ABCD với bốn đỉnh A(–4; 3), B(4; 3), C(4; –3), D(–4; –3).

a) Viết phương trình chính tắc của elip nhận ABCD là hình chữ nhật cơ sở. Vẽ elip đó.

b) Viết phương trình chính tắc của hypebol nhận ABCD là hình chữ nhật cơ sở. Vẽ hypebol đó.

Lời giải:

Gọi M, N lần lượt là trung điểm của AB, BC.

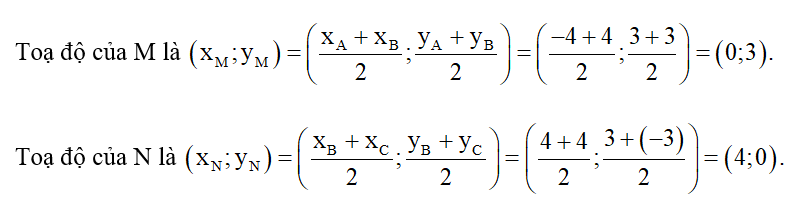
a) Gọi phương trình chính tắc của elip cần tìm là $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ (a > b > 0).

Vì ABCD là hình chữ nhật cơ sở của elip nên M, N là hai đỉnh của elip.

Lại có: M(0; 3) $\Rightarrow$ b = 3, N(4; 0)$\Rightarrow$ a = 4.

Vậy phương trình chính tắc của elip cần tìm là$\frac{x^2}{16}+\frac{y^2}{9}=1.$

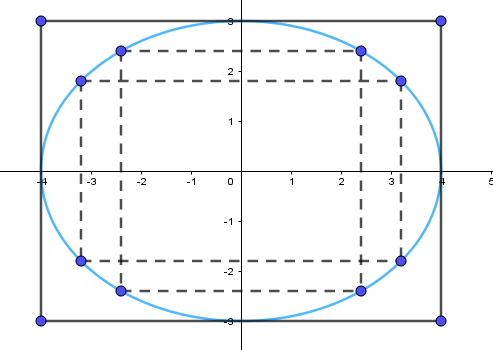
+) Vẽ elip:

Ta thấy a = 4, b = 3. Toạ độ các đỉnh của elip là (–4; 0), (5; 0), (0; – 3), (0; 3).

Bước 1. Vẽ hình chữ nhật cơ sở có bốn cạnh thuộc bốn đường thẳng x = –4, x = 4, y = –3, y = 3.

Bước 2. Tìm một số điểm cụ thể thuộc elip, chẳng hạn ta thấy điểm $X\left(\frac{12}{5};\frac{12}{5}\right)$ và điểm $Y\left(\frac{16}{5};\frac{9}{5}\right)$ thuộc (E). Do đó các điểm

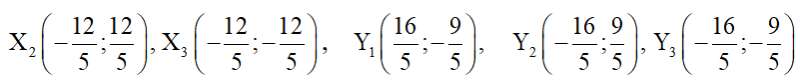
cũng thuộc (E)

Bước 3. Vẽ đường elip (E) đi qua các điểm cụ thể trên, nằm ở phía trong hình chữ nhật cơ sở và tiếp xúc với các cạnh của hình chữ nhật cơ sở tại bốn đỉnh của (E) là
(–4; 0), (4; 0), (0; –3), (0; 3).

b)

Gọi phương trình chính tắc của hypebol cần tìm là $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$ (a > 0, b > 0).

Vì M(0; 3) và N(4;0) là trung điểm các cạnh của hình chữ nhật cơ sở nên a = 4, b = 3.

Vậy phương trình chính tắc của hypebol cần tìm là $\frac{x^2}{16}-\frac{y^2}{9}=1.$

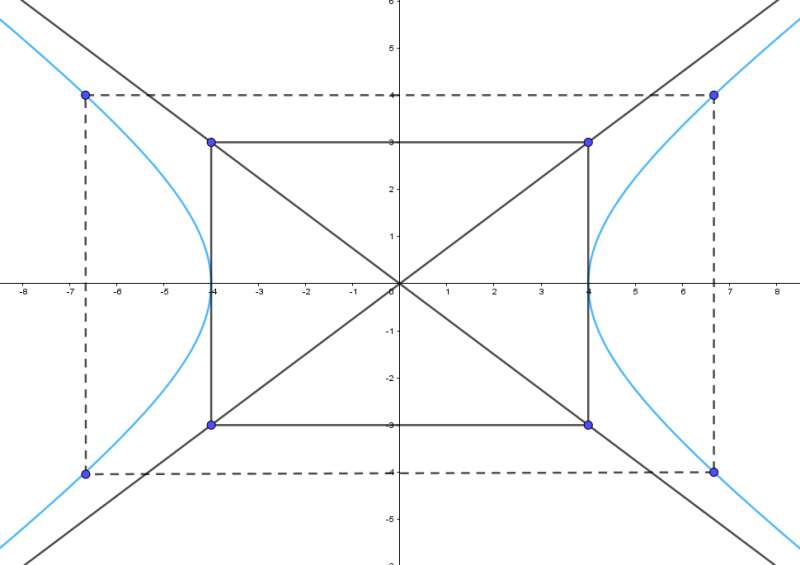
+) Vẽ hypebol:

Ta thấy a = 4, b = 3. (H) có các đỉnh là (–4; 0), (4; 0).

Bước 1. Vẽ hình chữ nhật cơ sở có bốn cạnh thuộc bốn đường thẳng x = –4, x = 4, y = –3, y = 3.

Bước 2. Vẽ hai đường chéo của hình chữ nhật cơ sở.

Tim một số điểm cụ thể thuộc hypebol, chẳng hạn ta thấy điểm $X\left(\frac{20}{3};4\right)$ thuộc (H). Do đó các điểm $X_1\left(\frac{20}{3};-4\right),X_2\left(-\frac{20}{3};4\right),X_3\left(-\frac{20}{3};-4\right)$ thuộc (H).

Bước 3. Vẽ đường hypebol bên ngoài hình chữ nhật cơ sở; nhánh bên trái tiếp xúc với cạnh của hình chữ nhật cơ sở tại điểm (–4; 0) và đi qua X₂, X₃; nhánh bên phải tiếp xúc với cạnh của hình chữ nhật cơ sở tại điểm (4; 0) và đi qua X, X₁. Vẽ các điểm thuộc hypebol càng xa gốc toạ độ thì càng sát với đường tiệm cận. Hypebol nhận gốc toạ độ là tâm đối xứng và hai trục toạ độ là hai trục đối xứng.

Xem thêm lời giải bài tập Chuyên đề học tập Toán 10 Cánh diều hay, chi tiết khác:

Hoạt động trang 60 Chuyên đề Toán 10:Quan sát Hình 22a, Hình 22b, Hình 22c và nêu tỉ số khoảng cách từ một điểm M nằm trên mỗi đường conic đến tiêu điểm của nó và khoảng cách từ điểm M đến đường chuẩn ....

• Bài 2 trang 67 Chuyên đề Toán 10: Các đường conic có phương trình như sau là đường elip hay hypebol? Tìm độ dài các trục, toạ độ tiêu điểm, tiêu cự, tâm sai của các đường conic đó. a) x²/100 + y²/64 = 1 ; ....

• Bài 3 trang 67 Chuyên đề Toán 10: Cho parabol có phương trình chính tắc y² = 2x. Tìm tiêu điểm, phương trình đường chuẩn của parabol và vẽ parabol đó ....

• Bài 4 trang 67 Chuyên đề Toán 10: Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ: x = –5 và điểm F(–4; 0). Cho ba điểm A(–3; 1), B(2; 8), C(0; 3) ....

• Bài 5 trang 67 Chuyên đề Toán 10: Vệ tinh nhân tạo đầu tiên được Liên Xô (cũ) phóng từ Trái Đất năm 1957. Quỹ đạo của vệ tinh đó là một đường elip nhận tâm Trái Đất là một tiêu điểm. Người ta đo được vệ tinh cách bề mặt Trái Đất gần nhất là 583 dặm và xa nhất là 1342 dặm (1 dặm xấp xỉ 1,609 km) ....

• Bài 6 trang 67 Chuyên đề Toán 10: Sao Diêm Vương chuyển động xung quanh Mặt Trời theo quỹ đạo là một đường elip có một trong hai tiêu điểm là tâm của Mặt Trời. Biết elip này có bán trục lớn a ≈ 5,906 . 106 km và tâm sai e ≈ 0,249 ....

• Bài 7 trang 67 Chuyên đề Toán 10: Cho đường thẳng Δ và điểm O sao cho khoảng cách từ O đến Δ là OH = 1 (Hình 39). Với mỗi điểm M di động trong mặt phẳng, gọi K là hình chiếu vuông góc của M lên Δ. Chứng minh tập hợp các điểm M trong mặt phẳng sao cho MK² – MO² = 1 ....

•