Với giải Câu hỏi trang 24 Toán 10 Tập 2 Chân trời sáng tạo trong Bài 1: Quy tắc cộng và quy tắc nhân giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Chân trời sáng tạo trang 24 Bài 1: Quy tắc cộng và quy tắc nhân
a) Khách hàng có bao nhiêu lựa chọn về màu ngoại thất và nội thất khi mua một chiếc xe ô tô mẫu này?
b) Hãy vẽ sơ đồ hình cây để giải thích cho kết quả tính toán ở trên.
Lời giải
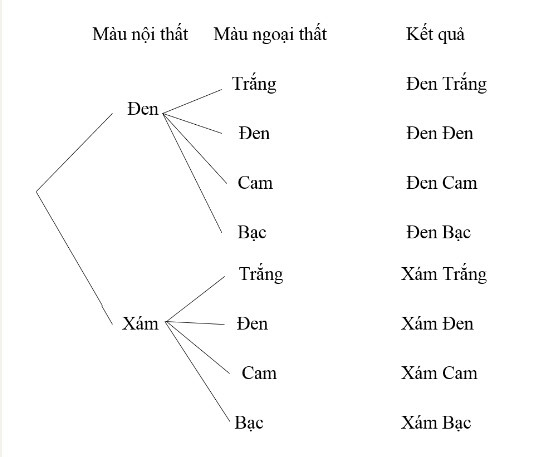
a) Việc chọn màu nội thất và ngoại thất của mẫu o tô này gồm 2 công đoạn:
Công đoạn thứ nhất: Chọn màu nội thất, có 2 cách chọn: đen hoặc xám
Công đoạn thứ hai: Chọn màu ngoại thất, có 4 cách chọn: trắng, đen, cam hoặc bạc
Theo quy tắc nhân, có cách chọn màu nội thất và ngoại thất của một chiếc ô tô mẫu này
b) Sơ đồ hình cây có dạng như sau
a) Không có nucleotide A nào?
b) Có nucleotide A nằm ở vị trí đầu tiên?
Phương pháp giải:
Bước 1: Xác định cách chọn từng nucleotide
Bước 2: Áp dụng quy tắc nhân
Lời giải
a) Có thể tạo nên một đoạn phân tử RNA có 4 phân tử nucleotide là một công việc gồm 4 công đoạn, mỗi công đoạn ứng với việc chọn một trong ba loại nucleotide C, G hoặc U cho mỗi vị trí (thứ nhất, thứ hai, thứ ba và cuối cùng) của đoạn. Như vậy, mỗi công đoạn có 3 cách thực hiện. Theo quy tắc nhân, 4 công đoạn có số cách thực hiện là
Vậy có nhiều nhất đoạn phân tử RNA khác nhua cùng có 4 phân tử nucleotide và không có nucleotide A
b)
Có thể tạo nên một đoạn phân tử RNA có 4 phân tử nucleotide là một công việc gồm 4 công đoạn, mỗi công đoạn ứng với việc chọn một trong ba loại nucleotide C, G hoặc U cho mỗi vị trí (thứ nhất, thứ hai, thứ ba và cuối cùng) của đoạn.
Công đoạn thứ nhất: Chọn nucleotide A ở vị trí đầu tiên, có 1 cách chọn
Công đoạn thứ hai: Chọn một trong bốn loại nucleotide A, C, G hoặc U cho mỗi vị trí (thứ hai, thứ 3 và vị trí cuối) của đoạn. Như vậy mỗi công đoạn sau sẽ có 4 cách thực hiện.
Theo quy tắc nhân, 4 công đoạn thực hiện có số cách là
Vậy có nhiều nhất đoạn phân tử RNA khác nhau chứa 4 phân tử nucleotide có nucleotide A nằm ở vị trí đầu tiên.
Phương pháp giải:
Bước 1: Xác định số cách chọn của từng công đoạn (chọn chữ cái, chọn 2 chữ số sau)
Bước 2: Áp dụng quy tắc nhân
Lời giải
Để công ty kiến tạo mã số gồm 3 kí tự gồm một chữ cái tiếng anh viết hoa đứng trước hai chữ số cần thực hiện 3 công đoạn
Công đoạn 1: Chọn 1 trong 24 chữ cái tiếng anh viết hoa đứng đầu, có 24 cách chọn
Công đoạn 2: Chọn 1 chữ số trong 10 chữ số cho hai vị trí số sau chữ cái kia, có 10 cách chọn
Theo quy tắc nhân, 3 công đoạn thực hiện có số cách là
Suy ra có 2400 mã số nhân viên được tạo ra theo yêu cầu của mã số
Vậy số mã số theo công ty đề ra không đủ để cấp cho nhân viên (mỗi người một mã) nếu công ty đó có 2500 nhân viên.
Bài tập
a) có bao nhiêu cách chọn một quả dưa hấu hoặc một quả thanh long.
b) có bao nhiêu cách chọn một quả dưa hấu và 1 quả thanh long.

Phương pháp giải
Bước 1: Xác định cách chọn từng loại quả
Bước 2:
a) Áp dụng quy tắc cộng
b) Áp dụng quy tắc nhân
Lời giải
a) Việc chọn một quả dưa hấu hoặc một quả thanh long được thực hiện qua 2 phương án
Phương án 1: Chọn một quả dưa hấu, có 6 cách thực hiện
Phương án 2: Chọn một quả thanh long, có 15 cách thực hiện
Áp dụng quy tắc cộng, số cách chọn một quả dưa hấu hoặc một quả thanh long là
(cách chọn)
b) Việc chọn một quả dưa hấu và một quả thanh long được thực hiện qua 2 công đoạn:
Công đoạn 1: Chọn một quả dưa hấu, có 6 cách thực hiện
Công đoạn 2: Chọn một quả thanh long, có 15 cách thực hiện
Áp dụng quy tắc nhân, số cách chọn một quả thanh long và một quả dưa hấu là
(cách chọn)
a) Tính số kết quả có thể xảy ra
b) Vẽ sơ đồ hình cây và liệt kê tất cả cả các kết quả đó.

Phương pháp giải
a) Bước 1: Xác định số kết quả xuất hiện trên đồng xu và xúc xắc
Bước 2: Áp dụng quy tắc nhân
Lời giải
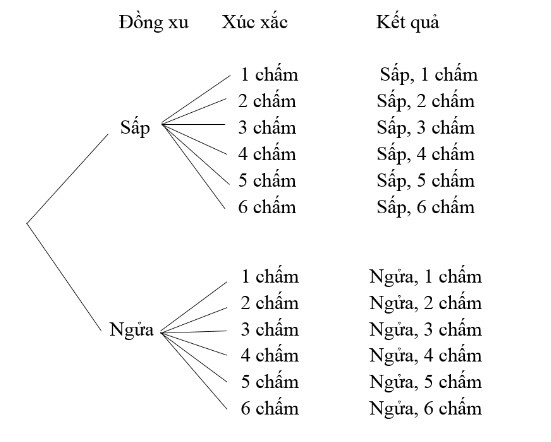
a) Kết quả của đồng xu và xúc xắc xảy ra đồng thời nên kết quả xảy ra gồm 2 kết quả liên tiếp nhau
Kết quả 1: Kết quả của đồng xu, có 2 kết quả: Sấp và ngửa
Kết quả 2: Kết quả của xúc xắc, có 6 kết quả: mỗi kết quả của mỗi mặt con xúc xắc
Áp dụng quy tắc nhân, ta có số kết quả có thẻ xuất hiện khi gieo đồng thời một đồng xu và một con xúc xắc là:
Vậy có 12 kết quả có thể xáy ra
b)
Phương pháp giải
Bước 1: Xác định số cách chọn mỗi loại thức ăn và đồ uống (món chính, món phụ và đồ uống)
Bước 2: Áp dụng quy tắc nhân.
Lời giải
Việc thực hiện bữa trưa gồm một món chính, một món phụ và một loại đồ uống gồm 3 công đoạn
Công đoạn 1: Chọn 1 món chính trong 5 món, có 5 cách chọn
Công đoạn 2: Chọn 1 món phụ trong 3 món, có 3 cách chọn
Công đoạn 3: Chọn 1 loại đồ uống trong 4 loại, có 4 cách chọn
Áp dụng quy tắc nhân, ta có số cách chọn một bữa trưa đầy đủ là
Vậy có 60 cách chọn bữa trưa gồm một món chính, một món phụ và một loại đồ uống.
Phương pháp giải
Bước 1: Xác định số cách chọn của các vị trí (chữ số hàng trăm, hàng chục, hàng đơn vị)
Bước 2: Áp dụng quy tắc nhân
Lời giải
Giả sử chữ số cần tìm có dạng
Chữ số a là chữ số hàng trăm và là chữ số chẵn nên có 4 cách chọn (2, 4, 6, 8)
Chữ số c là chữ số hàng số hàng đơn vị và là chữ số lẻ nên có 5 cách chọn (1, 3, 5, 7, 9)
Chữ số b không có điều kiện ràng buộc nên có 10 cách chọn từ 10 chữ số bất kì
Áp dụng quy tắc nhân, ta có số số tự nhiên thỏa mãn yêu cầu là:
Vậy có 200 số tự nhiên có 3 chữ số, trong đó chữ số hàng trăm là chữ số chẵn, chữ số hàng đơn vị là chữ số lẻ.
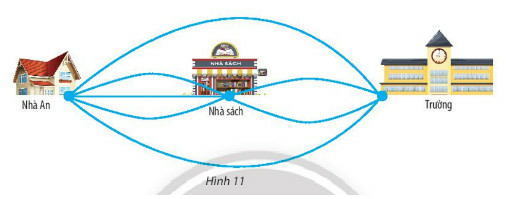
a) An có bao nhiêu cách đi từ nhà đến trường mà có đi qua nhà sách?
b) An có bao nhiêu cách đi từ nhà đến trường?
Lưu ý: Chỉ tính những đường đi qua các điểm (nhà An, nhà sách, nhà trường) không quá 1 lần
Phương pháp giải
a) Bước 1: Xác định số cách đi từ nhà đến nhà sách, từ nhà sách đến trường
Bước 2: Áp dụng quy tắc nhân
b) Bước 1: Xác định số cách đi từ nhà đến trường qua nhà sách
Bước 2: Xác định số cách đi từ nhà đến trường không qua nhà sách
Bước 3: Áp dụng quy tắc cộng
Lời giải
a) Việc đi từ nhà đến trường qua nhà sách được thực hiện qua hai công đoạn:
Công đoạn 1: Đi từ nhà đến nhà sách, có 3 con đường
Công đoạn 2: Đi từ nhà sách đến trường, có 2 con đường
Số cách đi từ nhà đến trường qua nhà sách có số cách là:
(cách)
b) Việc đi từ nhà đến trường có 2 phương án
Phương án 1: Đi từ nhà đến trường qua nhà sách, có 6 cách thực hiện (kết quả của câu a))
Phương án 2: Đi từ nhà đến trường không qua nhà sách có 2 cách
Áp dụng quy tắc cộng, ta có số cách đi từ nhà đến trường là:
(cách).
Xem thêm các bài giải Toán 10 Chân trời sáng tạo hay, chi tiết khác:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.