Toán 10 Kết nối tri thức trang 61 Bài 10: Vecto trong mặt phẳng toạ độ

Giang Ngày: 12-02-2023 Lớp 10

405

Với giải Câu hỏi trang 61 Toán 10 Tập 1 Kết nối tri thức trong Bài 10: Vecto trong mặt phẳng toạ độ học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:

Toán 10 Kết nối tri thức trang 61 Bài 10: Vecto trong mặt phẳng toạ độ

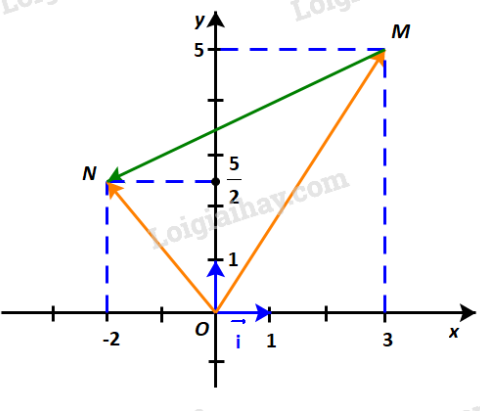
Hoạt động 2 trang 61 Toán 10: Trong Hình 4.33:

a) Hãy biểu thị mỗi vectơ $\vec{O M}, \vec{O N}$ theo các vectơ $\vec{i}, \vec{j}$ .

b) Hãy biểu thị vectơ $\vec{M N}$ theo các vectơ $\vec{O M}, \vec{O N}$ từ đó biểu thị vectơ $\vec{M N}$ theo các vectơ $\vec{i}, \vec{j}$ .

Hoạt động 2 trang 61 Toán 10 Tập 1 I Kết nối tri thức (ảnh 1)

Phương pháp giải:

a) Quy tắc hình bình hành:

Tứ giác OAMB là hình bình hành thì $\vec{O M} = \vec{O A} + \vec{O B}$

b) Quy tắc hiệu: $\vec{M N} = \vec{O N} - \vec{O M}$

Lời giải:

Dựng hình bình hành OAMB và OCND như hình dưới:

Khi đó: $\vec{O M} = \vec{O A} + \vec{O B}$ và $\vec{O N} = \vec{O C} + \vec{O D}$ .

Dễ thấy:

$\vec{O A} = 3 \vec{i}; \vec{O B} = 5 \vec{j}$ và $\vec{O C} = - 2 \vec{i}; \vec{O D} = \frac{5}{2} \vec{j}$

$\Rightarrow {\begin{cases} \vec{O M} = 3 \vec{i} + 5 \vec{j} \\ \vec{O N} = - 2 \vec{i} + \frac{5}{2} \vec{j} \end{cases}$

b) Ta có: $\vec{M N} = \vec{O N} - \vec{O M}$ (quy tắc hiệu)

$\begin{array}{l} \Rightarrow \vec{M N} = (- 2 \vec{i} + \frac{5}{2} \vec{j}) - (3 \vec{i} + 5 \vec{j}) \\ \Leftrightarrow \vec{M N} = (- 2 \vec{i} - 3 \vec{i}) + (\frac{5}{2} \vec{j} - 5 \vec{j}) \\ \Leftrightarrow \vec{M N} = - 5 \vec{i} - \frac{5}{2} \vec{j} \end{array}$

Vậy $\vec{M N} = - 5 \vec{i} - \frac{5}{2} \vec{j}$ .

Luyện tập 1 trang 61 Toán 10: Tìm tọa độ của $\vec{0}$

Lời giải:

Vì: $\vec{0} = 0. \vec{i} + 0. \vec{j}$ nên $\vec{0}$ có tọa độ là (0;0).

2. BIỂU THỨC TOẠ ĐỘ CỦA CÁC PHÉP TOÁN VECTO

Hoạt động 3 trang 61 Toán 10: Trong mặt phẳng tọa độ Oxy, cho $\vec{u} = (2; - 3), \vec{v} = (4; 1), \vec{a} = (8; - 12)$

a) Hãy biểu thị mỗi vectơ $\vec{u}, \vec{v}, \vec{a}$ theo các vectơ $\vec{i}, \vec{j}$

b) Tìm tọa độ của các vectơ $\vec{u} + \vec{v}, 4. \vec{u}$

c) Tìm mối liên hệ giữa hai vectơ $\vec{u}, \vec{a}$

Phương pháp giải:

a) Vectơ $\vec{a}$ có tọa độ (x;y) thì $\vec{a} = x . \vec{i} + y . \vec{j}$

b) Bước 1: Tính $\vec{u} + \vec{v}, 4. \vec{u}$ theo các vectơ $\vec{i}, \vec{j}$

Bước 2: Suy ra tọa độ của các vectơ $\vec{u} + \vec{v}, 4. \vec{u}$

c) Quan sát biểu thị theo các vectơ $\vec{i}, \vec{j}$ của các vectơ $\vec{u}, \vec{a}$ để suy ra mối liên hệ.

Lời giải:

a) Ta có: $\vec{u} = (2; - 3)$

$\Rightarrow \vec{u} = 2. \vec{i} + (- 3) . \vec{j}$

Tương tự ta có: $\vec{v} = (4; 1), \vec{a} = (8; - 12)$

$\Rightarrow \vec{v} = 4. \vec{i} + 1. \vec{j}; \vec{a} = 8. \vec{i} + (- 12) . \vec{j}$

b) Ta có: ${\begin{cases} \vec{u} = 2. \vec{i} + (- 3) . \vec{j} \\ \vec{v} = 4. \vec{i} + 1. \vec{j} \end{cases}$ (theo câu a)

$\begin{array}{l} \Rightarrow {\begin{cases} \vec{u} + \vec{v} = (2. \vec{i} + (- 3) . \vec{j}) + (4. \vec{i} + 1. \vec{j}) \\ 4. \vec{u} = 4 (2. \vec{i} + (- 3) . \vec{j}) \end{cases} \\ \Leftrightarrow {\begin{cases} \vec{u} + \vec{v} = (2. \vec{i} + 4. \vec{i}) + ((- 3) . \vec{j} + 1. \vec{j}) \\ 4. \vec{u} = 4.2. \vec{i} + 4. (- 3) . \vec{j} \end{cases} \\ \Leftrightarrow {\begin{cases} \vec{u} + \vec{v} = 6. \vec{i} + (- 2) . \vec{j} \\ 4. \vec{u} = 8. \vec{i} + (- 12) . \vec{j} \end{cases} \end{array}$

c) Vì ${\begin{cases} 4. \vec{u} = 8. \vec{i} + (- 12) . \vec{j} \\ \vec{a} = 8. \vec{i} + (- 12) . \vec{j} \end{cases}$ nên ta suy ra $4. \vec{u} = \vec{a}$