Với giải Câu hỏi trang 65 Toán 10 Tập 1 Kết nối tri thức trong Bài 10: Vecto trong mặt phẳng toạ độ học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Toán 10 Kết nối tri thức trang 65 Bài 10: Vecto trong mặt phẳng toạ độ
Bài 4.16 trang 65 Toán 10: Trong mặt phẳng tọa độ Oxy, cho các điểm M(1; 3), N(4; 2)
a) Tính độ dài các đoạn thẳng OM, ON, MN.
b) Chứng minh rằng tam giác OMN vuông cân.
Phương pháp giải:
Độ dài vectơlà
Lời giải:
a) Ta có: M(1; 3) và N (4; 2)
b) Dễ thấy: cân tại M.
Lại có:
Theo định lí Pythagore đảo, ta có vuông tại M.
Vậy vuông cân tại M.
a) Tìm mối liên hệ giữa các vectơ và .
b) Các điểm O, M, N có thẳng hàng hay không?
c) Tìm điểm P(x; y) để OMNP là một hình bình hành.
Phương pháp giải:
b) Các điểm O, M, N thẳng hàng khi và chỉ khi hai vectơ cùng phương
c) OMNP là một hình hành khi và chỉ khi
Lời giải:
a) Ta có: và
Lại có: M (-3; 6), N(3; -3)
Dễ thấy:
b) Ta có: ( do M(-3; 6)) và (do N (3; -3)).
Hai vectơ này không cùng phương (vì ).
Do đó các điểm O, M, N không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
c) Các điểm O, M, N không thẳng hàng nên OMNP là một hình hành khi và chỉ khi .
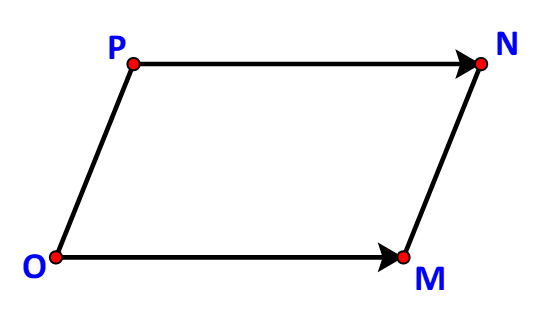
Do nên
Vậy điểm cần tìm là P (6; -9).
Bài 4.18 trang 65 Toán 10: Trong mặt phẳng tọa độ Oxy, cho các điểm A(1; 3), B(2; 4), C(-3; 2).
a) Hãy giải thích vì sao các điểm A, B, C không thẳng hàng.
b) Tìm tọa độ trung điểm M của đoạn thẳng AB.
c) Tìm tọa độ trọng tâm G của tam giác ABC.
d) Tìm điểm D(x; y) để O(0; 0) là trọng tâm của tam giác ABD.
Phương pháp giải:
a) Các điểm A, B, C thẳng hàng khi và chỉ khi hai vectơ cùng phương
b) Trung điểm M của đoạn thẳng AB có tọa độ là
c) Trọng tâm G của tam giác ABC có tọa độ là
d) Để O(0; 0) là trọng tâm của tam giác ABD thì
Lời giải:
a) Ta có:
Hai vectơ này không cùng phương (vì ).
Do đó các điểm A, B, C không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
b) Trung điểm M của đoạn thẳng AB có tọa độ là
c) Trọng tâm G của tam giác ABC có tọa độ là
d) Để O(0; 0) là trọng tâm của tam giác ABD thì
Vậy tọa độ điểm D là (-3; -7).
Tàu khởi hành từ vị trí A(1; 2) chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu thị bởi vectơ . Xác định vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.
Phương pháp giải:
Lập luận chỉ ra
Lời giải:
Gọi B(x; y) là vị trí của tàu (trên mặt phẳng tọa độ) tại thời điểm sau khi khởi hành 1,5 giờ.
Do tàu khởi hành từ A đi chuyển với vận tốc được biểu thị bởi vectơ nên cứ sau mỗi giờ, tàu đi chuyển được một quãng bằng .
Vậy sau 1,5 giờ tàu di chuyển tới B, ta được:
Vậy sau 1,5 tàu ở vị trí (trên mặt phẳng tọa độ) là B(5,5; 8).

Phương pháp giải:
+) Quân mã đi theo đường chéo hình chữ nhật dài 3 ô, rộng 2 ô.
Bước 1: Đánh dấu các vị trí trên bàn cờ mà quân mã có thể đi ở nước cờ tiếp theo.
Bước 2: Chiếu vuông góc xuống các trục Ox, Oy để xác định tọa độ.
Lời giải:
a) Quân mã đi theo đường chéo hình chữ nhật có chiều dài 3 ô, chiều rộng 2 ô.
Do đó, từ vị trí hiện tại, quân mã có thể đi đến các vị trí A, B, C, D, E, F như dưới đây:

A có tọa độ (3; 3)
B có tọa độ (3; 1)
C có tọa độ (2; 0)
D có tọa độ (0; 0)
E có tọa độ (0; 4)
F có tọa độ (2; 4)
Vậy quân mã có thể đi đến các vị trí A(3;3), B(3;1), C(2;0), D(0;0), E(0;4), F(2;4).
Xem thêm các bài giải Toán 10 Kết nối tri thức hay, chi tiết khác:
Câu hỏi mở đầu trang 60 Toán 10:Một bản tin dự báo thời tiết thể hiện đường đi trong 12 giờ của một cơn bão trên một mặt phẳng tọa độ...
Hoạt động 1 trang 60 Toán 10: Trên trục số Ox, gọi A là điểm biểu diễn số 1 và đặt...
Hoạt động 2 trang 61 Toán 10: Trong Hình 4.33:....
Luyện tập 1 trang 61 Toán 10: Tìm tọa độ của...
Hoạt động 3 trang 61 Toán 10: Trong mặt phẳng tọa độ Oxy, cho...
Hoạt động 4 trang 62 Toán 10: Trong mặt phẳng tọa độ Oxy, cho điểm...
Hoạt động 5 trang 62 Toán 10: Trong mặt phẳng tọa độ Oxy, cho các điểm...
Luyện tập 2 trang 63 Toán 10: Trong mặt phẳng tọa độ Oxy, cho hai điểm A(2; 1), B(3; 3)....
Bài 4.16 trang 65 Toán 10: Trong mặt phẳng tọa độ Oxy, cho các điểm M(1; 3), N(4; 2)...
Bài 4.18 trang 65 Toán 10: Trong mặt phẳng tọa độ Oxy, cho các điểm A(1; 3), B(2; 4), C(-3; 2)....
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.