Với giải Câu hỏi trang 96 Toán 10 Tập 2 Kết nối tri thức trong Bài tập cuối năm học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem: 

Toán 10 Kết nối tri thức trang 96: Bài tập cuối năm

Bài 8 trang 96 SGK Toán 10 Tập 2: a) Biểu diễn miền nghiệm D của hệ bất phương trình bậc nhất hai ẩn sau:  

$\left\{\begin{array}{l}x+y\le 6\\ 2x-y\le 2\\ x\ge 0\\ y\ge 0\end{array}\right.$.

b) Từ kết quả câu a, tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y trên miền D.

Lời giải:

a) Biểu diễn miền nghiệm D của hệ bất phương trình bậc nhất hai ẩn sau: $\left\{\begin{array}{l}x+y\le 6\\ 2x-y\le 2\\ x\ge 0\\ y\ge 0\end{array}\right.$  

+) Vẽ đường thẳng x + y = 6 trên mặt phẳng Oxy, lấy điểm O(0; 0), ta thấy 0 + 0 < 6 nên miền nghiệm của bất phương trình x + y ≤ 6 là nửa mặt phẳng có bờ là đường thẳng x + y = 6 chứa điểm O(0; 0) kể cả biên. 

+) Vẽ đường thẳng 2x – y = 2 trên mặt phẳng Oxy, lấy điểm O(0; 0), ta thấy 2 . 0 – 0 ≤ 2 nên miền nghiệm của bất phương trình 2x – 2 ≤ 2 là nửa mặt phẳng có bờ là đường thẳng 2x – y = 2 chứa điểm O(0; 0) kể cả biên. 

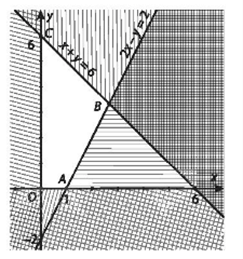
Miền nghiệm của hệ $\left\{\begin{array}{l}x+y\le 6\\ 2x-y\le 2\\ x\ge 0\\ y\ge 0\end{array}\right.$như hình trên. 

b) Từ kết quả câu a, ta thấy miền nghiệm của hệ bất phương trình là miền tứ giác OABC kể cả các cạnh của tứ giác. Tọa độ của các đỉnh của tứ giác OABC là: O(0; 0), A(1; 0),$B\left(\frac{8}{3};\frac{10}{3}\right)$ , C(0; 6). 

Ta có: F(x; y) = 2x + 3y. 

F(0; 0) = 0; F(1; 0) = 2; ; F(0; 6) = 18. 

Vậy giá trị lớn nhất của F(x; y) = 2x + 3y trên miền D là 18. Giá trị nhỏ nhất của F(x; y) = 2x + 3y trên miền D là 0. 

Bài 9 trang 96 SGK Toán 10 Tập 2: Cho hàm số y = f(x) = ax2 + bx + c với đồ thị là parabol (P) có đỉnh$I\left(\frac{5}{2};-\frac{1}{4}\right)$ và đi qua điểm A(1; 2).

a) Biết rằng phương trình của parabol có thể viết dưới dạng y = a(x – h)2 + k, trong đó I(h, k) là tọa độ đỉnh của parabol. Hãy xác định phương trình của parabol (P) đã cho và vẽ parabol này.

b) Từ parabol (P) đã vẽ ở câu a, hãy cho biết khoảng đồng biến và khoảng nghịch biến của hàm số y = f(x).

c) Giải bất phương trình f(x) ≥ 0.

Lời giải:

a) Vì parabol có đỉnh $I\left(\frac{5}{2};-\frac{1}{4}\right)$ nên ta có h =$\frac{5}{2}$ và k =$-\frac{1}{4}$ . Suy ra phương trình của parabol (P) có dạng: $y=a{\left(x-\frac{5}{2}\right)}^2-\frac{1}{4}$. 

Vì parabol (P) đi qua điểm A(1; 2) nên ta có $2=a{\left(1-\frac{5}{2}\right)}^2-\frac{1}{4}$. Suy ra a = 1. 

Vậy parabol (P) có phương trình là $y=1.{\left(x-\frac{5}{2}\right)}^2-\frac{1}{4}$ hay y = x2 – 5x + 6. 

* Vẽ parabol (P): 

Parabol có đỉnh $I\left(\frac{5}{2};-\frac{1}{4}\right)$, hệ số a = 1> 0 nên parabol có bề lõm hướng lên trên.

Phương trình trục đối xứng: $x=\frac{5}{2}$. 

Giao điểm của (P) với trục tung có tọa độ là B(0; 6). 

Phương trình x2 – 5x + 6 = 0 có hai nghiệm x = 2 và x = 3. Vậy giao điểm của (P) với trục hoành là C(2; 0) và D(3; 0). 

Vẽ đường cong đi qua các điểm trên ta được parabol (P).

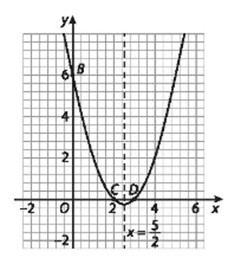
b) Từ parabol (P) đã vẽ ở câu a, ta có hàm số y = x2 – 5x + 6 đồng biến trên khoảng $\left(\frac{5}{2};+\infty \right)$ và nghịch biến trên khoảng $\left(-\infty ;\frac{5}{2}\right)$. 

c) Ta có: f(x) ≥ 0 

⇔ x2 – 5x + 6 ≥ 0

⇔ x ≤ 2 hoặc x ≥ 3 (từ đồ thị suy ra)

Vậy tập nghiệm của bất phương trình là S = (– ∞; 2] ∪ [3; + ∞). 

Bài 10 trang 96 SGK Toán 10 Tập 2: Giải các phương trình chứa căn thức sau:

a) $\sqrt{2x^2-6x+3}=\sqrt{x^2-3x+1}$; 

b) $\sqrt{x^2+18x-9}=2x-3$. 

Lời giải:

a) Bình phương hai vế của phương trình $\sqrt{2x^2-6x+3}=\sqrt{x^2-3x+1}$ ta được: 

2x2 – 6x + 3 = x2 – 3x + 1 

⇔ x2 – 3x + 2 = 0 

⇔ x2 – x – 2x + 2 = 0 

⇔ x(x – 1) – 2(x – 1) = 0 

⇔ (x – 2)(x – 1) = 0 

⇔ x = 2 hoặc x = 1

Thử lại vào phương trình đã cho ta thấy không có giá trị nào thỏa mãn. 

Vậy phương trình vô nghiệm. 

b) Bình phương hai vế của phương trình $\sqrt{x^2+18x-9}=2x-3$, ta được: 

x2 + 18x – 9 = (2x – 3)2 

⇔ x2 + 18x – 9 = 4x2 – 12x + 9

⇔ 3x2 – 30x + 18 = 0 

⇔ x2 – 10x + 6 = 0 

⇔ x = 5 + $\sqrt{19}$ hoặc x = $5-\sqrt{19}$. 

Thử lại vào phương trình đã cho ta thấy chỉ có giá trị x = 5 +$\sqrt{19}$ thỏa mãn. 

Vậy nghiệm của phương trình là x = 5 +$\sqrt{19}$ . 

Bài 11 trang 96 SGK Toán 10 Tập 2: Từ các chữ số 0; 1; 2;.....; 9 có thể lập được tất cả bao nhiêu số tự nhiên nhỏ hơn 1 000, chia hết cho 5 và gồm các chữ số khác nhau?

Lời giải:

Các số tự nhiên nhỏ hơn 1 000, chia hết cho 5 là các số tự nhiên nhỏ hơn 1 000 có chữ số tận cùng là 0 hoặc 5. Ta có các trường hợp sau:

• Trường hợp 1. Số có một chữ số: Chỉ có 0 và 5 thỏa mãn. Do đó có 2 số có một chữ số thỏa mãn đề bài. 

• Trường hợp 2. Số có hai chữ số khác nhau dạng: $\overline{ab}$, $a\ne b$. 

Khi b = 5 ta có a ≠ 0 và a ≠ 5. Do đó có 8 cách chọn a, tương ứng có 8 số lập được. 

Khi b = 0 ta có a ∈ {1; 2; 3; …; 9}. Do đó có 9 cách chọn a, tương ứng có 9 số lập được. 

Vậy có 8 + 9 = 17 số có hai chữ số khác nhau thỏa mãn đề bài. 

• Trường hợp 3. Số có ba chữ số khác nhau dạng: $\overline{abc},a\ne b\ne c$. 

Khi c = 5 ta có a ≠ 0 và a ≠ 5, a có 8 cách chọn; b ∈ {0; 1; 2; 3; …; 9}\{a; b}, b có 8 cách chọn. Do đó có 1 . 8 . 8 = 64 số. 

Khi c = 0 ta có a, b ∈ {1; 2; 3; …; 9}, a ≠ b. Do đó có $1.A_9^2=72$ số. 

Vậy có 64 + 72 = 136 số có ba chữ số khác nhau thỏa mãn đề bài. 

Từ ba trường hợp trên ta có các số tự nhiên nhỏ hơn 1 000 thỏa mãn yêu cầu của đề bài là 2 + 17 + 136 = 155 (số). 

Bài 12 trang 96 SGK Toán 10 Tập 2: Viết khai triển nhị thức Newton của (2x – 1)n, biết n là số tự nhiên thỏa mãn $A_n^2+24C_n^1=140$.

Lời giải:

Ta có: $A_n^2+24C_n^1=140$(1)

Điều kiện: n ≥ 2. 

Khi đó (1) $\iff \frac{n!}{\left(n-2\right)!}+24.\frac{n!}{1!\left(n-1\right)!}=140$

$\iff n\left(n-1\right)+24.n=140$

⇔ n2 – n + 24n = 140 

⇔ n2 + 23n – 140 = 0 

⇔ n = 5 hoặc n = – 28.

Do đó ta có n = 5 thỏa mãn điều kiện. 

Khi đó ta có khai triển nhị thức Newton:

(2x – 1)5 = [2x + (– 1)]5

$=C_5^0.{\left(2x\right)}^5+C_5^1.{\left(2x\right)}^4.\left(-1\right)+C_5^2.{\left(2x\right)}^3.{\left(-1\right)}^2+C_5^3.{\left(2x\right)}^2.{\left(-1\right)}^3$

$+C_5^4.\left(2x\right).{\left(-1\right)}^4+C_5^5.{\left(-1\right)}^5$

= 32x5 – 80x4 + 80x3 – 40x2 + 10x – 1.

Bài 13 trang 96 SGK Toán 10 Tập 2: Từ các công thức tính diện tích tam giác đã được học, hãy chứng minh rằng, trong tam giác ABC, ta có

$r=\frac{\sqrt{\left(b+c-a\right)\left(c+a-b\right)\left(a+b-c\right)}}{2\sqrt{a+b+c}}$.

Lời giải:

Gọi S, p lần lượt là diện tích, nửa chu vi của tam giác ABC. 

Ta có: $p=\frac{a+b+c}{2}$. 

Theo các công thức về diện tích tam giác, ta có: 

$S=p.r=\sqrt{p.\left(p-a\right).\left(p-b\right).\left(p-c\right)}$. 

Từ đó suy ra:$r=\frac{S}{p}=\frac{\sqrt{p.\left(p-a\right).\left(p-b\right).\left(p-c\right)}}{p}$

$$\begin{gathered} =\sqrt{\frac{p.\left(p-a\right).\left(p-b\right).\left(p-c\right)}{p^2}}=\sqrt{\frac{\left(p-a\right).\left(p-b\right).\left(p-c\right)}{p}} \\ =\sqrt{\frac{\left(\frac{a+b+c}{2}-a\right).\left(\frac{a+b+c}{2}-b\right).\left(\frac{a+b+c}{2}-c\right)}{\frac{a+b+c}{2}}} \\ =\sqrt{\frac{\frac{b+c-a}{2}.\frac{a+c-b}{2}.\frac{a+b-c}{2}}{\frac{a+b+c}{2}}}=\sqrt{\frac{1}{8}\mathrm{.2.}\frac{\left(b+c-a\right).\left(a+c-b\right).\left(a+b-c\right)}{a+b+c}} \\ =\sqrt{\frac{\left(b+c-a\right).\left(a+c-b\right).\left(a+b-c\right)}{4\left(a+b+c\right)}}=\frac{{\displaystyle \sqrt{\left(b+c-a\right).\left(c+a-b\right).\left(a+b-c\right)}}}{{\displaystyle 2\sqrt{a+b+c}}} \end{gathered}$$. 

Vậy r $=\frac{\sqrt{\left(b+c-a\right).\left(c+a-b\right).\left(a+b-c\right)}}{2\sqrt{a+b+c}}$(điều phải chứng minh). 

Bài 14 trang 96 SGK Toán 10 Tập 2: Cho hình vuông ABCD có cạnh bằng a. Gọi M, N tương ứng là trung điểm của các cạnh AB, BC.

a) Biểu thị các vectơ $\overrightarrow{DM},\overrightarrow{AN}$ theo các vectơ $\overrightarrow{AB},\overrightarrow{AD}$. 

b) Tính $\overrightarrow{DM}\cdot \overrightarrow{AN}$ và tìm góc giữa hai đường thẳng DM và AN.

Lời giải:

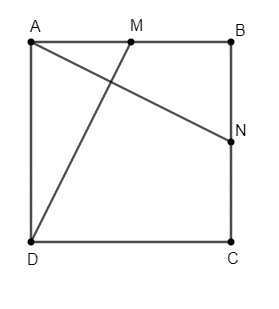
a) Vì M là trung điểm của AB nên $\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}$. 

Do đó, ta có: $\overrightarrow{DM}=\overrightarrow{AM}-\overrightarrow{AD}=\frac{1}{2}\overrightarrow{AB}-\overrightarrow{AD}$. 

Vì N là trung điểm của BC nên $\overrightarrow{BN}=\frac{1}{2}\overrightarrow{BC}$. 

Do ABCD là hình vuông nên $\overrightarrow{BC}=\overrightarrow{AD}$. Khi đó, $\overrightarrow{BN}=\frac{1}{2}\overrightarrow{AD}$. 

Theo quy tắc ba điểm ta có: $\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}=\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$. 

b) Do ABCD là hình vuông nên ta có: AB = AD = a,$\overrightarrow{AB}\cdot \overrightarrow{AD}=0$ (AB ⊥ AD). 

Từ đó suy ra $\overrightarrow{DM}\cdot \overrightarrow{AN}=\left(\frac{1}{2}\overrightarrow{AB}-\overrightarrow{AD}\right)\cdot \left(\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}\right)$

$=\frac{1}{2}{\left(\overrightarrow{AB}\right)}^2+\frac{1}{4}\overrightarrow{AB}\cdot \overrightarrow{AD}-\overrightarrow{AD}\cdot \overrightarrow{AB}-\frac{1}{2}{\left(\overrightarrow{AD}\right)}^2$. 

$=\frac{1}{2}A{B}^2+\frac{1}{4}\cdot 0-0-\frac{1}{2}A{D}^2$

$=\frac{1}{2}\left(A{B}^2-A{D}^2\right)=0$

Do đó: $\overrightarrow{DM}\cdot \overrightarrow{AN}=0\iff \overrightarrow{DM}\perp \overrightarrow{AN}\iff DM\perp AN$.

Vậy góc giữa hai đường thẳng  DM và AN bằng 90°. 

Bài 15 trang 96 SGK Toán 10 Tập 2: Trong mặt phẳng tọa độ, cho tam giác ABC có ba đỉnh A(– 1; 3), B(1; 2), C(4; – 2).

a) Viết phương trình đường thẳng BC.

b) Tính diện tích tam giác ABC.

c) Viết phương trình đường tròn có tâm A và tiếp xúc với đường thẳng BC.

Lời giải:

a) Ta có: $\overrightarrow{BC}=\left(4-1;\left(-2\right)-2\right)=\left(3;-4\right)$. 

Do đó đường thẳng BC có 1 vectơ chỉ phương là $\overrightarrow{u_{BC}}=\left(3;-4\right)$. 

Suy ra đường thẳng BC có 1 vectơ pháp tuyến là $\overrightarrow{n_{BC}}=\left(4;3\right)$. 

Phương trình đường thẳng BC là 4.(x – 1) + 3(y – 2) = 0 hay 4x + 3y – 10 = 0. 

b) Ta có: $BC=\sqrt{3^2+{\left(-4\right)}^2}=5$. 

Khoảng cách từ A đến đường thẳng BC là 

d(A, BC) = $\frac{\left|4\cdot \left(-1\right)+3\cdot 3-10\right|}{\sqrt{4^2+3^2}}=\frac{5}{5}=1$. 

Độ dài đường cao kẻ từ A của tam giác ABC chính bằng khoảng cách từ A đến đường thẳng BC. Do đó, diện tích tam giác ABC là

SABC = $\frac{1}{2}d\left(A,BC\right)\cdot BC=\frac{1}{2}\mathrm{.1.5}=\frac{5}{2}$. 

c) Đường tròn có tâm A và tiếp xúc với đường thẳng BC có bán kính bằng khoảng cách từ A đến đường thẳng BC, do đó R = d(A, BC) = 1. 

Vậy phương trình đường tròn là (x + 1)2 + (y – 3)2 = 1. 

Bài 16 trang 96 SGK Toán 10 Tập 2: Trên mặt phẳng tọa độ, hai vật thể khởi hành cùng lúc tại hai điểm A(1; 1) và B(– 1; 21) với các vectơ vận tốc tương ứng là $\overrightarrow{v_A}=\left(1;2\right),\overrightarrow{v_B}=\left(1;-4\right)$. Hỏi hai vật thể đó có gặp nhau hay không?

Lời giải:

Vật A khởi hành từ điểm A(1; 1) với vectơ vận tốc là $\overrightarrow{v_A}=\left(1;2\right)$, do đó phương trình chuyển động của vật A là $\left\{\begin{array}{l}x=1+t\\ y=1+2t\end{array}\right.$. 

Vật B khởi hành từ điểm B(– 1; 21) với vectơ vận tốc là $\overrightarrow{v_B}=\left(1;-4\right)$, do đó phương trình chuyển động của vật B là $\left\{\begin{array}{l}x=-1+t^{\text{'}}\\ y=21-4t^{\text{'}}\end{array}\right.$. 

Giả sử 2 vật có thể gặp nhau, nghĩa là tồn tại thời điểm m (m > 0) để hai vật ở cùng một vị trí. 

Vị trí của vật khởi hành từ điểm A tại thời điểm m là $\left\{\begin{array}{l}x=1+m\\ y=1+2m\end{array}\right.$. 

Vị trí của vật khởi hành từ điểm B tại thời điểm m là $\left\{\begin{array}{l}x=-1+m\\ y=21-4m\end{array}\right.$. 

Vì hai vật có cùng vị trí tại thời điểm m nên ta có hệ phương trình $\left\{\begin{array}{l}1+m=-1+m\\ 1+2m=21-4m\end{array}\right.$. 

Giải hệ phương trình trên, ta thấy, phương trình đầu 1 + m = – 1 + m  ⇔ 1 = – 1 (vô lí), vậy phương trình này vô nghiệm, do đó hệ vô nghiệm.  

Vậy hai vật không thể gặp nhau.