Với giải Câu hỏi trang 103 Toán 10 Tập 2 Cánh Diều trong Bài tập cuối chương 7 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem:
Nội dung bài viết
Toán 10 Cánh Diều trang 103: Bài tập cuối chương 7
A. (1; –1).
B. (1; 1).
C. (– 1; 1).
D. (– 1; – 1).
Lời giải:
Đáp án đúng là: C.
Ta có: →AB=(2−3;5−4). Vậy →AB=(−1;1).
Bài 2 trang 103 Toán lớp 10 Tập 2: Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng Δ: 2x – 3y + 4 = 0?
A. →n1=(3;2).
B. →n2=(2;3).
C. →n3=(3;−2).
D. →n4=(2;−3).
Lời giải:
Đáp án đúng là: D.
Đường thẳng ∆: 2x – 3y + 4 = 0 có một vectơ pháp tuyến là →n=(2;−3)
Bài 3 trang 103 Toán lớp 10 Tập 2: Tọa độ tâm I của đường tròn (C): (x + 6)2 + (y – 12)2 = 81 là:
A. (6; – 12).
B. (– 6; 12).
C. (– 12; 6).
D.(12; – 6).
Lời giải:
Đáp án đúng là: B.
Ta có: (x + 6)2 + (y – 12)2 = 81 ⇔ (x – (– 6))2 + (y – 12)2 = 92.
Do đó đường tròn (C) có tâm I(– 6; 12).
A. 1.
B. 2.
C. 3.
D. 4.
Lời giải:
Đáp án đúng là: D.
Khoảng cách từ điểm A(1; 1) đến đường thẳng Δ: 3x + 4y + 13 = 0 là
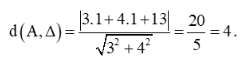
a) Tìm tọa độ của các vectơ →OM,→MN,→MP ;
b) Tính tích vô hướng →MN.→MP ;
c) Tính độ dài các đoạn thẳng MN, MP;
d) Tính cos^NMP ;
e) Tìm tọa độ trung điểm I của NP và trọng tâm G của tam giác MNP.
Lời giải:
a) Tọa độ của vectơ →OM chính là tọa độ của điểm M(2; 1), do đó →OM=(2;1).
Ta có: →MN=(−1−2;3−1), do đó →MN=(−3;2).
→MP=(4−2;2−1), do đó →MP=(2;1).
b) Ta có: →MN.→MP=(−3).2+2.1=−6+2=−4.
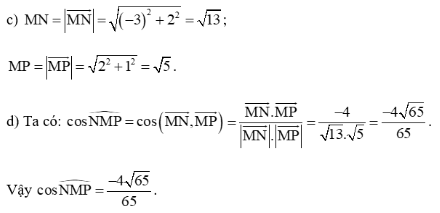
e) Tọa độ trung điểm I của NP là xI=(−1)+42=32;yI=3+22=52 hay I(32;52).
Tọa độ trọng tâm G của tam giác MNP là xG=2+(−1)+43=53;yG=1+3+23=63=2 hay G(53;2).
Bài 6 trang 103 Toán lớp 10 Tập 2: Lập phương trình tổng quát và phương trình tham số của đường thẳng d trong mỗi trường hợp sau:
a) d đi qua điểm A(– 3; 2) và có một vectơ pháp tuyến là →n=(2;−3);
b) d đi qua điểm B(– 2; – 5) và có một vectơ chỉ phương là →u=(−7;6);
c) d đi qua hai điểm C(4; 3) và D(5; 2).
Lời giải:
a) Đường thẳng d đi qua điểm A(– 3; 2) và có một vectơ pháp tuyến là →n=(2;−3), do đó phương trình tổng quát của đường thẳng d là: 2(x – (– 3)) – 3(y – 2) = 0 hay 2x – 3y + 12 = 0.
Đường thẳng d có một vectơ pháp tuyến là →n=(2;−3), do đó nó có một vectơ chỉ phương là →u=(3;2).

Đường thẳng d có một vectơ chỉ phương là , suy ra nó có một vectơ pháp tuyến là →n=(6;7).
Vậy phương trình tổng quát của đường thẳng d là 6(x + 2) + 7(y + 5) = 0 hay 6x + 7y + 47 = 0.
c) Ta có: →CD=(5−4;2−3)=(1;−1).
Đường thẳng d đi qua 2 điểm C, D nên có một vectơ chỉ phương là →u=→CD=(1;−1).

Đường thẳng d có một vectơ pháp tuyến là →n=(1;1).
Vậy phương trình tổng quát của đường thẳng d là 1(x – 4) + 1(y – 3) = 0 hay x + y – 7 = 0.
Bài 7 trang 103 Toán lớp 10 Tập 2: Lập phương trình đường tròn (C) trong mỗi trường hợp sau:
a) (C) có tâm I(– 4; 2) và bán kính R = 3;
b) (C) có tâm P(3; – 2) và đi qua điểm E(1; 4);
c) (C) có tâm Q(5; – 1) và tiếp xúc với đường thẳng Δ: 3x + 4y – 1 = 0;
d) (C) đi qua ba điểm A(– 3; 2), B(– 2; – 5) và D(5; 2).
Lời giải:
a) Đường tròn (C) có tâm I(– 4; 2) và bán kính R = 3.
Vậy phương trình đường tròn (C) là (x – (– 4))2 + (y – 2)2 = 32 hay (x + 4)2 + (y – 2)2 = 9.
b) Đường tròn (C) có tâm P(3; – 2) và đi qua điểm E(1; 4) nên bán kính của đường tròn chính bằng khoảng cách từ P đến E.
Do đó, R = PE = √(1−3)2+(4−(−2))2=√4+36=√40.
Vậy phương trình đường tròn (C) là (x−3)2+(y−(−2))2=(√40)2 hay (x – 3)2 + (y + 2)2 = 40.
c) Đường tròn (C) có tâm Q(5; – 1) và tiếp xúc với đường thẳng Δ: 3x + 4y – 1 = 0, do đó bán kính của đường tròn chính bằng khoảng cách từ tâm Q đến đường thẳng ∆.
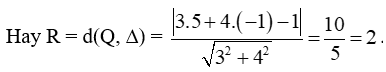
Vậy phương trình đường tròn (C) là (x – 5)2 + (y – (– 1))2 = 22 hay (x – 5)2 + (y + 1)2 = 4.
d) Đường tròn (C) đi qua ba điểm A(– 3; 2), B(– 2; – 5) và D(5; 2).
Giả sử tâm của đường tròn là điểm I(a; b).
Ta có IA = IB = ID ⇔ IA2 = IB2 = ID2.
Vì IA2 = IB2, IB2 = ID2 nên
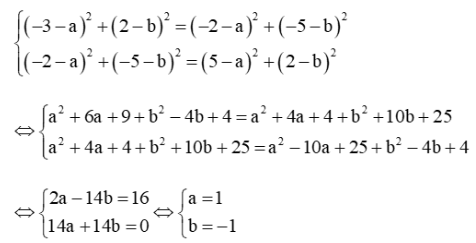
Đường tròn tâm I(1; – 1) bán kính R = ID = √(5−a)2+(2−b)2 =√(5−1)2+(2+1)2=5
Phương trình đường tròn (C) là (x−1)2+(y−(−1))2=52.
Vậy phương trình đường tròn (C) là (x−1)2+(y+1)2=25.
Xem thêm các bài giải sách bài tập Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 2 trang 103 Toán lớp 10 Tập 2: Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng Δ: 2x – 3y + 4 =0...
Bài 3 trang 103 Toán lớp 10 Tập 2: Tọa độ tâm I của đường tròn (C): (x + 6)2 + (y – 12)2 = 81 là...
Bài 7 trang 103 Toán lớp 10 Tập 2: Lập phương trình đường tròn (C) trong mỗi trường hợp sau...
Bài 8 trang 104 Toán lớp 10 Tập 2: Quan sát Hình 64 và thực hiện các hoạt động sau...
Bài 9 trang 104 Toán lớp 10 Tập 2: Cho hai đường thẳng: Δ1:√3x+y−4=0,Δ2:x+√3y−2√3=0...
Bài 11 trang 104 Toán lớp 10 Tập 2: Cho tam giác AF1F2, trong đó A(0; 4), F1(– 3; 0), F2(3; 0)...
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.