Với giải Câu hỏi trang 104 Toán 10 Tập 2 Cánh Diều trong Bài tập cuối chương 7 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 10. Mời các bạn đón xem: 

Toán 10 Cánh Diều trang 104: Bài tập cuối chương 7

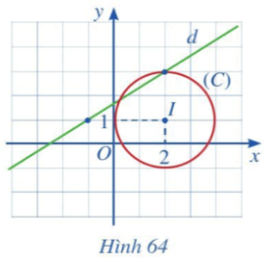
Bài 8 trang 104 Toán lớp 10 Tập 2: Quan sát Hình 64 và thực hiện các hoạt động sau:

a) Lập phương trình đường thẳng d;

b) Lập phương trình đường tròn (C);

c) Lập phương trình tiếp tuyến của đường tròn (C) tại điểm $M\left(2+\sqrt{2};1+\sqrt{2}\right)$.

Lời giải:

a) Quan sát Hình 64 ta thấy đường thẳng d đi qua hai điểm A(– 1; 1) và B(2; 3).

Ta có: $\overrightarrow{AB}=\left(3;2\right)$.

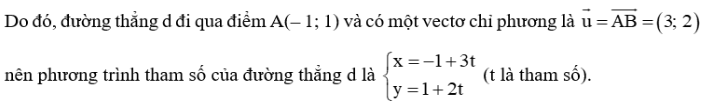
b) Quan sát Hình 64 ta thấy đường tròn (C) có tâm I(2; 1) và bán kính R = 2, do đó phương trình đường tròn (C) là (x – 2)² + (y – 1)² = 2² hay (x – 2)² + (y – 1)² = 4.

c) Phương trình tiếp tuyến của đường tròn (C) tại điểm $M\left(2+\sqrt{2};1+\sqrt{2}\right)$ là

$\left(2+\sqrt{2}-2\right)\left(x-\left(2+\sqrt{2}\right)\right)+\left(1+\sqrt{2}-1\right)\left(y-\left(1+\sqrt{2}\right)\right)=0$

$\iff \sqrt{2}x-2\sqrt{2}-2+\sqrt{2}y-\sqrt{2}-2=0$

$\iff \sqrt{2}x+\sqrt{2}y-3\sqrt{2}-4=0$

$\iff x+y-3-2\sqrt{2}=0$

Vậy phương trình tiếp tuyến cần lập là $x+y-3-2\sqrt{2}=0$.

Bài 9 trang 104 Toán lớp 10 Tập 2: Cho hai đường thẳng: ${\Delta }_1:\sqrt{3}x+y-4=0,{\Delta }_2:x+\sqrt{3}y-2\sqrt{3}=0.$

a) Tìm tọa độ giao điểm của hai đường thẳng Δ₁ và Δ₂.

b) Tính số đo góc giữa hai đường thẳng Δ₁ và Δ₂.

Lời giải:

a) Tọa độ giao điểm của hai đường thẳng Δ₁ và Δ₂ là nghiệm của hệ phương trình

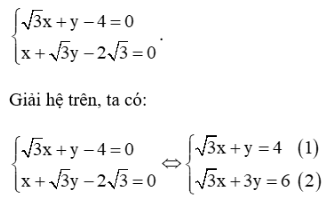
Lấy (2) trừ vế theo vế cho (1) ta được: 3y – y = 6 – 4 ⇔ 2y = 2 ⇔ y = 1.

Thay y = 1 vào (1) ta được: $\sqrt{3}x+1=4\iff \sqrt{3}x=3\iff x=\sqrt{3}$.

Do đó, hệ trên có nghiệm duy nhất $\left(\sqrt{3};1\right)$.

Vậy tọa độ giao điểm của hai đường thẳng Δ₁ và Δ₂ là $\left(\sqrt{3};1\right)$.

b) Đường thẳng ∆₁ có vectơ pháp tuyến là $\overrightarrow{n_1}=\left(\sqrt{3};1\right)$.

Đường thẳng ∆₂ có vectơ pháp tuyến là $\overrightarrow{n_2}=\left(1;\sqrt{3}\right)$.

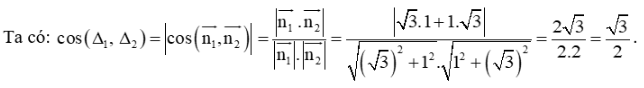
Do đó, (∆₁, ∆₂) = 30°.

Bài 10 trang 104 Toán lớp 10 Tập 2: Cho biết mỗi đường conic có phương trình dưới đây là đường conic dạng nào (elip, hypebol, parabol) và tìm tọa độ tiêu điểm của đường conic đó.

a) y2 = 18x;

b) $\frac{x^2}{64}+\frac{y^2}{25}=1$;

c) $\frac{x^2}{9}-\frac{y^2}{16}=1$.

Lời giải:

a) Ta có: y² = 18x ⇔ y² = 2 . 9 . x

Do đó, phương trình trên là phương trình của parabol với p = 9.

Ta có $\frac{p}{2}=\frac{9}{2}$ nên tọa độ tiêu điểm của parabol là $F\left(\frac{9}{2};0\right)$.

b) $\frac{x^2}{64}+\frac{y^2}{25}=1$$\iff \frac{x^2}{8^2}+\frac{y^2}{5^2}=1$.

Do đó, phương trình trên là phương trình của elip với a = 8, b = 5 thỏa mãn a > b > 0.

Ta có: c² = a² – b² = 64 – 25 = 39, suy ra c = $\sqrt{39}$.

Vậy tọa độ các tiêu điểm của elip là $F_1\left(-\sqrt{39};0\right),\overrightarrow{F_2}\left(\sqrt{39};0\right)$.

c) $\frac{x^2}{9}-\frac{y^2}{16}=1\iff \frac{x^2}{3^2}-\frac{y^2}{4^2}=1$.

Do đó, phương trình trên là phương trình của hypebol với a = 3, b = 4 thỏa mãn a > 0, b > 0.

Ta có: c² = a² + b² = 9 + 16 = 25, suy ra c = 5.

Vậy tọa độ các tiêu điểm của hypebol là F₁(– 5; 0) và F₂(5; 0).

Bài 11 trang 104 Toán lớp 10 Tập 2: Cho tam giác AF₁F₂, trong đó A(0; 4), F₁(– 3; 0), F₂(3; 0).

a) Lập phương trình tổng quát của các đường thẳng AF₁ và AF₂.

b) Lập phương trình đường tròn ngoại tiếp của tam giác AF₁F₂.

c) Lập phương trình chính tắc của elip (E) có hai tiêu điểm là F₁, F₂ sao cho (E) đi qua A.

Lời giải:

a) Ta có: $\overrightarrow{A{F}_1}=\left(-3;-4\right)$ là một vectơ chỉ phương của đường thẳng AF1, do đó đường thẳng này có một vectơ pháp tuyến là $\overrightarrow{n_1}=\left(4;-3\right)$.

Vậy phương trình tổng quát đường thẳng AF₁ là 4(x – 0) – 3(y – 4) = 0 hay 4x – 3y + 12 = 0.

Lại có: $\overrightarrow{A{F}_2}=\left(3;-4\right)$ là một vectơ chỉ phương của đường thẳng AF₂, do đó đường thẳng này có một vectơ pháp tuyến là $\overrightarrow{n_2}=\left(4;3\right)$.

Vậy phương trình tổng quát đường thẳng AF₂ là 4(x – 0) + 3(y – 4) = 0 hay 4x + 3y – 12 = 0.

b) Đường tròn ngoại tiếp tam giác AF₁F₂ là đường tròn đi qua 3 điểm A, F₁, F₂.

Giả sử tâm của đường tròn là điểm I(a; b).

Ta có IA = IF1 = IF2 ⇔ IA2 =$I{F}_1^2$ = $I{F}_2^2$ .

Vì IA₂ = $I{F}_1^2$, $I{F}_1^2$ = $I{F}_2^2$ nên

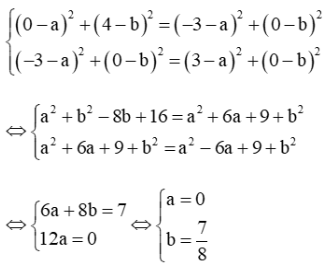
Đường tròn tâm $I\left(0;\frac{7}{8}\right)$ bán kính R = IA = $\sqrt{{\left(0-a\right)}^2+{\left(4-b\right)}^2}$$=\sqrt{{\left(4-\frac{7}{8}\right)}^2}=\frac{25}{8}$.

Phương trình đường tròn (C) là ${\left(x-0\right)}^2+{\left(y-\frac{7}{8}\right)}^2={\left(\frac{25}{8}\right)}^2$.

Vậy phương trình đường tròn (C) là $x^2+{\left(y-\frac{7}{8}\right)}^2=\frac{625}{64}$.

c) Phương trình chính tắc của elip (E) có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\left(a>b>0\right)$.

Elip (E) đi qua điểm A(0; 4), thay tọa độ điểm A vào phương trình elip ta được $\frac{0^2}{a^2}+\frac{4^2}{b^2}=1\iff b^2=4^2\Rightarrow b=4\left(dob>0\right)$.

Elip (E) có hai tiêu điểm là F₁(– 3; 0), F₂(3; 0), do đó c = 3.

Suy ra a² – b² = c² hay a² – 4² = 3² ⇔ a² = 9 + 16 = 25 = 5², suy ra a = 5 (do a > 0).

Khi đó a > b > 0 (do 5 > 4 > 0), vậy a = 5, b = 4 là thỏa mãn.

Vậy phương trình elip (E) cần lập là $\frac{x^2}{5^2}+\frac{y^2}{4^2}=1hay\frac{x^2}{25}+\frac{y^2}{16}=1$.

Bài 12 trang 104 Toán lớp 10 Tập 2: Trên màn hình ra đa của đài kiểm soát không lưu sân bay A có hệ trục toạ độ Oxy (Hình 65), trong đó đơn vị trên mỗi trục tính theo ki-lô-mét và đài kiểm soát được coi là gốc toạ độ 0(0 ; 0). Nếu máy bay bay trong phạm vi cách đài kiểm soát 500 km thì sẽ hiển thị trên màn hình ra đa như một điểm chuyển động trong mặt phẳng với hệ trục toạ độ Oxy.

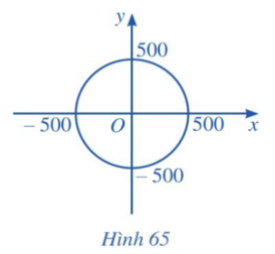
Một máy bay khởi hành từ sân bay B lúc 14 giờ. Sau thời gian t (giờ), vị trí của máy bay được xác định bởi điểm M có toạ độ như sau:

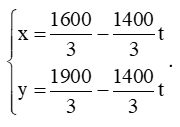
a) Tìm vị trí của máy bay lúc 14 giờ 30 phút. Thời điểm này máy bay đã xuất hiện trên màn hình ra đa chưa?

b) Lúc mấy giờ máy bay bay gần đài kiểm soát không lưu nhất? Tính khoảng cách giữa máy bay và đài kiểm soát không lưu lúc đó.

c) Máy bay ra khỏi màn hình ra đa vào thời gian nào?.

Lời giải:

a) Lúc 14 giờ 30 phút máy bay đã bay được: 14 giờ 30 phút – 14 giờ = 30 phút = 0,5 giờ.

Vậy vị trí của máy bay lúc 14 giờ 30 phút ở tại điểm có tọa độ E(300; 400).

Ta có: $\overrightarrow{OE}=\left(300;400\right)$ nên $OE=\sqrt{{300}^2+{400}^2}=500$, hay khoảng cách từ đài kiểm soát không lưu O đến vị trí E của máy bay lúc 14 giờ 30 phút là 500 km.

Vậy thời điểm này máy bay đã xuất hiện trên màn hình ra đa.

Gọi H là hình chiếu của O đến đường thẳng d. Khi đó OH là khoảng cách ngắn nhất từ O đến H hay chính là tại vị trí H máy bay bay gần đài kiểm soát không lưu nhất.

Ta có H thuộc d nên tọa độ $H\left(\frac{1600}{3}-\frac{1400}{3}t;\frac{1900}{3}-\frac{1400}{3}t\right)$.

Khi đó, $\overrightarrow{OH}=\left(\frac{1600}{3}-\frac{1400}{3}t;\frac{1900}{3}-\frac{1400}{3}t\right)$.

Lại có đường thẳng d có vectơ chỉ phương là $\overrightarrow{u_d}=-\frac{3}{1400}\left(-\frac{1400}{3};-\frac{1400}{3}\right)=\left(1;1\right)$.

Vì OH ⊥ d nên $\overrightarrow{OH}.\overrightarrow{u_d}=0\iff \left(\frac{1600}{3}-\frac{1400}{3}t\right).1+\left(\frac{1900}{3}-\frac{1400}{3}t\right).1=0$.

Khi đó H(– 50; 50).

Do đó, OH = $50\sqrt{2}$.

Ta có: t = $\frac{5}{4}$ giờ = 1 giờ 15 phút.

Vậy máy bay bay gần đài kiểm soát không lưu nhất lúc: 14 giờ + 1 giờ 15 phút = 15 giờ 15 phút và khoảng cách giữa máy bay và đài kiểm soát không lưu lúc này là $50\sqrt{2}$ km.

c) Gọi $K\left(\frac{1600}{3}-\frac{1400}{3}t;\frac{1900}{3}-\frac{1400}{3}t\right)$ là vị trí máy bay ra khỏi màn hình ra đa.

Khi đó OK > 500 km.

Ta có: $\overrightarrow{OK}=\left(\frac{1600}{3}-\frac{1400}{3}t;\frac{1900}{3}-\frac{1400}{3}t\right)$

Do đó, $OK=\sqrt{{\left(\frac{1600}{3}-\frac{1400}{3}t\right)}^2+{\left(\frac{1900}{3}-\frac{1400}{3}t\right)}^2}$.

Hay $\sqrt{{\left(\frac{1600}{3}-\frac{1400}{3}t\right)}^2+{\left(\frac{1900}{3}-\frac{1400}{3}t\right)}^2}>500$

Suy ra ${\left(\frac{1600}{3}-\frac{1400}{3}t\right)}^2+{\left(\frac{1900}{3}-\frac{1400}{3}t\right)}^2>250000$

$\iff \frac{3920000}{9}{t}^2-\frac{9800000}{9}t+\frac{3920000}{9}>0$

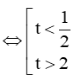
Ta có t = $\frac{1}{2}$ giờ = 30 phút.

Vậy máy bay bay ra khỏi màn hình ra đa vào khoảng thời gian từ 14 giờ đến trước 14 giờ 30 phút và sau 16 giờ.