SBT Toán 10 Kết nối tri thức trang 27: Bài tập cuối chương 6

Với giải Câu hỏi trang 27 SBT Toán 10 Tập 2 Kết nối tri thức trong Bài tập cuối chương 6 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập SBT Toán 10. Mời các bạn đón xem:

SBT Toán 10 Kết nối tri thức trang 27: Bài tập cuối chương 6

Bài 6.61 trang 27 sách bài tập Toán 10: Cho hình chữ nhật ABCD có AB = 6 cm, AD = 13 cm. Tìm vị trí điểm M trên cạnh AD sao cho BM = 2MD

Lời giải:

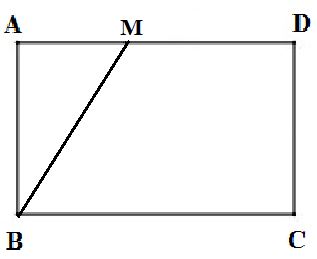
Gọi x (cm) (0 < x < 13) là độ dài AM.

Khi đó MD = 13 – x (cm) và BM = (cm)

Theo giả thiết, BM = 2MD (*)

Bình phương 2 vế PT (*) ta có:

hoặc x = 8

Kết hợp với điều kiện, PT (*) có nghiệm duy nhất x = 8

Vậy với AM = 8 cm thì BM = 2MD.

Bài 6.62 trang 27 sách bài tập Toán 10: Trong Vật lí ta biết rằng, khi một vật được ném xiên với vận tốc ban đầu v₀, góc ném hợp với phương ngang Ox một góc $α$ , nếu ta bỏ qua sức cản của không khí và gió, vật chỉ chịu tác dụng của trọng lực với gia tốc trọng trường $g \approx 9, 8$ m/s², thì độ cao y (so với mặt đất) của vật phụ thuộc vào khoảng cách theo phương ngang x (tính đến mặt đất tại điểm ném) theo một hàm số bậc hai cho bởi công thức

$y = \frac{- g}{2 v_{0}^{2} \cos^{2} α} x^{2} + x \tan α$

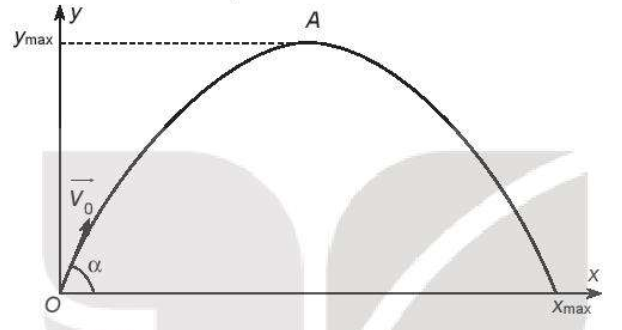
Như vậy quỹ đạo chuyển động của vật là một phần của đường parabol. Hãy xác định

a) Các hệ số a, b và c của hàm số bậc hai này

b) Độ cao lớn nhất mà vật có thể đạt được

c) Giả sử vận tốc ban đầu v0 không đổi. Từ kết quả câu b) hãy xác định góc ném α để độ cao của vật đạt giá trị lớn nhất

d) Một quả bóng được đá từ mặt đất lên cao với vận tốc ban đầu v0 = 20 m/s và góc đá so với phương ngang là 450. Khi quả bóng ở độ cao trên 5 m thì khoảng cách theo phương ngang từ vị trí của quả bóng đến vị trí đá bóng nằm trong khoảng nào (làm tròn kết quả đến hàng phần trăm)?

Lời giải:

a) Hàm số bậc hai $y = \frac{- g}{2 v_{0}^{2} \cos^{2} α} x^{2} + x \tan α$ có các hệ số:

$a = \frac{- g}{2 v_{0}^{2} \cos^{2} α} < 0$ ; $b = \tan α$ ; c = 0

b) Tam thức bậc hai $\frac{- g}{2 v_{0}^{2} \cos^{2} α} x^{2} + x \tan α$ có $Δ = \tan^{2} α$

$\Rightarrow$ Tung độ đỉnh của parabol là $- \frac{Δ}{4 a} = \frac{\tan^{2} α}{\frac{4 g}{2 v_{0}^{2} \cos^{2} α}} = \frac{v_{0}^{2} \tan^{2} α . \cos^{2} α}{2 g} = \frac{v_{0}^{2} \sin^{2} α}{2 g}$

Vậy độ cao lớn nhất mà vật có thể đạt được là $\frac{v_{0}^{2} \sin^{2} α}{2 g}$ m

c) $\frac{v_{0}^{2} \sin^{2} α}{2 g} \leq \frac{v_{0}^{2}}{2 g}$ $\Rightarrow y_{max} = \frac{v_{0}^{2}}{2 g}$ khi $\sin α = 1 \Leftrightarrow α = 90^{0}$

Vậy với góc ném $α = 90^{0}$ thì độ cao của vật đạt GTLN

d) Với v₀ = 20 m/s, $α = 45^{0}$ , $g = 9, 8$ m/s² ta có:

$y = \frac{- 9, 8}{{2.20}^{2} . \cos^{2} 45^{0}} x^{2} + x . \tan 45^{0} \Leftrightarrow y = - \frac{49}{2000} x^{2} + x$

Theo giả thiết, $y > 5 \Leftrightarrow - \frac{49}{2000} x^{2} + x - 5 > 0 \Leftrightarrow 5, 83 < x < 34, 98$

Vậy khi quả bóng ở độ cao trên 5 m thì khoảng cách theo phương ngang từ vị trí của quả bóng đến vị trí đá bóng nằm trong khoảng $x \in (5, 83; 34, 98)$ mét.

Bài 6.63 trang 27 sách bài tập Toán 10: Một công ti kinh doanh máy tính cầm tay thấy rằng khi bán máy ở mức giá x (nghìn đồng) một chiếc thì số lượng máy bán được n cho bởi phương trình n = 1 200 000 – 1 200x.

a) Tìm công thức biểu diễn doanh thu R như là hàm số của đơn giá x. Tìm miền xác định của hàm số R = R(x)

b) Máy tính được bán ở đơn giá nào sẽ cho doanh thu lớn nhất? Tính doanh thu lớn nhất và số máy tính bán được trong trường hợp đó

c) Với đơn giá nào thì công ti sẽ đạt được doanh thu trên 200 tỉ đồng (làm tròn đến nghìn đồng)?

Lời giải:

a) Ta có: $R (x) = x . n \Leftrightarrow R (x) = x (1200000 - 1200 x) \Leftrightarrow R (x) = - 1200 x^{2} + 1200000 x$