Toptailieu.vn xin giới thiệu 05 câu trắc nghiệm Bài tập cuối chương 6 Kết nối tri thức (có đáp án 2023) CHỌN LỌC, hay nhất giúp học sinh lớp 10 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

05 câu trắc nghiệm Bài tập cuối chương 6 Kết nối tri thức (có đáp án 2023) CHỌN LỌC

Lý thuyết

I. Hàm số

1. Định nghĩa

Cho D ⊂ R, D ≠ Ø. Một hàm số xác định trên D là một quy tắc f cho tương ứng mỗi số x ∈ D với một và duy nhất chỉ một số y ∈ R. Ta kí hiệu:

f: D → R

x → y = f(x)

Tập hợp D được gọi là tập xác định (hay miền xác định), x được gọi là biến số, y_o = f(x_o) tại x = x_o.

Một hàm số có thể được cho bằng một công thức hay bằng biểu đồ hay bằng bảng.

Lưu ý rằng, khi cho nột hàm số bằng công thức mà không nói rõ tập xác định thì ta ngầm hiểu tập xác định D là tập hợp các số x ∈ R mà các phép toán trong công thức có nghĩa.

2. Đồ thị

Đồ thị của hàm số:

f: D → R

x → y = f(x)

là tập hợp các điểm (x;f(x)), x ∈ D trên mặt phẳng tọa độ.

3. Sự biến thiên

Hàm số y = f(x) là đồng biến trên khoảng (a;b) nếu với mọi x₁, x₂ ∈ (a;b) mà x₁ < x₂ ⇔ f(x₁) < f(x₂) hay x₁ ≠ x₂ ta có .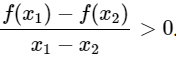

Hàm số y = f(x) là nghịch biến trên khoảng (a;b) nếu với mọi x₁, x₂ ∈ (a;b) mà x₁ < x₂ ⇒ f(x₁) > f(x₂) hay x₁ ≠ x₂ ta có .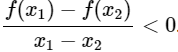

4. Tính chẵn lẻ của hàm số

Hàm số

f: D → R

x → y = f(x)

được gọi là hàm số chẵn nếu: x ∈ D ⇒ -x ∈ D và f(-x) = f(x), là hàm số lẻ nếu x ∈ D ⇒ -x ∈ D và f(-x) = -f(x).

II. Hàm số bậc hai

1. Hàm số bậc hai

Định nghĩa

Hàm số bậc hai được cho bởi công thức:

y = ax² + bx + c (a ≠ 0)

có tập xác định D = R và biệt thức Δ = b² - 4ac

Chiều biến thiên:

Nếu a > 0 thì hàm số y = ax² + bx + c:

Bảng biến thiên:

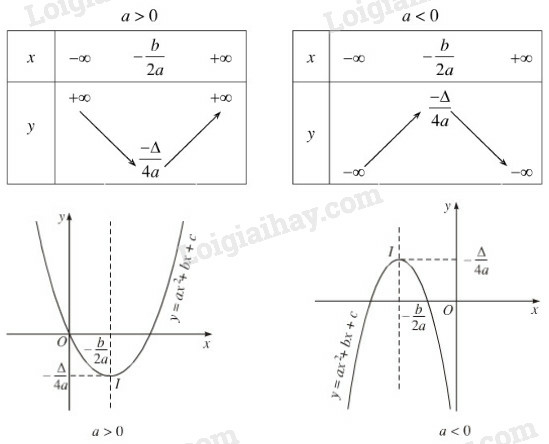
2. Đồ thị hàm số bậc hai

Đồ thị hàm số y = ax² + bx + c (a ≠ 0) là đường parabol có:

+) đỉnh là điểm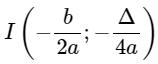 

+) trục đối xứng là đường thẳng .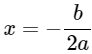

+) Bề lõm của Parabol quay lên trên nếu a > 0 và xuống dưới nếu a < 0.

+) Giao điểm với trục tung: A(0;c).

+) Hoành độ giao điểm với trục hoành (nếu có) là nghiệm của phương trình ax² + bx + c = 0.

* Cách vẽ

Cách 1: (Dùng cho mọi trường hợp)

Bước 1: Xác định tọa độ đỉnh I

Bước 2: Vẽ trục đối xứng

Bước 3: Xác định tọa độ các giao điểm của Parabol cới trục tung và trục hoành (nếu có)

Bước 4: Vẽ parabol (lưu ý dấu của hệ số a - liên quan đến bề lõm của Parabol)

Cách 2: (sử dụng khi đã có đồ thị hàm số y = ax²)

Đồ thị hàm số y = ax² + bx + c (a ≠ 0) suy ra từ đồ thị hàm số y = ax² bằng cách:

+ Tịnh tiến song song với trục hoành |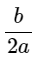| đơn vị về bên trái nếu  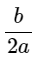 > 0, về bên phải nếu  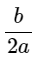< 0.

+ Tịnh tiến song song với trục tung |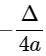| đơn vị lên trên nếu 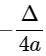> 0, và xuống dưới nếu  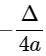< 0.

III. Dấu của tam thức bậc hai

1. Tam thức bậc hai (một ẩn)

Tam thức bậc hai (đối với x) là biểu thức dạng ax² + bx + c. Trong đó a, b, c là nhũng số cho trước với a ≠ 0.

Nghiệm của phương trình ax² + bx + c = 0 được gọi là nghiệm của tam thức bậc hai f(x) = ax² + bx + c; Δ = b² - 4ac và Δ' = b'² - ac theo thứ tự được gọi là biệt thức và biệt thức thu gọn của tam thức bậc hai f(x) = ax² + bx + c.

2. Dấu của tam thức bậc hai

Định lí.

Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0) có biệt thức Δ = b² - 4ac.

- Nếu Δ < 0 thì f(x) luôn cùng dấu với hệ số a với mọi x ∈ R.

- Nếu Δ = 0 thì f(x) có nghiệm kép x = -.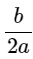

Khi đó f(x) có cùng dấu với hệ số a với mọi x ≠ -.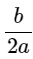

- Nếu Δ > 0, f(x) có 2 nghiệm x₁, x₂ (x₁ < x₂) và luôn cùng dấu với hệ số a với mọi x ∈ (-∞;x₁) ∪ (x₂;+∞) và luôn trái dấu với hệ số a với mọi x ∈ (x₁;x₂)

Chú ý:

Dấu của tam thức bậc hai được thể hiện trong bảng sau

Nhận xét: Cho tam thức bậc hai ax² + bx + c

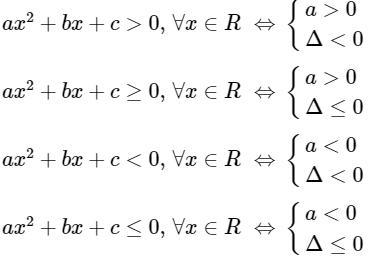
IV. Phương trình quy về phương trình bậc hai

1. Các kiến thức cần nhớ

a. Phương trình trùng phương

+)  Phương trình trùng phương là phương trình có dạng ax⁴ + bx² + c = 0 (a ≠ 0)   

+) Cách giải: Đặt ẩn phụ t = x² (t ≥ 0) để đưa phương trình về phương trình bậc hai:  at² + bt + c = 0 (a ≠ 0)

b. Phương trình chứa ẩn ở mẫu thức

Để giải phương trình chứa ẩn ở mẫu thức, ta có các bước giải như sau:

Bước 1. Tìm điều kiện xác định của ẩn của phương trình.

Bước 2. Quy đồng mẫu thức hai vế rồi khử mẫu.

Bước 3. Giải phương trình vừa nhận được ở bước 2.

Bước 4. So sánh các nghiệm tìm được ở bước 3 với điều kiện xác định và kết luận.

c. Phương trình đưa về dạng phương trình tích

Để giải phương trình đưa về dạng tích, ta có các bước giải như sau:

Bước 1. Phân tích vế trái thành nhân tử, vế phải bằng 0.

Bước 2. Xét từng nhân tử bằng 0 để tìm nghiệm.

d) Sự tương giao giữa đường thẳng và parabol

Sự tương giao giữa đường thẳng d:y = mx + n và parabol (P): y = ax² (a ≠ 0) 

Hình minh họa

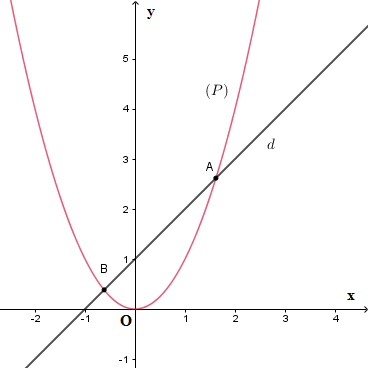
Số giao điểm của đường thẳng d và parabol (P) là số nghiệm của phương trình hoành độ giao điểm

ax² = mx + n ⇔ ax² - mx - n = 0 (*)

+) Phương trình (*) có hai nghiệm phân biệt (Δ > 0) thì d cắt (P) tại hai điểm phân biệt

+) Phương trình (*) có nghiệm kép (Δ = 0) thì d tiếp xúc với (P).

+) Phương trình (*) vô nghiệm (Δ < 0) thì d không cắt (P)

2. Các dạng toán thường gặp

Dạng 7: Xác định số giao điểm của đường thẳng d:y = mx + n và parabol (P):y = ax² (a ≠ 0)

Phương pháp:

Số giao điểm của đường thẳng d và parabol (P) là số nghiệm của phương trình hoành độ giao điểm

ax² = mx + n ⇔ ax² - mx - n = 0 (*)

+) Phương trình (*) có hai nghiệm phân biệt (Δ > 0) thì d cắt (P) tại hai điểm phân biệt

+) Phương trình (*) có nghiệm kép (Δ = 0)thì d tiếp xúc với (P).

+) Phương trình (*) vô nghiệm (Δ < 0)thì d không cắt (P)

Dạng 8: Tìm tọa độ giao điểm của đường thẳng d:y = mx + n và parabol (P):y = ax² (a ≠ 0)

Phương pháp:

Xét phương trình hoành độ giao điểm ax² = mx + n ⇔ ax² - mx - n = 0 (*)

Giải phương trình (*) tìm được x suy ra y. Tọa độ giao điểm là (x;y).

Dạng 9: Xác định tham số m để đường thẳng d:y = mx + n và parabol (P):y = ax² (a ≠ 0) cắt nhau tại điểm thỏa mãn điều kiện cho trước .

Phương pháp:

+) Đường thẳng d cắt (P) tại hai điểm phân biệt nằm bên trái trục tung ⇔ phương trình (*) có hai nghiệm âm phân biệt ⇔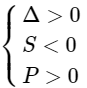 

+) Đường thẳng d cắt (P) tại hai điểm phân biệt cùng nằm bên phải trục tung ⇔ phương trình (*) có hai nghiệm dương phân biệt ⇔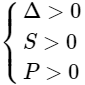 

+) Đường thẳng d cắt (P) tại hai điểm phân biệt nằm khác phía trục tung ⇔ phương trình (*) có hai nghiệm trái dấu ⇔ ac < 0

+) Đường thẳng d cắt (P) tại hai điểm có tọa độ thỏa mãn biểu thức cho trước (thường biến đổi biểu thức để sử dụng hệ thức Vi-et)

Dạng 10: Bài toán liên quan đến diện tích tam giác, diện tích hình thang và chiều cao.

Phương pháp:

Ta vận dụng linh hoạt các cách phân chia diện tích và công thức tính diện tích tam giác, hình thang để làm bài.

Bài tập

Câu 1: Tập xác định của hàm số 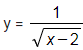 là:

A. D = [2; + ∞).

B. D = (2; + ∞).

C. D = ℝ \{2}.

D. D = ℝ.

Lời giải: 

Đáp án đúng là: B.

Biểu thức  có nghĩa khi x – 2 > 0 ⇔ x > 2.

Vậy tập xác định của hàm số đã cho là D = (2; + ∞).

Câu 2: Parabol y = – x2 + 2x + 3 có đỉnh là

A. I(– 1; 0).

B. I(3; 0).

C. I(0; 3).

D. I(1; 4).

Lời giải: 

Đáp án đúng là: D.

Parabol y = – x2 + 2x + 3 có các hệ số: a = – 1; b = 2, c = 3.

Ta có:   và y(1) = – 12 + 2 . 1 + 3 = 4.

Vậy tọa độ đỉnh của parabol là I(1; 4).

Câu 3: Hàm số y = x2 – 5x + 4

A. Đồng biến trên khoảng (1; + ∞).

B. Đồng biến trên khoảng (– ∞; 4).

C. Nghịch biến trên khoảng (– ∞; 1).

D. Nghịch biến trên khoảng (1; 4).

Lời giải: 

Đáp án đúng là: C.

Hàm số y = x2 – 5x + 4 có các hệ số a = 1 > 0, b = – 5, c = 4.

Ta có:  .

Do đó hàm số đã cho nghịch biến trên khoảng   và đồng biến trên khoảng  .

Mà (– ∞; 1)   nên hàm số đã cho nghịch biến trên khoảng (– ∞; 1).

Câu 4: Bất phương trình x2 – 2mx + 4 > 0 nghiệm đúng với mọi x ∈ ℝ khi

A. m = – 1.

B. m = – 2.

C. m = 2.

D. m > 2.

Lời giải: 

Đáp án đúng là: A.

Xét tam thức bậc hai f(x) = x2 – 2mx + 4 có hệ số a = 1 > 0, ∆' = (– m)2 – 1 . 4 = m2 – 4.

Để f(x) > 0 (cùng dấu với hệ số a) với mọi x ∈ ℝ thì ∆' < 0 hay m2 – 4 < 0.

⇔ m2 < 4 ⇔ – 2 < m < 2.

Trong các đáp án đã cho, ta thấy đáp án m = – 1 là thỏa mãn – 2 < m < 2.  

Câu 5: Tập nghiệm của phương trình   là

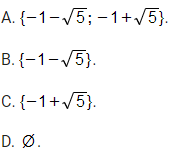
Lời giải: 

Đáp án đúng là: C.

Bình phương hai vế của phương trình  ta được:

2x2 – 3 = x2 – 2x + 1

⇔ x2 + 2x – 4 = 0

⇔  .

Lần lượt thay các giá trị trên vào phương trình đã cho, ta thấy x =   thỏa mãn.

Vậy tập nghiệm của phương trình đã cho là S = {}.

Xem thêm các bài giải Trắc nghiệm Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 18: Phương trình quy về phương trình bậc hai

Bài 19: Phương trình đường thẳng

Bài 20: Vị trí tương đối giữa hai đường thẳng. Góc và khoảng cách

Bài 21: Đường tròn trong mặt phẳng tọa độ

Bài 22: Ba đường conic