SBT Toán 10 Kết nối tri thức Bài 18: Phương trình quy về phương trình bậc hai

Nguyễn Thanh Huyền Ngày: 13-01-2023 Lớp 10

602

Toptailieu biên soạn và giới thiệu giải sách bài tập Toán 10 Bài 18 (Kết nối tri thức): Phương trình quy về phương trình bậc hai hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm các bài tập từ đó nâng cao kiến thức và biết cách vận dụng phương pháp giải vào các bài tập trong SBT Toán 10 Bài 18.

SBT Toán 10 Kết nối tri thức Bài 18: Phương trình quy về phương trình bậc hai

Bài 6.28 trang 21 sách bài tập Toán 10: Giải các phương trình sau:

a) $\sqrt{- x^{2} + 77 x - 212} = \sqrt{x^{2} + x - 2}$

b) $\sqrt{x^{2} + 25 x - 26} = \sqrt{x - x^{2}}$

c) $\sqrt{4 x^{2} + 8 x - 37} = \sqrt{- x^{2} - 2 x + 3}$

Lời giải:

a) $\sqrt{- x^{2} + 77 x - 212} = \sqrt{x^{2} + x - 2}$ (1)

Bình phương 2 vế của (1) ta được:

$- x^{2} + 77 x - 212 = x^{2} + x - 2$ $\Leftrightarrow 2 x^{2} - 76 x + 210 = 0$ $\Leftrightarrow x = 3$ hoặc x = 35

+) Thay x = 3 vào PT (1): $\sqrt{- 3^{2} + 77.3 - 212} = \sqrt{3^{2} + 3 - 2} \Leftrightarrow \sqrt{10} = \sqrt{10}$ , thỏa mãn

+) Thay x = 35 vào PT (1): $\sqrt{- 35^{2} + 77.35 - 212} = \sqrt{35^{2} + 35 - 2} \Leftrightarrow \sqrt{1258} = \sqrt{1258}$ , thỏa mãn

Vậy PT (1) có 2 nghiệm là x = 3; x = 35

b) $\sqrt{x^{2} + 25 x - 26} = \sqrt{x - x^{2}}$ (2)

Bình phương 2 vế của (2) ta được:

$x^{2} + 25 x - 26 = x - x^{2} \Leftrightarrow 2 x^{2} + 24 x - 26 = 0 \Leftrightarrow x = - 13$ hoặc x = 1

+) Thay x = -13 vào PT (2): $\sqrt{{(- 13)}^{2} + 25. (- 13) - 26} = \sqrt{(- 13) - {(- 13)}^{2}} \Leftrightarrow \sqrt{- 182} = \sqrt{- 182}$ , vô lí

+) Thay x = 1 vào PT (2): $\sqrt{1^{2} + 25.1 - 26} = \sqrt{1 - 1^{2}} \Leftrightarrow \sqrt{0} = \sqrt{0}$ , thỏa mãn

Vậy PT (2) có nghiệm duy nhất x = 1

c) $\sqrt{4 x^{2} + 8 x - 37} = \sqrt{- x^{2} - 2 x + 3}$ (3)

Bình phương 2 vế của (3) ta được:

$4 x^{2} + 8 x - 37 = - x^{2} - 2 x + 3 \Leftrightarrow 5 x^{2} + 10 x - 40 = 0 \Leftrightarrow x = - 4$ hoặc x = 2

+) Thay x = -4 vào PT (3): $\sqrt{4. {(- 4)}^{2} + 8. (- 4) - 37} = \sqrt{- {(- 4)}^{2} - 2. (- 4) + 3} \Leftrightarrow \sqrt{- 5} = \sqrt{- 5}$ , vô lí

+) Thay x = 2 vào PT (3): $\sqrt{{4.2}^{2} + 8.2 - 37} = \sqrt{- 2^{2} - 2.2 + 3} \Leftrightarrow \sqrt{- 5} = \sqrt{- 5}$ , vô lí

Vậy PT (3) vô nghiệm

Bài 6.29 trang 21 sách bài tập Toán 10: Giải các phương trình sau:

a) $\sqrt{2 x^{2} - 13 x + 16} = 6 - x$

b) $\sqrt{3 x^{2} - 33 x + 55} = x - 5$

c) $\sqrt{- x^{2} + 3 x + 1} = x - 4$

Lời giải:

a) $\sqrt{2 x^{2} - 13 x + 16} = 6 - x$ (1)

Bình phương 2 vế của (1) ta được:

$2 x^{2} - 13 x + 16 = x^{2} - 12 x + 36 \Leftrightarrow x^{2} - x - 20 = 0 \Leftrightarrow x = - 4$ hoặc x = 5

+) Thay x = -4 vào vế phải PT (1): 6- (-4) = 10 > 0

+) Thay x = 5 vào vế phải PT (1): 6 – 5 = 1 > 0

Vậy PT (1) có hai nghiệm phân biệt là x = -4; x = 5

b) $\sqrt{3 x^{2} - 33 x + 55} = x - 5$ (2)

Bình phương 2 vế của (2) ta được:

$3 x^{2} - 33 x + 55 = x^{2} - 10 x + 25 \Leftrightarrow 2 x^{2} - 23 x + 30 = 0 \Leftrightarrow x = \frac{3}{2}$ hoặc x = 10

+) Thay $x = \frac{3}{2}$ vào vế phải PT (2): $\frac{3}{2} - 5 = - \frac{7}{2} < 0$

+) Thay x = 10 vào vế phải PT (2): 10 – 5 = 5 > 0

Vậy PT (2) có nghiệm duy nhất x = 10

c) $\sqrt{- x^{2} + 3 x + 1} = x - 4$ (3)

Bình phương 2 vế PT (3) ta được:

$- x^{2} + 3 x + 1 = x^{2} - 8 x + 16 \Leftrightarrow 2 x^{2} - 11 x + 15 = 0$ $\Leftrightarrow x = \frac{5}{2}$ hoặc x = 3

+) Thay $x = \frac{5}{2}$ vào vế phải PT (3): $\frac{5}{2} - 4 = - \frac{3}{2} < 0$

+) Thay x = 3 vào vế phải PT (3): 3 – 4 = -1 < 0

Vậy PT (3) vô nghiệm

Bài 6.30 trang 21 sách bài tập Toán 10: Giải các phương trình sau:

a) $\sqrt{2 x - 3} = x - 3$

b) $(x - 3) \sqrt{x^{2} + 4} = x^{2} - 9$

Lời giải:

a) $\sqrt{2 x - 3} = x - 3$ (1)

Bình phương 2 vế của (1) ta được:

$2 x - 3 = x^{2} - 6 x + 9 \Leftrightarrow x^{2} - 8 x + 12 = 0 \Leftrightarrow x = 2$ hoặc x = 6

+) Thay x = 2 vào vế phải PT (1): 2 – 3 = -1 < 0

+) Thay x = 5 vào vế phải PT (1): 6 – 3 = 3 > 0

Vậy PT (1) nghiệm duy nhất là x = 6

b) $(x - 3) \sqrt{x^{2} + 4} = x^{2} - 9$ $\Leftrightarrow (x - 3) \sqrt{x^{2} + 4} - (x^{2} - 9) = 0 \Leftrightarrow (x - 3) \sqrt{x^{2} + 4} - (x - 3) (x + 3) = 0$

$\Leftrightarrow (x - 3) (\sqrt{x^{2} + 4} - x - 3) = 0$

TH1: $x - 3 = 0 \Leftrightarrow x = 3$

TH2: $\sqrt{x^{2} + 4} - x - 3 = 0$ $\sqrt{x^{2} + 4} = x + 3$ (2)

Bình phương 2 vế của (2) ta được:

$x^{2} + 4 = x^{2} + 6 x + 9 \Leftrightarrow 6 x = - 5 \Leftrightarrow x = - \frac{5}{6}$

+) Thay $x = - \frac{5}{6}$ vào vế phải PT (2): $- \frac{5}{6} + 3 = \frac{13}{6} > 0$

Vậy PT đã cho có hai nghiệm phân biệt là $x = 3; x = - \frac{5}{6}$

Bài 6.31 trang 21 sách bài tập Toán 10: Tìm điều kiện của tham số m để phương trình sau có nghiệm:

(ảnh 1)

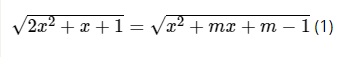
Lời giải:

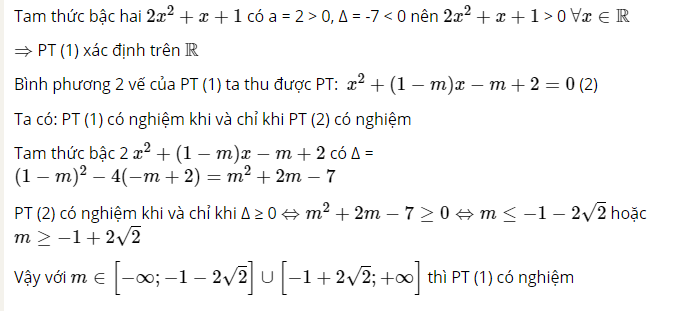
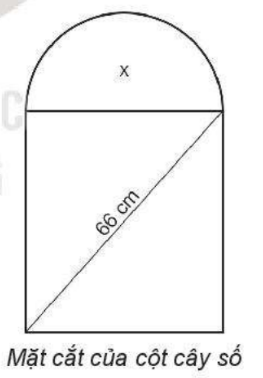
Bài 6.32 trang 21 sách bài tập Toán 10: Mặt cắt đứng của cột cây số trên quốc lộ có dạng nửa hình tròn ở phía trên và phía dưới có dạng hình chữ nhật (xem hình bên). Biết rằng đường kính của nửa hình tròn cũng là cạnh phía trên của hình chữ nhật và đường chéo của hình chữ nhật có độ dài 66 cm. Tìm kích thước của hình chữ nhật, biết rằng diện tích của phần nửa hình tròn bằng 0,3 lần diện tích của phần hình chữ nhật. Lấy $π = 3, 14$ và làm tròn kết quả đến chữ số thập phân thứ hai.

Lời giải:

Gọi x (cm) (0 < x < 66) là đường kính của nửa hình tròn

$\Rightarrow$ Kích thước còn lại của hình chữ nhật là y = $\sqrt{66^{2} - x^{2}} = \sqrt{4356 - x^{2}}$ (cm)

DIện tích của nửa hình tròn là: $S_{1} = \frac{1}{2} π . {(\frac{x}{2})}^{2} = \frac{3, 14}{8} x^{2}$ (cm²)

Diện tích hình chữ nhật là: $S_{2} = x \sqrt{4356 - x^{2}}$ (cm²)

Theo giả thiết, $S_{1} = 0, 3 S_{2} \Leftrightarrow \frac{3, 14}{8} x^{2} = 0, 3. x \sqrt{4356 - x^{2}}$

$\Leftrightarrow \frac{3, 14}{8} x^{2} - 0, 3. x \sqrt{4356 - x^{2}} = 0 \Leftrightarrow x (\frac{3, 14}{8} x - 0, 3 \sqrt{4356 - x^{2}})$ = 0

$\Leftrightarrow \frac{3, 14}{8} x - 0, 3 \sqrt{4356 - x^{2}} = 0$ (do x > 0) $\Leftrightarrow \sqrt{4356 - x^{2}} = \frac{157}{120} x$ (*)

Bình phương hai vế của (*) ta được: $4356 - x^{2} = \frac{24649}{14400} x^{2} \Leftrightarrow x^{2} \approx 1606, 35 \Leftrightarrow x \approx 40, 08$