Toptailieu.vn giới thiệu Giải bài tập Toán lớp 10 Bài 18: Phương trình quy về phương trình bậc hai sách Kết nối tri thức giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 10 Tập 2. Mời các bạn đón xem:

Toán 10 Kết nối tri thức Bài 18: Phương trình quy về phương trình bậc hai

1. Phương trình dạng

Câu hỏi trang 25 Toán 10

HĐ1 trang 25 SGK Toán 10 Tập 2: Cho phương trình $\sqrt{x^2-3x+2}=\sqrt{-x^2-2x+2}$

a) Bình phương hai vế của phương trình để khử căn và giải phương trình bậc hai nhận được

b) Thử lại các giá trị x tìm được ở câu a có thỏa mãn phương trình đã cho hay không

Lời giải:

a) Bình phương hai vế của phương trình$\sqrt{x^2-3x+2}=\sqrt{-x^2-2x+2}$ta được:

$x^2-3x+2=-x^2-2x+2$(1)

Giải phương trình trên ta có:

$(1)\iff 2x^2-x=0$

$\iff x(2x-1)=0$

$\iff x=0$ hoặc $x=\frac{1}{2}$

b) Thử lại ta có:

Với x=0, thay vào phương trình đã cho ta được: $\sqrt{0^2-3.0+2}=\sqrt{-0^2-2.0+2}\iff \sqrt{2}=\sqrt{2}$ (luôn đúng)

Với $x=\frac{1}{2}$, thay vào phương trình đã cho ta được:

$\sqrt{{\left(\frac{1}{2}\right)}^2-3.\frac{1}{2}+2}=\sqrt{-{\left(\frac{1}{2}\right)}^2-2.\frac{1}{2}+2}\iff \sqrt{\frac{3}{4}}=\sqrt{\frac{3}{4}}$ (luôn đúng)

Vậy các giá trị x tìm được ở câu a thỏa mãn phương trình đã cho

a) Bình phương hai vế và giải phương trình nhận được

b) Thử lại các giá trị x tìm được ở câu a có thỏa mãn phương trình đã cho hay không

Lời giải:

a) Bình phương hai vế của phương trình $\sqrt{26x^2-63x+38}=5x-6$ ta được:

$26x^2-63x+38=(5x-6{)}^2$

$\iff 26x^2-63x+38=25x^2-60x+36$

$\iff x^2-3x+2=0$

$\iff x=1$ hoặc $x=2$

b) Thử lại:

Với x = 1 thay vào phương trình đã cho ta được: 

$\sqrt{{26.1}^2-63.1+38}=5.1-6$

$\iff 1=-1$(vô lý)

Với x=2 thay vào phương trình đã cho ta được:

$\sqrt{{26.2}^2-63.2+38}=5.2-6$

$\iff \sqrt{16}=4\iff 4=4$ (luôn đúng)

Vậy giá trị x=2 thỏa mãn phương trình đã cho

Luyện tập 2 trang 26 SGK Toán 10 Tập 2: Giải các phương trình sau:

a) $\sqrt{2x^2+x+3}=1-x$   

b) $\sqrt{3x^2-13x+14}=x-3$

Phương pháp giải:

Bước 1: Bình phương hai vế và giải phương trình nhận được

Bước 2: Thử lại các giá trị x tìm được ở câu a có thỏa mãn phương trình đã cho hay không và kết luân nghiệm

Lời giải:

a) $\sqrt{2x^2+x+3}=1-x$

Bình phương hai vế của phương trình ta được:

$2x^2+x+3=1-2x+x^2$

Sau khi thu gọn ta được $x^2+3x+2=0$. Từ đó x=-1 hoặc x=-2

Thay lần lượt hai giá trị này của x vào phương trình đã cho ta thấy cả hai giá trị $x=-1;x=-2$ đều thỏa mãn

Vậy phương trình có tập nghiệm $S=\left\{-1;-2\right\}$

b) $\sqrt{3x^2-13x+14}=x-3$

Bình phương hai vế của phương trình ta được:
$3x^2-13x+14=x^2-6x+9$

Sau khi thu gọn ta được $2x^2-7x+5=0$. Từ đó $x=1$ hoặc $x=\frac{5}{2}$

Thay lần lượt hai giá trị này của x vào phương trình đã cho ta thấy không có giá trị nào của x thỏa mãn

Vậy phương trình vô nghiệm

Vận dụng trang 26 SGK Toán 10 Tập 2: Bác Việt sống và làm việc tại trạm hải đăng cách bờ biển 4km. Hằng tuần bác chèo thuyền vào vị trí gần nhất trên bờ biển là bến Bính để nhận hàng hóa do cơ quan cung cấp. Tuần này, do trục trặc về vận chuyển nên toàn bộ số hàng vẫn đang nằm ở Thôn Hoành, bên bờ biển cách bến Bính 9,25 km và sẽ được anh Nam vận chuyển trên con đường dọc bờ biển tới bến Bính bằng xe kéo. Bác Việt đã gọi điện thống nhất với anh Nam là họ sẽ gặp nhau ở vị trí nào đó giữa bến Bính và thôn Hoành để hai người có mặt tại đó cùng lúc, không mất thời gian cờ nhau. Tìm vị trí hai người dự định gặp nhau, biết rằng vận tốc kéo xe của anh Nam là 5 km/h và thuyền của bác Việt di chuyển với vân tốc 4 km/h. Ngoài ra giả thiết rằng đường bờ biển từ thôn Hoành đến bến Bính là đường thẳng và bác Việt cũng chèo thuyền tới một điểm trên bờ biền theo một đường thẳng.

Phương pháp giải:

Để hai người không phải chờ nhau thì thời gian chèo thuyền bằng thời gian kéo xe => lập phương trình.

Giải phương trình này sẽ tìm được vị trí hai người dự định gặp nhau.

Lời giải:

Giả sử bác Việt chèo thuyền cập bến ở vị trí M và ta đặt BM=x (km) (x>0)

Ta có: MC=BC-BM=9,25-x (km)

Thời gian di chuyển của anh Nam đến điểm hẹn gặp nhau là $\frac{9,25-x}{5}$$$(giờ)

Tam giác ABM vuông tại B, nên ta có:

$$$A{M}^2=A{B}^2+B{M}^2=x^2+16$

=> $AM=\sqrt{x^2+16}$ (km)

Thời gian di chuyển của bác Việt đến điểm hẹn găp nhau là: $\frac{\sqrt{x^2+16}}{4}$ (giờ)

Để hai người không phải chờ nhau thì ta có phương trình:

$\frac{\sqrt{x^2+16}}{4}=\frac{9,25-x}{5}$$\iff 5\sqrt{x^2+16}=37-4x$

Bình phương hai vế của phương trình trên ta được:

$25(x^2+16)=16x^2-296x+1369$

$\iff 9x^2+296x-969=0$

$\iff x=3$ hoặc $x=-\frac{323}{9}$

Thử lại ta thấy cả hai giá trị của x đều thỏa mãn

Mà x>0 nên ta chọn x=3

Vậy vị trí hai người gặp nhau cách bến Bính 3km và cách thôn Hoành 6,25 km

Bài tập

Câu hỏi trang 27 Toán 10

Bài 6.20 trang 27 SGK Toán 10 Tập 2: Giải các phương trình sau:

a) $\sqrt{3x^2-4x-1}=\sqrt{2x^2-4x+3}$

b) $\sqrt{x^2+2x-3}=\sqrt{-2x^2+5}$

c) $\sqrt{2x^2+3x-3}=\sqrt{-x^2-x+1}$ 

d) $\sqrt{-x^2+5x-4}=\sqrt{-2x^2+4x+2}$

Phương pháp giải:

Bước 1: Bình phương hai vế và giải phương trình nhận được

Bước 2: Thử lại các giá trị x nhận được ở trên có thỏa mãn phương trình đã cho hay không kết luận nghiệm

Lời giải:

a) $\sqrt{3x^2-4x-1}=\sqrt{2x^2-4x+3}$

Bình phương hai vế của phương trình ta được:

$\begin{array}{l}3x^2-4x-1=2x^2-4x+3\\ \iff x^2=4\end{array}$

$\iff x=2$ hoặc $x=-2$

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy cả 2 giá trị x=2; x=-2 thỏa mãn

Vậy tập nghiệm của phương trình là $S=\left\{-2;2\right\}$

b) $\sqrt{x^2+2x-3}=\sqrt{-2x^2+5}$

Bình phương hai vế của phương trình ta được:

$\begin{array}{l}{x}^2+2x-3=-2x^2+5\\ \iff 3x^2+2x-8=0\end{array}$

$\iff x=-2$ hoặc $x=\frac{4}{3}$

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy chỉ có giá trị $x=\frac{4}{3}$ thỏa mãn

Vậy tập nghiệm của phương trình là $x=\frac{4}{3}$

c) $\sqrt{2x^2+3x-3}=\sqrt{-x^2-x+1}$

Bình phương hai vế của phương trình ta được:

$\begin{array}{l}2x^2+3x-3=-x^2-x+1\\ \iff 3x^2+4x-4\end{array}$

$\iff x=-2$ hoặc $x=\frac{2}{3}$

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy cả 2 giá trị đều không thỏa mãn.

Vậy phương trình vô nghiệm

d) $\sqrt{-x^2+5x-4}=\sqrt{-2x^2+4x+2}$

Bình phương hai vế của phương trình ta được:

$\begin{array}{l}-x^2+5x-4=-2x^2+4x+2\\ \iff x^2+x-6=0\end{array}$

$\iff x=-3$ hoặc $x=2$

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy x=2 thỏa mãn.

Vậy nghiệm của phương trình là x=2

Bài 6.21 trang 27 SGK Toán 10 Tập 2: Giải các phương trình sau:

b) $\sqrt{2x^2+5x+3}=-3-x$

c) $\sqrt{3x^2-17x+23}=x-3$ 

d) $\sqrt{-x^2+2x+4}=x-2$

Phương pháp giải:

Bước 1: Bình phương hai vế và giải phương trình nhận được

Bước 2: Thử lại các giá trị x tìm được ở câu a có thỏa mãn phương trình đã cho hay không và kết luân nghiệm

Lời giải:

a) $\sqrt{6x^2+13x+13}=2x+4$    

Bình phương hai vế của phương trình ta được:

$\begin{array}{l}6x^2+13x+13=4x^2+16x+16\\ \iff 2x^2-3x-3=0\end{array}$

$\iff x=\frac{3-\sqrt{33}}{4}$ hoặc $x=\frac{3+\sqrt{33}}{4}$

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy cả 2 giá trị $x=\frac{3-\sqrt{33}}{4}$ và $x=\frac{3+\sqrt{33}}{4}$ đều thỏa mãn

Vậy tập nghiệm của phương trình là $S=\left\{\frac{3-\sqrt{33}}{4};\frac{3+\sqrt{33}}{4}\right\}$

b) $\sqrt{2x^2+5x+3}=-3-x$

Bình phương hai vế của phương trình ta được:

$\begin{array}{l}2x^2+5x+3=9+6x+x^2\\ \iff x^2-x-6=0\end{array}$

$\iff x=-2$ hoặc $x=3$

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy không có giá trị nào thỏa mãn

Vậy phương trình vô nghiệm

c) $\sqrt{3x^2-17x+23}=x-3$

Bình phương hai vế của phương trình ta được:

$\begin{array}{l}3x^2-17x+23=x^2-6x+9\\ \iff 2x^2-11x+14=0\end{array}$

$\iff x=2$ hoặc $x=\frac{7}{2}$

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy $x=\frac{7}{2}$ thỏa mãn

Vậy nghiệm của phương trình là $x=\frac{7}{2}$                  

d) $\sqrt{-x^2+2x+4}=x-2$

Bình phương hai vế của phương trình ta được:

$\begin{array}{l}-x^2+2x+4=x^2-4x+4\\ \iff 2x^2-6x=0\end{array}$

$\iff x=0$ hoặc $x=3$

Thay lần lượt các giá trị này vào phương trình đã cho, ta thấy x=3 thỏa mãn

Vậy nghiệm của phương trình là x=3

Bài 6.22 trang 27 SGK Toán 10 Tập 2: Cho từ giác ABCD có $AB\mathrm{\perp }CD;AB=2;BC=13;CD=8;DA=5$ (H.6.21). Gọi H là giao điểm của AB và CD và đặt x=AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD

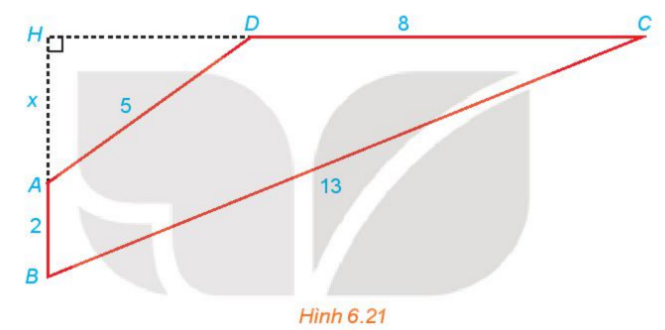
Phương pháp giải:

Bước 1: Tính HD,HC theo x

Bước 2: Sử dụng định lý py-ta-go cho tam giác vuông BHC

$B{C}^2=H{B}^2+H{C}^2$

Khi đó ta lập được phương trình $4\sqrt{25-x^2}=-x+19$

Bước 3: Giải phương trình trên ta tìm được x

Lời giải:

Ta có :AH=x (x>0)

Xét tam giác AHD vuông ở H, ta có:

$A{D}^2=A{H}^2+H{D}^2\iff H{D}^2=A{D}^2-A{H}^2=25-x^2$

$\Rightarrow HD=\sqrt{25-x^2}$

Ta có: $HC=HD+DC=\sqrt{25-x^2}+8$

$HB=AH+AB=x+2$

Xét tam giác HBC vuông tại H, ta có:

$\begin{array}{l}B{C}^2=H{B}^2+H{C}^2\\ \iff {13}^2=(x+2{)}^2+{\left(\sqrt{25-x^2}+8\right)}^2\\ \iff 169=x^2+4x+4+25-x^2+16\sqrt{25-x^2}+64\\ \iff 16\sqrt{25-x^2}=-4x+76\\ \iff 4\sqrt{25-x^2}=-x+19\end{array}$

Bình phương hai vế của phương trình trên ta được:

$\begin{array}{l}16(25-x^2)=x^2-38x+361\\ \iff 17x^2-38x-39=0\end{array}$

$\iff x=3$ hoặc $x=\frac{-13}{17}$

Thay lần lượt các giá trị trên vào phương trình, ta thấy hai giá trị đều thỏa mãn

Do x>0 nên ta chọn x=3 => AH=3

$\begin{array}{l}HD=\sqrt{25-3^2}=4\\ HC=4+8=12\\ HB=3+2=5\end{array}$

Diện tích tam giác HAD là $S_1=\frac{1}{2}.HA.HD=\frac{1}{2}.3.4=6$

Diện tích tam giác HBC là $S_2=\frac{1}{2}.HB.HC=\frac{1}{2}.5.12=30$

Vậy diện tích tứ giác ABCD là $S=S_2-S_1=30-6=24$

Bài 6.23 trang 27 SGK Toán 10 Tập 2: Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường. Minh đứng tại vị trí A cách lề đường một khoảng 50 m để chờ Hùng. Khi nhìn thấy Hùng đạp xe đến địa điểm B. cách mình một đoạn 200m thì Minh bắt đầu đi bộ ra lề đường để bắt kịp xe. Vận tốc đi bộ của Minh là 5 km/h, vận tốc xe đạp của Hùng là 15 km/h. Hãy xác định vị trí C trên lề đường (H.6.22) để hai bằng gặp nhau mà không bạn nào phải chờ người kia (làm tròn kết quả đến hàng phần mười)

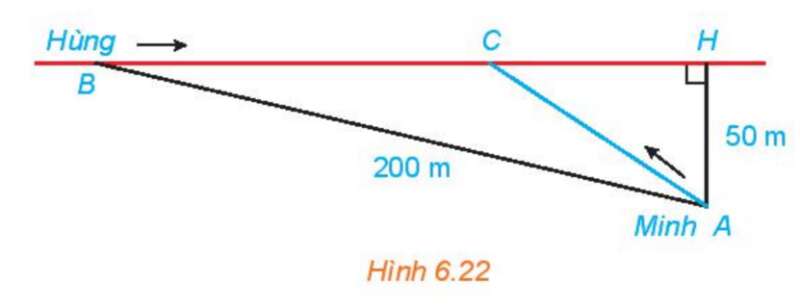
Phương pháp giải:

Bước 1: Đặt CH=x (km) (x>0)

Bước 2: Tính quãng đường Minh di chuyển, Hùng di chuyển

Bước 3: Để hai người không phải chờ nhau thì thời gian đi của 2 bạn phải bằng nhau nên ta lập được phương trình:

$\frac{\sqrt{0,0025+x^2}}{5}=\frac{\sqrt{15}-20x}{300}$

Giải phương trình tìm được x là tìm được vị trí điểm C

Lời giải:

Đổi: 200m=0,2 km

50m=0,05km

Đặt CH=x (km) (x>0)

Xét tam giác CHA vuông ở H, ta có:

$C{A}^2=C{H}^2+A{H}^2=x^2+0,0025$

=> Quãng đường Minh di chuyển là $CA=\sqrt{x^2+0,0025}$

Vận tốc đi bộ của Minh là 5km/h nên thời gian di chuyển của Minh là:

$\frac{\sqrt{x^2+0,0025}}{5}$ (giờ)

Xét tam giác AHB xuông tại H, ta có:

$\begin{array}{l}H{B}^2=A{B}^2-A{H}^2=(0,2{)}^2-(0,05{)}^2=0,0375\\ \Rightarrow HB=\frac{\sqrt{15}}{20}\end{array}$

=> Quãng đường mà Hùng di chuyển là: $BC=HB-HC=\frac{\sqrt{15}}{20}-x$

Vận tốc đạp xe của Hùng là 15km/h nên thời gian di chuyển của Hùng là:

$\frac{\frac{\sqrt{15}}{20}-x}{15}=\frac{\sqrt{15}-20x}{300}$ (giờ)

Để hai bạn không phải chờ nhau thì:

$\begin{array}{l}\frac{\sqrt{x^2+0,0025}}{5}=\frac{\sqrt{15}-20x}{300}\\ \iff 60\sqrt{x^2+0,0025}=\sqrt{15}-20x\end{array}$

Bình phương hai vế của phương trình trên ta được:

$\begin{array}{l}3600\left(x^2+0,0025\right)=15-40\sqrt{15}x+400x^2\\ \iff 3200x^2+40\sqrt{15}x-6=0\end{array}$

$\iff x=\frac{-\sqrt{15}-3\sqrt{7}}{160}$ hoặc $x=\frac{-\sqrt{15}+3\sqrt{7}}{160}$

Thay lần lượt các giá trị này vào phương trình đầu, ta thấy cả 2 giá trị đều thỏa mãn

Do x>0 nên ta chọn $x=\frac{-\sqrt{15}+3\sqrt{7}}{160}$

$\Rightarrow BC=BH-CH=\frac{\sqrt{15}}{20}-\frac{-\sqrt{15}+3\sqrt{7}}{160}\approx 0,1682(km)=168,2(m)$

Vậy vị trí C thỏa mãn đề bài là điểm cách B khoảng 168,2 m