Giải Toán 11 trang 11 Tập 1 (Kết nối tri thức)

Ngọc Nguyễn Ngày: 03-02-2024 Lớp 11

290

Với giải SGK Toán 11 Kết nối tri thức trang 11 chi tiết trong Bài 1: Giá trị lượng giác của góc lượng giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 trang 11 Tập 1 (Kết nối tri thức)

Luyện tập 4 trang 11 Toán 11 Tập 1: Xác định các điểm M và N trên đường tròn lượng giác lần lượt biểu diễn các góc lượng giác có số đo bằng $- \frac{15 π}{4}$ và 420°.

Lời giải:

Ta có: $- \frac{15 π}{4} = - (\frac{3 π}{4} + 3 π)$ , điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng $- \frac{15 π}{4}$ được xác định trong hình dưới đây:

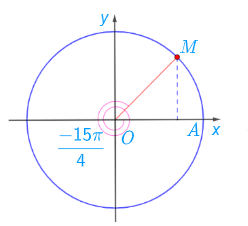
Toán 11 Bài 1 (Kết nối tri thức): Giá trị lượng giác của góc lượng giác (ảnh 8)

Ta có: 420° = 60° + 360°, điểm N trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng 420° được xác định trong hình dưới đây:

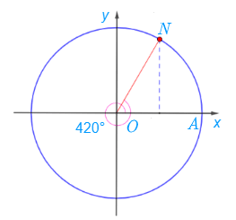
Toán 11 Bài 1 (Kết nối tri thức): Giá trị lượng giác của góc lượng giác (ảnh 9)

HĐ5 trang 11 Toán 11 Tập 1: Nhắc lại khái niệm các giá trị lượng giác sin α, cos α, tan α, cot α của góc α (0° ≤ α ≤ 180°) đã học ở lớp 10 (H.1.9a).

Toán 11 Bài 1 (Kết nối tri thức): Giá trị lượng giác của góc lượng giác (ảnh 10)

Lời giải:

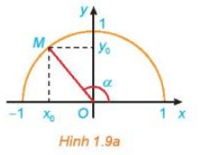
Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x₀; y₀) là điểm trên nửa đường tròn đơn vị sao cho $\hat{x O M} = α$ . Khi đó:

• sin của góc α là tung độ y₀ của điểm M, kí hiệu là sin α

sin α = y₀.

• côsin của góc α là hoành độ của x₀ của điểm M, kí hiệu là cos α

cos α = x₀.

• Khi α ≠ 90° (hay là x₀ ≠ 0), tang của α là $\frac{y_{0}}{x_{0}}$ , kí hiệu là tan α

$\tan α = \frac{\sin α}{\cos α} = \frac{y_{0}}{x_{0}}$ .

• Khi α ≠ 0° và α ≠ 180° (hay là y₀ ≠ 0), côtang của α là $\frac{x_{0}}{y_{0}}$ , kí hiệu là cot α.

$\cot α = \frac{\cos α}{\sin α} = \frac{x_{0}}{y_{0}}$ .

Luyện tập 5 trang 12 Toán 11 Tập 1: Cho góc lượng giác có số đo bằng $\frac{5 π}{6}$ .

a) Xác định điểm M trên đường tròn lượng giác biểu diễn góc lượng giác đã cho.

b) Tính các giá trị lượng giác của góc lượng giác đã cho.

Lời giải:

a) Điểm M trên đường tròn lượng giác biểu diễn góc lượng giác có số đo bằng $\frac{5 π}{6}$ được xác định trong hình sau:

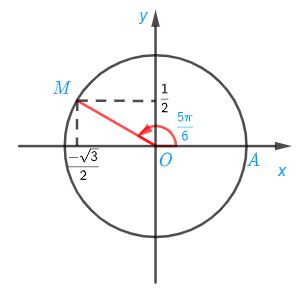
Toán 11 Bài 1 (Kết nối tri thức): Giá trị lượng giác của góc lượng giác (ảnh 11)

b) Ta có:

$\cos \frac{5 π}{6} = - \frac{\sqrt{3}}{2}; \sin \frac{5 π}{6} = \frac{1}{2}$ ;

$\tan \frac{5 π}{6} = \frac{\sin \frac{5 π}{6}}{\cos \frac{5 π}{6}} = - \frac{\sqrt{3}}{3}; \cot \frac{5 π}{6} = \frac{\cos \frac{5 π}{6}}{\sin \frac{5 π}{6}} = - \sqrt{3}$ .