Bài 1.2 trang 7 SBT Toán 11 Tập 1: Trên đường tròn lượng giác, xác định điểm Q biểu diễn các góc lượng giác có số đo sau:

a) $\frac{\pi }{6}$ ;                     b) $\frac{-5\pi }{7}$ ;

c) 270°;                         d) – 415°.

Lời giải:

a) Điểm Q trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là $\frac{\pi }{6}$  được xác định như hình dưới đây.

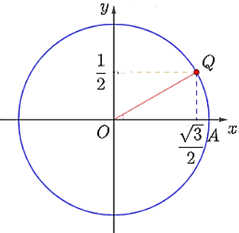
b) Điểm Q trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là $\frac{-5\pi }{7}$  được xác định như hình dưới đây.

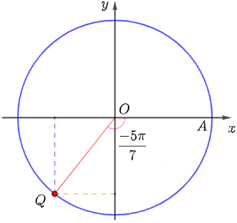
c) Điểm Q trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là 270° được xác định như hình dưới đây.

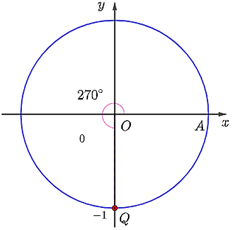
d) Điểm Q trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là – 415° được xác định như hình dưới đây.

Bài 1.3 trang 7 SBT Toán 11 Tập 1: Một đường tròn có bán kính 20 m. Tìm độ dài của cung trên đường tròn đó có số đo là:

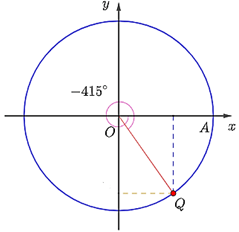
a) $\frac{2\pi }{7}$ ;                  b) 36°. 

Lời giải:

a) Ta có l = Rα = 20 . $\frac{2\pi }{7}=\frac{40\pi }{7}$  (m).

b) Ta có l = R . $\frac{\pi a}{180}=20.\frac{\pi .36}{180}=4\pi$  (m).

Bài 1.4 trang 7 SBT Toán 11 Tập 1: Cho cos x = $-\frac{5}{13}$  (90° < x < 180°). Tính các giá trị lượng giác còn lại của góc x.

Lời giải:

Từ đẳng thức sin² x + cos² x = 1, suy ra

sin² x = 1 – cos² x = $1-{\left(-\frac{5}{13}\right)}^2=\frac{144}{169}$

Mặt khác 90° < x < 180° nên sinx > 0. Do đó sin x = $\sqrt{\frac{144}{169}}=\frac{12}{13}$ .

Suy ra tan x = $\frac{\sin x}{\cos x}=\frac{12}{13}:\left(-\frac{5}{13}\right)=-\frac{12}{5}$ , cot x = $\frac{\cos x}{\sin x}=\left(-\frac{5}{13}\right):\frac{12}{13}=-\frac{5}{12}$ .

Bài 1.5 trang 7 SBT Toán 11 Tập 1: Cho sin a + cos a = m. Hãy tính theo m.

a) sin a cos a;

b) sin³ a + cos³ a;

c) sin⁴ a + cos⁴ a.

Lời giải:

a) Ta có: sin a + cos a = m nên (sin a + cos a)² = m²

hay sin² a + cos² a + 2sin a cos a = m² hay 1 + 2sin a cos a = m².

Từ đó suy ra sin a cos a = $\frac{m^2-1}{2}$ .

b) sin³ a + cos³ a = (sin a + cos a)³ – 3sin a cos a(sin a + cos a)

= m³ – 3m $\frac{m^2-1}{2}=\frac{3m-m^3}{2}$.  

c) sin⁴ a + cos⁴ a = (sin² a + cos² a)² – 2sin² a cos² a

= 1 – 2(sin a cos a)² = $1-2.{\left(\frac{m^2-1}{2}\right)}^2=1-\frac{{\left(m^2-1\right)}^2}{2}$ .

Bài 1.6 trang 7 SBT Toán 11 Tập 1: Chứng minh các đẳng thức sau:

a) cos⁴ x – sin⁴ x = 2 cos² x – 1;

b) tan² x – sin² x = tan² x . sin² x;

c) (sin x + cos x)² + (sin x – cos x)² = 2.     

Lời giải:

a) Ta có VT = cos⁴ x – sin⁴ x

= (cos² x – sin² x)(cos² x + sin² x)

= cos² x – sin² x

= cos² x – (1 – cos² x) = 2 cos² x – 1 = VP.                   

b) Ta có

VT = tan² x – sin² x = $\frac{{\sin }^{2}x}{{\cos }^{2}x}-{\sin }^{2}x$$=\frac{{\sin }^{2}x-{\sin }^{2}x{\cos }^{2}x}{{\cos }^{2}x}$$=\frac{{\sin }^{2}x\left(1-{\cos }^{2}x\right)}{{\cos }^{2}x}$

$=\frac{{\sin }^{2}x}{{\cos }^{2}x}.{\sin }^{2}x$ = tan² x . sin² x = VP.                    

c) Ta có

VT = (sin x + cos x)² + (sin x – cos x)²

= sin² x + 2sin x cos x + cos² x + sin² x – 2sin x cos x + cos² x

= 2 sin² x + 2 cos² x = 2(sin² x + cos² x) = 2 . 1 = 2 = VP.

SBT Toán 11 Kết nối tri thức trang 9

Bài 1.7 trang 9 SBT Toán 11 Tập 1: Rút gọn biểu thức

A = 2cos⁴ x – sin⁴ x + sin² x cos² x + 3 sin² x.

Lời giải:

A = 2cos⁴ x – sin⁴ x + sin² x cos² x + 3 sin² x

= cos⁴ x – sin⁴ x + cos⁴ x + sin² x cos² x + 3 sin² x

= (cos² x – sin² x)(cos² x + sin² x) + cos² x (cos² x + sin² x) + 3sin² x

= cos² x – sin² x + cos² x + 3 sin² x

= 2cos² x + 2 sin² x

= 2(cos² x + sin² x)

= 2 . 1 = 2.

Bài 1.8 trang 9 SBT Toán 11 Tập 1: Bánh xe của người đi xe đạp quay được 12 vòng trong 6 giây.

a) Tính góc (theo độ và rađian) mà bánh xe quay được trong 1 giây.

b) Tính quãng đường mà người đi xe đạp đã đi được trong 1 phút, biết rằng đường kính bánh xe đạp là 860 mm.

Lời giải:

a) Trong 1 giây, bánh xe quay được $\frac{12}{6}$  = 2 vòng, tức là quay được một góc 4π (rad) hay 720°.

b) Bán kính xe đạp là: 860 : 2 = 430 (mm).

Trong 1 phút, quãng đường mà người đi xe đã đi được là:

l = 430 . 4π . 60 = 103 200π (mm).

Bài 1.9 trang 9 SBT Toán 11 Tập 1: Kim giờ dài 6 cm và kim phút dài 11 cm của đồng hồ chỉ 4 giờ. Hỏi thời gian ít nhất để 2 kim vuông góc với nhau là bao nhiêu? Lúc đó tổng quãng đường hai đầu mút kim giờ và kim phút đi được là bao nhiêu?

Lời giải:

Một giờ, kim phút quét được một góc lượng giác 2π; kim giờ quét được một góc $\frac{\pi }{6}$ .

Hiệu vận tốc giữa kim phút và kim giờ là $2\pi -\frac{\pi }{6}=\frac{11\pi }{6}$ .

Vào lúc 4 giờ hai kim tạo với nhau một góc là $\frac{2\pi }{3}$ .

Khoảng thời gian ít nhất để hai kim vuông góc với nhau là

$\left(\frac{2\pi }{3}-\frac{\pi }{2}\right):\frac{11\pi }{6}=\frac{1}{11}$ (giờ).

Vậy sau $\frac{1}{11}$  (giờ) hai kim sẽ vuông góc với nhau.

Tổng quãng đường hai đầu mút kim đi được là

l = R .α = $6.\frac{1}{11}.\frac{\pi }{6}+11.\frac{1}{11}.2\pi =\frac{23\pi }{11}$ (cm).

Xem thêm các bài SBT Toán 11 Kết nối tri thức hay, chi tiết khác:

Bài 2: Công thức lượng giác

Bài 3: Hàm số lượng giác

Bài 4: Phương trình lượng giác cơ bản

Bài tập cuối chương 1 trang 25

Bài 5: Dãy số