Giải Toán 11 trang 16 Tập 1 (Chân trời sáng tạo)

Giải Toán 11 trang 16 Tập 1 (Chân trời sáng tạo)

Ngọc Nguyễn Ngày: 07-04-2023 Lớp 11

290

Với giải SGK Toán 11 Chân trời sáng tạo trang 16 chi tiết trong Bài 2: Giá trị lượng giác của một góc lượng giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 trang 16 Tập 1 (Chân trời sáng tạo)

Thực hành 1 trang 15 Toán 11 Tập 1: Tính sin $(- \frac{2 π}{3})$ và tan495°.

Lời giải:

Ta có: sin $(- \frac{2 π}{3})$ = -sin $(\frac{2 π}{3})$ = $- \frac{\sqrt{3}}{2}$ .

Ta có tan495° = – tan135° = – tan45° = $- \frac{cos 45 °}{\sin 45 °}$ = -1.

Thực hành 2 trang 16 Toán 11 Tập 1: Sử dụng máy tính cầm tay để tính cos75° và tan $(\frac{- 19 π}{6})$ .

Lời giải:

Sử dụng máy tính cầm tay ta tính được:

cos75° = $\frac{\sqrt{6} - \sqrt{2}}{4}$ ;

tan $(\frac{- 19 π}{6}) = - \frac{\sqrt{3}}{3}$ .

Hoạt động khám phá 2 trang 16 Toán 11 Tập 1: a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác. Giải thích vì sao sin²α + cos²α = 1.

b) Chia cả hai vễ của biểu thức ở câu a) cho cos²α ta được đẳng thức nào?

c) Chia cả hai vế của biểu thức ở câu a) cho sin²α ta được đẳng thức nào?

Lời giải:

a) M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác nên tọa độ điểm M là (cosα; sinα) nên MH = sinα, OH = cosα.

Ta lại có: MH² + OH² = 1 (định lí Pythagore)

Hay sin²α + cos²α = 1.

b) Vì OH = cosα > 0 nên cos²α ≠ 0 nên chia cả hai vế của biểu thức của câu a) cho cos²α, ta được:

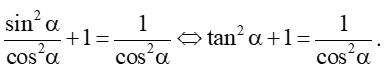
Toán 11 Bài 2 (Chân trời sáng tạo): Giá trị lượng giác của một góc lượng giác (ảnh 2)

c) Vì MH = sinα > 0 nên sin²α ≠ 0 nên chia cả hai vế của biểu thức của câu a) cho sin²α, ta được:

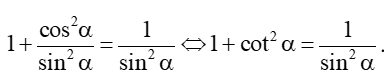
Toán 11 Bài 2 (Chân trời sáng tạo): Giá trị lượng giác của một góc lượng giác (ảnh 3)

Xem thêm các bài giải Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Hoạt động khởi động trang 13 Toán 11 Tập 1: Hình bên biểu diễn xích đu IA có độ dài 2m dao động quanh trục IO vuông góc với trục Ox trên mặt đất và A’ là hình chiếu của A lên Ox. Tọa độ s của A’ trên trục Ox được gọi là li độ của A và (IO, IA) = α được gọi là li độ góc của A. Làm cách nào để tính li độ dựa vào li độ góc?

Hoạt động khám phá 1 trang 13 Toán 11 Tập 1: Trong Hình 1, M và N là điểm biểu diễn của các góc lượng giác và trên đường tròn lượng giác. Xác định tọa độ của M và N trong hệ trục tọa độ Oxy.

Thực hành 1 trang 15 Toán 11 Tập 1: Tính sin $(- \frac{2 π}{3})$ và tan495°.

Thực hành 2 trang 16 Toán 11 Tập 1: Sử dụng máy tính cầm tay để tính cos75° và tan $(\frac{- 19 π}{6})$ .

Hoạt động khám phá 2 trang 16 Toán 11 Tập 1: a) Trong Hình 5, M là điểm biểu diễn của góc lượng giác α trên đường tròn lượng giác. Giải thích vì sao sin²α + cos²α = 1.

Hoạt động khám phá 3 trang 17 Toán 11 Tập 1: Cho . Biểu diễn các góc lượng giác – α, α + π, π – α, trên đường tròn lượng giác và rút ra mối liên hệ giữa giá trị lượng giác của các góc này với giá trị lượng giác của góc α.

Thực hành 4 trang 19 Toán 11 Tập 1: a) Biểu diễn cos638° qua giá trị lượng giác của góc có số đo từ 0° đến 45°.

Vận dụng trang 19 Toán 11 Tập 1: Trong Hình 11, vị trí cabin mà Bình và Cường ngồi trên vòng quay được đánh dấu bởi điểm B và C.

Bài 1 trang 19 Toán 11 Tập 1: Các đẳng thức sau có thể đồng thời xảy ra không?

Bài 2 trang 19 Toán 11 Tập 1: Cho sinα = $\frac{12}{13}$ và cosα = $- \frac{5}{13}$ . Tính $\sin (- \frac{15 π}{2} - α) - cos (13 π + α)$ .

Bài 3 trang 19 Toán 11 Tập 1: Tính các giá trị lượng giác của góc α, nếu: a) sin $α$ = $\frac{5}{13}$ và $\frac{π}{2} < α < π$ ;

Bài 4 trang 19 Toán 11 Tập 1: Biểu diễn các giá trị lượng giác sau qua các giá trị lượng giác của góc có số đo từ 0 đến $\frac{π}{4}$ hoặc từ 0 đến 45° và tính: a) cos $\frac{21 π}{6}$ ;

Bài 5 trang 19 Toán 11 Tập 1: Chứng minh đẳng thức lượng giác sau: a) sin⁴α – cos⁴α = 1 – 2cos²α;

Bài 6 trang 19 Toán 11 Tập 1: Rút gọn các biểu thức sau:

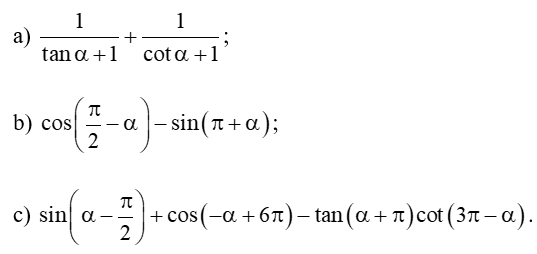
Toán 11 Bài 2 (Chân trời sáng tạo): Giá trị lượng giác của một góc lượng giác (ảnh 18)

Bài 7 trang 20 Toán 11 Tập 1:Thanh OM quay ngược chiều kim đồng hồ quanh trục O của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là OA. Hỏi độ dài bóng O’M’ của OM khi thanh quay được vòng là bao nhiêu, biết độ dài thanh OM là 15 cm? Kết quả làm tròn đến hàng phần mười.

Bài 8 trang 20 Toán 11 Tập 1: Khi đạp xe di chuyển, van V của bánh xe quay quanh trục O theo chiều kim đồng hồ với tốc độ góc không đổi là 11 rad/s (Hình 13). Ban đầu van nằm ở vị trí A. Hỏi sau một phút di chuyển , khoảng cách từ van đến mặt đất là bao nhiêu, biết bán kính OA = 58 cm? Giả sử độ dàu của lốp xe không đáng kể. Kết quả làm tròn đến hàng phần mười.

Xem thêm lời giải sách giáo khoa Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Góc lượng giác

Bài 3: Các công thức lượng giác

Bài 4: Hàm số lượng giác và đồ thị

Bài 5: Phương trình lượng giác

Bài tập cuối chương 1

Từ khóa :

Giải bài tập Toán 11

Đánh giá

0

0 đánh giá

Đánh giá

Bài viết cùng môn học

Toán Lớp 6

Toán 6 ( Kết nối tri thức): Luyện tập chung

Toán 6 ( Kết nối tri thức): Luyện tập chung Mai Hương

224

Toán Lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.16 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

261

Toán Lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.15 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

282

Toán Lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6

Bài 5.14 trang 109 Toán 6 Tập 1 | Kết nối tri thức Giải Toán lớp 6 Mai Hương

233

Tìm kiếm

Bài Viết Xem Nhiều

Bài Viết Cùng Lớp

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK

- Người đại diện: Nguyễn Thanh Tuyền

- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.

2021 © All Rights Reserved.