Với giải SGK Toán 11 Chân trời sáng tạo trang 19 chi tiết trong Bài 2: Giá trị lượng giác của một góc lượng giác giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:
Giải Toán 11 trang 19 Tập 1 (Chân trời sáng tạo)
b) Biểu diễn cot qua giá trị lượng giác của góc có số đo từ 0 đến .
Lời giải:
a) Ta có: cos638° = cos(2.360° + (– 82°)) = cos(– 82°) = cos82° = cos(90° – 8°) = sin8°.
b) Ta có: .
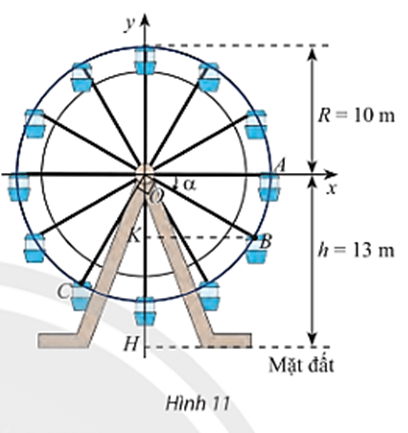
a) Chứng minh rằng chiều cao từ điểm B đến mặt đất bằng (13 + 10sinα) mét với α là số đo của một góc lượng giác tia đầu OA, tia cuối OB. Tính độ cao của điểm B so với mặt đất khi α = – 30°.
b) Khi điểm B cách mặt đất 4m thì điểm C cách mặt đất bao nhiêu mét? Làm tròn kết quả đến hàng phần trăm.
Lời giải:
a) Ta có điểm B là điểm biểu diễn cho góc lượng giác có số đo góc là α trên đường tròn lượng giác có bán kính bằng 10 nên tọa độ điểm B(10cosα; 10sinα).
Vì vậy chiều cao từ điểm B đến mặt đất là: 13 + 10sinα (mét).
Với α = – 30° ta có chiều cao từ điểm B đến mặt đất là: 13 + 10sin.(– 30°) = 8 (mét).
b) Đặt (OA, OC) = β = α – 90°
Nếu điểm B cách mặt đất 4m thì 13 + 10sinα = 4
⇔ sinα =
Ta có sinα = cos(α – 90°) =
⇒ cos(α – 90°) =
⇒ cosβ =
⇒ sinβ =
Vì vậy chiều cao từ điểm C đến mặt đất là: 13 + 10sinβ = 13 + 10. ≈ 8,64 (mét).
Bài tập
Bài 1 trang 19 Toán 11 Tập 1: Các đẳng thức sau có thể đồng thời xảy ra không?
a) sinα = và cosα = ;
b) sinα = và cotα = ;
c) tanα = 3 và cotα = .
Lời giải:
a) Với – 1 ≤ sinα = ≤ 1 và – 1 ≤ cosα = ≤ 1, ta có:
sin2α + cos2α = = 1.
Vậy sinα = và cosα = có thể đồng thời xảy ra.
b) Với – 1 ≤ sinα = ≤ 1 và cotα = , ta có:
1 + cot2α =
Do đó 1 + cot2α ≠ .
Vì vậy sinα = và cotα = không đồng thời xảy ra.
c) Với tanα = 3 và cotα = , ta có:
tanα . cotα = 3. = 1.
Vì vậy tanα = 3 và cotα = đồng thời xảy ra.
Bài 2 trang 19 Toán 11 Tập 1: Cho sinα = và cosα = . Tính .
Lời giải:
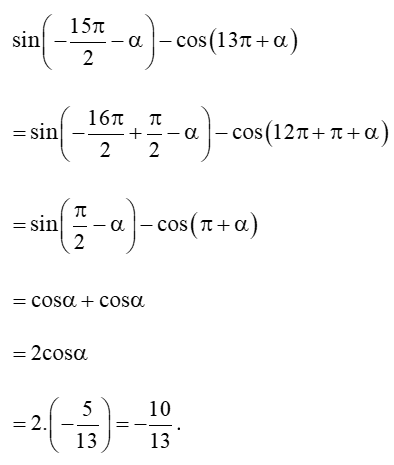
Bài 3 trang 19 Toán 11 Tập 1: Tính các giá trị lượng giác của góc α, nếu:
a) sin = và ;
b) cos = và ;
c) tan = và ;
d) cot = và .
Lời giải:
a) Ta có:
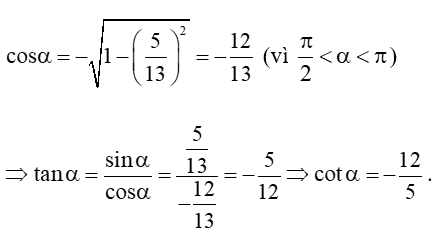
Vậy .
b) Ta có:
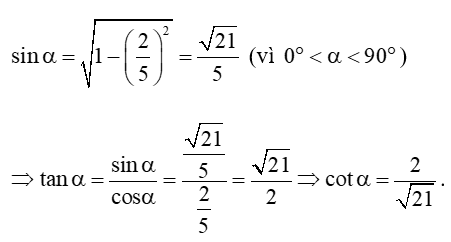
Vậy .
c) Ta có: tan = cot =
Ta lại có:
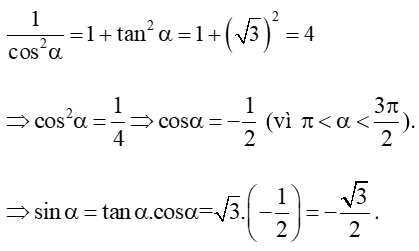
Vậy .
d) Ta có:
Ta lại có:
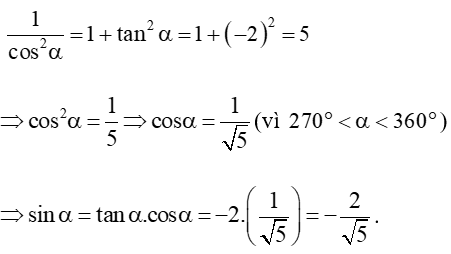
Vậy .
a) cos;
b) sin;
c) tan1 020°.
Lời giải:
a) Ta có: 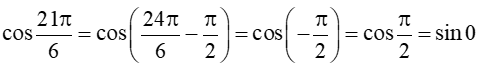 .
.
b) 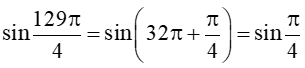 .
.
c) tan1 020° = tan(3.180° – 60°) = tan(180° – 60°) = – tan60° = – cot30°.
Bài 5 trang 19 Toán 11 Tập 1: Chứng minh đẳng thức lượng giác sau:
a) sin4α – cos4α = 1 – 2cos2α;
b) tanα + cotα = .
Lời giải:
a) Ta có: sin4α – cos4α = (sin2α – cos2α).(sin2α + cos2α ) = sin2α + cos2α – 2cos2α = 1 – 2cos2α.
b) Ta có: tanα + cotα =
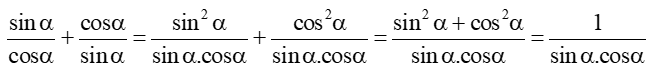
Bài 6 trang 19 Toán 11 Tập 1: Rút gọn các biểu thức sau:
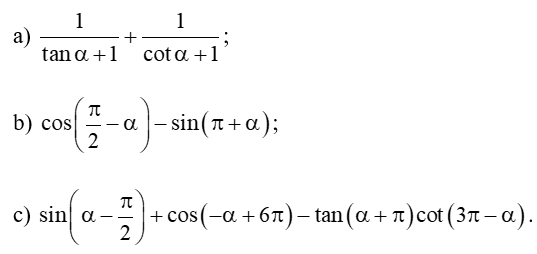
Lời giải:
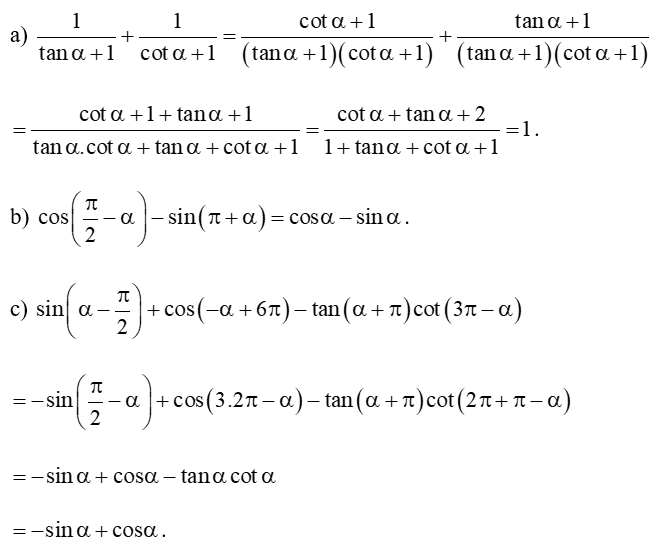
Xem thêm các bài giải Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Thực hành 1 trang 15 Toán 11 Tập 1: Tính sin và tan495°.
Thực hành 2 trang 16 Toán 11 Tập 1: Sử dụng máy tính cầm tay để tính cos75° và tan.
Bài 1 trang 19 Toán 11 Tập 1: Các đẳng thức sau có thể đồng thời xảy ra không?
Bài 2 trang 19 Toán 11 Tập 1: Cho sinα = và cosα = . Tính .
Bài 3 trang 19 Toán 11 Tập 1: Tính các giá trị lượng giác của góc α, nếu: a) sin = và ;
Bài 5 trang 19 Toán 11 Tập 1: Chứng minh đẳng thức lượng giác sau: a) sin4α – cos4α = 1 – 2cos2α;
Bài 6 trang 19 Toán 11 Tập 1: Rút gọn các biểu thức sau:
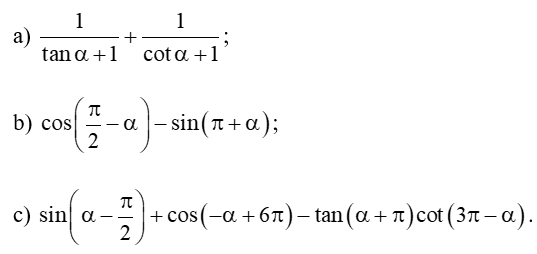
Xem thêm lời giải sách giáo khoa Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 3: Các công thức lượng giác
Bài 4: Hàm số lượng giác và đồ thị
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.