Với giải SGK Toán 11 Chân trời sáng tạo trang 42 chi tiết trong Bài tập cuối chương 1 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 11. Mời các bạn đón xem:

Giải Toán 11 trang 42 Tập 1 (Chân trời sáng tạo)

Bài 1 trang 42 Toán 11 Tập 1: Góc lượng giác nào tương ứng với chuyển động quay $3\frac{1}{5}$ vòng ngược chiều kim đồng hồ?

A. $\frac{16\pi }{5}$;

B. ${\left(\frac{16}{5}\right)}^o$

C. 1 152°;

D. 1 152π.

Lời giải:

Đáp án đúng là C

Mỗi vòng kim đồng hồ quay là: 2π nên góc lượng giác quét được khi quay $3\frac{1}{5}$ vòng là $3\frac{1}{5}.2\pi =3.2\pi +\frac{2\pi }{5}$ rad.

Khi đó điểm biểu diễn cho các góc lượng giác này có công thức số đo tổng quát là $\frac{2\pi }{5}+k2\pi ,k\in \mathbb{Z}$.

Xét 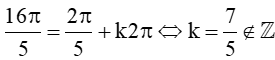. Do đó góc này không tương ứng với góc đã cho.

Xét 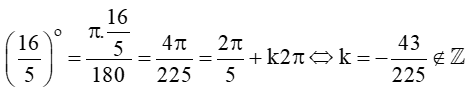. Do đó góc này không tương ứng với góc đã cho.

Xét 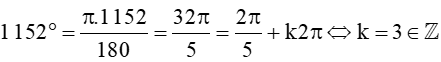. Do đó góc này tương ứng với góc đã cho.

Xét 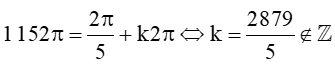. Do đó góc này không tương ứng với góc đã cho.

Bài 2 trang 42 Toán 11 Tập 1: Trong trường hợp nào dưới đây cosα = cosβ và sinα = – sinβ ?

A. β = – α;

B. β = π – α;

C. β = π + α;

D. $\beta =\frac{\pi }{2}+\alpha$.

Lời giải:

Đáp án đúng là: A

+) Xét β = – α, khi đó:

cosβ = cos(– α) = cosα;

sinβ = sin(– α) = sinα hay sinα = – sinβ .

Do đó A thỏa mãn.

+) Xét β = π – α, khi đó:

cosβ = cos(π – α) = – cosα;

sinβ = sin(π – α) = sinα.

Do đó B không thỏa mãn.

+) Xét β = π + α, khi đó:

cosβ = cos(π + α) = – cosα;

sinβ = sin(π + α) = – sinα.

Do đó C không thỏa mãn.

+) Xét $\beta =\frac{\pi }{2}+\alpha$, khi đó:

cosβ = cos($\frac{\pi }{2}+\alpha$) = – sinα;

sinβ = sin($\frac{\pi }{2}+\alpha$) = cosα.

Do đó D không thỏa mãn.

Bài 3 trang 42 Toán 11 Tập 1: Khẳng định nào sau đây đúng?

A. Hàm số y = sinx là hàm số chẵn;

B. Hàm số y = cosx là hàm số chẵn;

C. Hàm số y = tanx là hàm số chẵn;

D. Hàm số y = cotx là hàm số chẵn.

Lời giải:

Đáp án đúng là: B

Ta có tập xác định của hàm số y = cosx là ℝ.

Nếu với x ∈ ℝ thì – x ∈ ℝ và y(– x) = cos(– x) = cosx = y(x).

Vậy hàm số y = cosx là hàm số chẵn.

Bài 4 trang 42 Toán 11 Tập 1: Nghiệm âm lớn nhất của phương trình lượng giác cos2x = cos$\left(x+\frac{\pi }{3}\right)$ là

A. $-\frac{\pi }{9}$;

B. $-\frac{5\pi }{3}$;

C. $-\frac{7\pi }{9}$;

D. $-\frac{13\pi }{9}$.

Lời giải:

Đáp án đúng là: A

cos2x = cos$\left(x+\frac{\pi }{3}\right)$

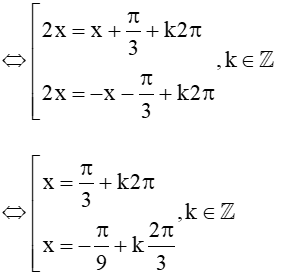
+) Với x = $\frac{\pi }{3}$ + k2$\pi$, k$\in$Z đạt giá trị âm lớn nhất khi k = – 1 và bằng: $\frac{\pi }{3}-2\pi =-\frac{5\pi }{3}$.

+) Với $x=-\frac{\pi }{9}+k\frac{2\pi }{3},k\in \mathbb{Z}$ đạt giá trị âm lớn nhất khi k = 0 và bằng: $-\frac{\pi }{9}+0.\frac{2\pi }{9}=-\frac{\pi }{9}$.

Vậy nghiệm âm lớn nhất của phương trình đã cho là $-\frac{\pi }{9}$.

Bài 5 trang 42 Toán 11 Tập 1: Số nghiệm của phương trình tanx = 3 trong khoảng $\left(-\frac{\pi }{2};\frac{7\pi }{3}\right)$ là

A. 1;

B. 2;

C. 3;

D. 4.

Lời giải:

Xét phương trình tanx = 3

⇔ x ≈ 1,25 + kπ, k ∈ ℤ

Xét: $-\frac{\pi }{2}<x<\frac{7\pi }{3}\iff -\frac{\pi }{2}<1,25+k\pi <\frac{7\pi }{3}\iff$ -0,9 < k < 1,94.

Mà k ∈ ℤ nên k ∈ {0; 1}.

Vậy có 2 nghiệm của phương trình đã cho nằm trong khoảng $\left(-\frac{\pi }{2};\frac{7\pi }{3}\right)$.

Bài 6 trang 42 Toán 11 Tập 1: Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức h(t) = 29 + 3sin$\frac{\pi }{12}$(t-9), với h được tính bằng độ C và t là thời gian trong ngày tính bằng giờ. Nhiệt độ thấp nhất trong ngày là bao nhiêu độ C và vào lúc mấy giờ

(Theo https://www.sciencedirect.com/science/article/abs/pii/0168192385900139)

A. 32°C, lúc 15 giờ;

B. 29°C, lúc 9 giờ;

C. 26°C, lúc 3 giờ;

D. 26°C, lúc 0 giờ

Lời giải:

Vì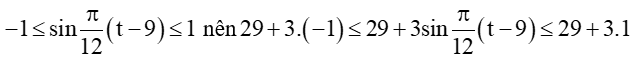 

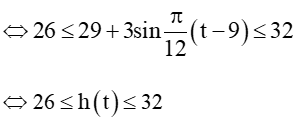
Nhiệt độ thấp nhất trong ngày là 26°C khi

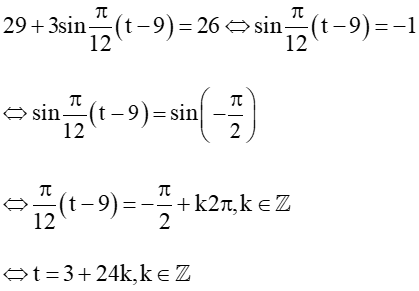
Vì vậy vào thời điểm 3 giờ trong ngày thì nhiều độ thấp nhất của thành phố là 26°C.

Bài 7 trang 42 Toán 11 Tập 1: Một chiếc quạt trần năm cánh quay với tốc độ 45 vòng trong một phút. Chọn chiều quay của quạt là chiều thuận. Sau 3 giây, quạt quay được một góc có số đo bao nhiêu radian?

Lời giải:

Tốc độ góc của quạt trần là: $\frac{45.2\pi }{60}=\frac{3\pi }{2}$(rad/s).

Sau 3 giây, quạt quay được một góc có số đo là: $\frac{3\pi }{2}.3=\frac{9\pi }{2}$rad.

Bài 8 trang 42 Toán 11 Tập 1: Cho cosα = $\frac{1}{3}$ và $-\frac{\pi }{2}<\alpha <0$. Tính:

a) sinα;

b) sin2α;

c) cos$\left(\alpha +\frac{\pi }{3}\right)$.

Lời giải:

a) sinα =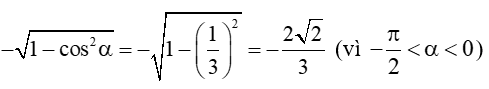 

b) sin2α = 2sinα.cosα = $2.\frac{1}{3}\left(-\frac{2\sqrt{2}}{3}\right)=-\frac{4\sqrt{2}}{9}$.

c)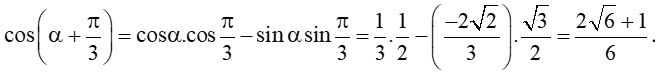 

Bài 9 trang 42 Toán 11 Tập 1: Chứng minh đẳng thức lượng giác:

a) sin(α + β)sin(α – β) = sin²α – sin²β;

b) cos⁴α – cos⁴$\left(\alpha -\frac{\pi }{2}\right)$ = cos2α.

Lời giải:

a) sin(α + β)sin(α – β) = sin²α – sin²β

Ta có: sin(α + β)sin(α – β) =

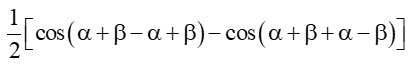
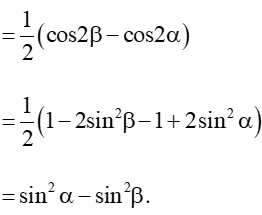
b) Ta có: cos⁴α – cos⁴$\left(\alpha -\frac{\pi }{2}\right)$ = cos⁴α – sin⁴α = (cos²α – sin²α)(cos²α + sin²α)

= cos²α – sin²α = cos2α.