Công thức biện luận số nghiệm của phương trình dựa vào đồ thị chi tiết

Giang Ngày: 07-06-2023 Lớp 12

346

Toptailieu.vn biên soạn và giới thiệu Công thức biện luận số nghiệm của phương trình dựa vào đồ thị hay, chi tiết, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về hàm số, từ đó học tốt môn Toán.

Công thức biện luận số nghiệm của phương trình dựa vào đồ thị chi tiết

1. Lí thuyết

Cho hai hàm số $y = f (x)$ có đồ thị $(C_{1})$ và $y = g (x)$ có đồ thị $(C_{2})$ . Khi đó số nghiệm của phương trình $f (x) = g (x)$ sẽ bằng số giao điểm của $(C_{1})$ và $(C_{2})$

2. Áp dụng vào biện luận số nghiệm phương trình

Cho phương trình $f (x) = m$ . Số nghiệm của phương trình đã cho phụ thuộc vào số giao điểm của đường thẳng $y = m$ với đồ thị hàm số $y = m$ . Trong đó đường thẳng $y = m$ tịnh tiến trên trục Oy.

3. Cách biện luận số nghiệm phương trình $f (x) = m$

a. Cách 1: Khi bài toán cho sẵn đồ thị hàm số $y = f (x)$

- Ta dựa vào sự tịnh tiến của đường thẳng $y = m$ xem nó cắt đồ thị $y = f (x)$ tại mấy điểm, từ đó biện luận phương trình có 1 nghiệm; 2 nghiệm; ... hoặc vô nghiệm khi nào tùy thuộc vào khoảng giá trị của m.

- Hình bên là đồ thị hàm số $y = x^{3} + 3 x^{2} - 2$

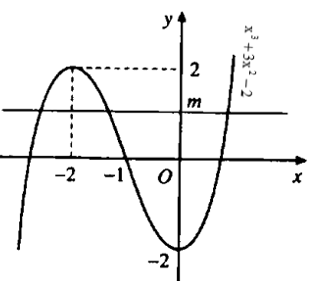
Công thức biện luận số nghiệm của phương trình dựa vào đồ thị chi tiết nhất - Toán lớp 12 (ảnh 1)