Toptailieu.vn biên soạn và giới thiệu Công thức giải phương trình mũ hay, chi tiết, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về Công thức giải phương trình mũ, từ đó học tốt môn Toán.

Công thức giải phương trình mũ chi tiết

1. Phương trình mũ cơ bản

- Phương trình mũ cơ bản có dạng:

ax=b (a>0,a≠1)

- Cách giải:                                                          

+ Cách 1: Sử dụng định nghĩa lôgarit:                  

Nếu b≤0 phương trình vô nghiệm

Nếu b >0 phương trình có nghiệm duy nhất x=logab

+ Cách 2: Sử dụng đồ thị hàm số mũ

Giao điểm của đồ thị hàm số y=ax và đường thẳng y=b là nghiệm của phương trình ax=b

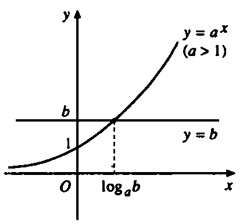
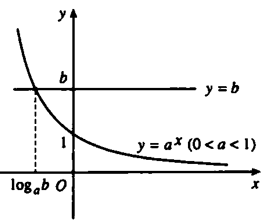
- Nhìn vào đồ thị ta thấy rõ ràng:

Khi b≤0 thì 2 đồ thị không cắt nhau tức phương trình vô nghiệm

Khi b>0 hai đồ thị chỉ cắt nhau tại 1 điểm duy nhất x=logab

2. Cách giải một số phương trình mũ đơn giản

a. Đưa về cùng cơ số

VD1. Giải các phương trình sau:

a. $2^{x^2-4x}=\frac{1}{8}$

b.$2,5^{2x-3}={\left(\frac{2}{5}\right)}^{x+1}$ 

c. $7^{x-1}=2^x$

Lời giải:

a.

$$\begin{gathered} 2^{x^2-4x}=\frac{1}{8}\iff 2^{x^2-4x}=2^{-3} \\ \iff x^2-4x=-3 \\ \iff x^2-4x+3=0\iff \left[\begin{array}{l}x=1\\ x=3\end{array}\right. \end{gathered}$$

Vậy phương trình đã cho có 2 nghiệm $x=1;x=3$

b.

$$\begin{gathered} 2,5^{2x-3}={\left(\frac{2}{5}\right)}^{x+1} \\ \iff {\left(\frac{5}{2}\right)}^{2x-3}={\left(\frac{5}{2}\right)}^{-x-1} \\ \iff 2x-3=-x-1\iff x=\frac{2}{3} \end{gathered}$$

Vậy phương trình đã cho có nghiệm $x=\frac{2}{3}$

c. 

$$\begin{gathered} 7^{x-1}=2^x\iff \frac{7^x}{7}=2^x \\ \iff {\left(\frac{7}{2}\right)}^x=7\iff x={\log }_{\frac{7}{2}}7 \end{gathered}$$

b. Đặt ẩn phụ

VD2. Giải các phương trình sau:

a. $4^x-{3.2}^x+2=0$

b. $9^{x+1}-{6.3}^{x-1}-7=0$

c. ${4.9}^x+{12}^x-{3.16}^x=0$

Lời giải:

a. 

$$\begin{gathered} 4^x-{3.2}^x+2=0 \\ \iff {\left(2^x\right)}^2-{3.2}^x+2=0 \end{gathered}$$

Đặt $t=2^x,\left(t>0\right)$. Phương trình trở thành

$t^2-3t+2=0\iff \left[\begin{array}{l}t=1\\ t=2\end{array}\right.$

Với $t=1\Rightarrow 2^x=1\iff x=0$

Với $t=2\Rightarrow 2^x=2\iff x=1$

Vậy phương trình đã cho có 2 nghiệm $x=0;x=1$

b.

$$\begin{gathered} 9^{x+1}-{6.3}^{x-1}-7=0 \\ \iff {9.9}^x-6.\frac{3^x}{3}-7=0 \\ \iff 9.{\left(3^x\right)}^2-{2.3}^x-7=0 \end{gathered}$$

Đặt $t=3^x,\left(t>0\right)$.

Phương trình trở thành:

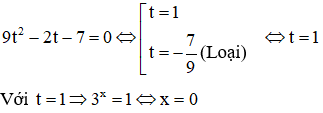
Vậy phương trình đã cho có nghiệm x = 0

c.

$$\begin{gathered} {4.9}^x+{12}^x-{3.16}^x=0 \\ \iff 4.{\left(\frac{9}{16}\right)}^x+{\left(\frac{12}{16}\right)}^x-3=0 \\ \iff 4.{\left[{\left(\frac{3}{4}\right)}^x\right]}^2+{\left(\frac{3}{4}\right)}^x-3=0 \end{gathered}$$

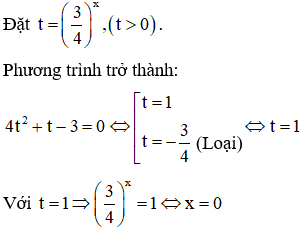
Vậy phương trình đã cho có nghiệm x = 0

c. Lôgarit hóa (lôgarit 2 vế)

VD3. Giải các phương trình sau

a. $2^x{.3}^{x^2}=1$

b. $8^{\frac{x}{x+2}}={36.3}^{2-x}$

Lời giải:

a. Lấy logarit cơ số 2 hai vế ta được:

b.

d. Đánh giá hàm số

VD4. Giải các phương trình sau

a. ${\left(\frac{1}{2}\right)}^x=x-\frac{1}{2}$

b. $9^x+2\left(x-2\right){.3}^x+2x-5=0$

Lời giải:

a. Xét hàm số: $f\left(x\right)={\left(\frac{1}{2}\right)}^x-x+\frac{1}{2}$

Ta có: $f\text{'}\left(x\right)={\left(\frac{1}{2}\right)}^x.\ln \frac{1}{2}-1<0$.

Suy ra hàm số nghịch biến

Do đó: $x<1\Rightarrow f\left(x\right)>f\left(1\right)=0$;

$x>1\Rightarrow f\left(x\right)<f\left(1\right)=0$

Vậy phương trình có nghiệm duy nhất x= 1

b.  

3. Luyện tập

Bài 1. Giải các phương trình sau:

a. $0,5^{2x-3}=1$

b. ${\left(\frac{1}{3}\right)}^{2x}=9$

c. $5^{x^2-3x+2}=25$

Bài 2. Giải các phương trình sau:

a. $3^{2x-1}+9^x=108$

b. ${25}^x-5^x-56=0$

c. $5^{2x}-7^x+7^x.17-5^{2x}.17=0$

Bài 3. Giải các phương trình sau:

a. $2^{-x}=3x+10$

b. $5^x{.2}^{\frac{2x-1}{x+1}}=50$

c. $x^{2\log x}=10x$

Bài 4. Giải các phương trình sau:

a. $2^{-x}=3x+10$

b. $3^x=11-x$

Bài 5. Giải các phương trình sau:

a. ${3.4}^x-{2.6}^x=9^x$

b. $2^x-{3.2}^{-x}=2$

c. $-8^x+{2.4}^x+2^x-2=0$

Xem thêm các dạng Toán lớp 12 hay, chi tiết khác:

Công thức logarit đầy đủ, chi tiết nhất

Công thức tính lãi suất ngân hàng chi tiết

Công thức giải bất phương trình mũ chi tiết nhất

Công thức giải phương trình lôgarit chi tiết nhất

Công thức giải bất phương trình lôgarit chi tiết nhất