Toptailieu.vn biên soạn và giới thiệu Công thứctính diện tích thiết diện của hình trụ hay, chi tiết, từ cơ bản đến nâng cao giúp học sinh nắm vững kiến thức về Công thứctính diện tích thiết diện của hình trụ, từ đó học tốt môn Toán.

Công thức tính diện tích thiết diện của hình trụ đầy đủ, chi tiết

1. Cắt hình trụ bởi mặt phẳng (P) qua trục

- Thiết diện nhận được là một hình chữ nhật.

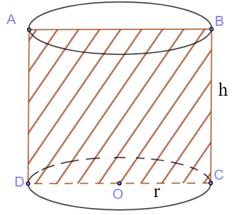
Diện tích thiết diện: $S_{ABCD}=BC.CD=2r.h$

2. Cắt hình trụ bởi mặt phẳng (P) song song và cách trục một khoảng x, $\left(x<r\right)$

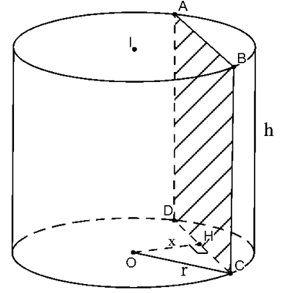
Thiết diện tạo thành là hình chữ nhật ABCD như hình trên.

Gọi H là trung điểm CD ta có $OH\perp CD\Rightarrow CD=2\sqrt{r^2-x^2}$

Do đó diện tích thiết diện $S_{ABCD}=CD.BC=2h\sqrt{r^2-x^2}$

3. Cắt hình trụ bởi mặt phẳng (P) vuông góc với trục.

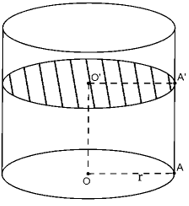
Thiết diện tạo thành là hình tròn tâm O’ bán kính $O\text{'}A\text{'}=r$

 Diện tích thiết diện: $S=\pi r^2$

4. Cắt hình trụ bởi mặt phẳng (P) không vuông góc với trục nhưng cắt tất cả các đường sinh của hình trụ.

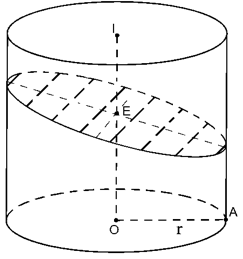
Thiết diện tạo thành là Elip (E) có trục nhỏ 2r $\Rightarrow a=r$

Trục lớn bằng $\frac{2r}{\sin \phi }\Rightarrow b=\frac{r}{\sin \phi }$ với $\phi$ là góc giữa trục OI với (P)

Do đó diện tích $S=\pi .a.b=\pi .\frac{r^2}{\sin \phi }$

5. Ví dụ áp dụng

VD1. Cho hình trụ có bán kính r, chiều cao h. Biết thiết diện qua trục là hình vuông có diện tích là 36. Tính diện tích xung quanh của hình trụ.

Lời giải:

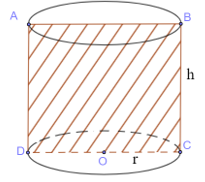
Thiết diện qua trục là hình vuông ABCD như hình.

Theo bài ta có: 

$$\begin{gathered} A{B}^2=36\Rightarrow AB=6 \\ \Rightarrow \left\{\begin{array}{l}h=6\\ r=3\end{array}\right. \end{gathered}$$

Vậy diện tích xung quanh hình trụ là $S_{xq}=2\pi r.h=36\pi$

VD2. Cho hình trụ có bán kính bằng 5cm và chiều cao bằng 12cm. Cắt hình trụ bởi mặt phẳng (P) song song với trục và cách trục một khoảng bằng 3cm. Tính diện tích thiết diện tạo bởi (P) và hình trụ.

Lời giải:

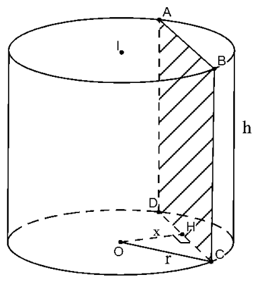
Thiết diện tạo thành là hình chữ nhật ABCD như hình

Gọi H là trung điểm CD. Khi đó khoảng cách từ (P) tới trục là $OH=3$cm

Theo Pytago ta có:

$CH=\sqrt{r^2-O{H}^2}=4\Rightarrow CD=8$cm

Do đó diện tích thiết diện là $S=8.12=96c{m}^2$

VD3. Cho hình trụ có chiều cao bằng 3 lần bán kính đáy và thể tích khối trụ là $192\pi$

Cắt hình trụ bởi một mặt phẳng (P) tạo với trục góc ${60}^{\circ }$. Khi đó (P) tạo với hình trụ thiết diện là một hình Elip. Tính diện tích thiết diện đó.

Lời giải:

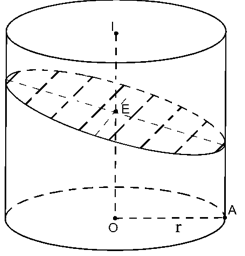
Ta có: $h=3r$

Thể tích khối trụ là :

$$\begin{gathered} V=\pi r^{2}h=3\pi r^3=192\pi \\ \Rightarrow r=4 \end{gathered}$$

Elip (E) có trục nhỏ bằng :

$2r=8\Rightarrow a=4$

Trục lớn bằng :

$\frac{2r}{\sin {60}^{\circ }}=\frac{16\sqrt{3}}{3}\Rightarrow b=\frac{8\sqrt{3}}{3}$

Do đó diện tích (E) là :

$S=\pi .a.b=\frac{32\pi \sqrt{3}}{3}$

Xem thêm các dạng Toán lớp 12 hay, chi tiết khác:

Công thức tính diện tích hình nón cụt đầy đủ nhất (diện tích xung quanh, toàn phần, đáy)

Công thức tính thể tích khối nón cụt chi tiết nhất

Công thức tính thể tích các khối tròn xoay đặc biệt chi tiết nhất

Các bài toán về tọa độ điểm, tọa độ vectơ và cách giải

Tích vô hướng và tích có hướng của hai vectơ và cách giải