Toptailieu.vn giới thiệu Giải bài tập Toán 11 Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập về phép chiếu song song. Hình biểu diễn của một hình không gian lớp 11.
Giải bài tập Toán 11 Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
Trả lời câu hỏi giữa bài:
Câu hỏi 1 trang 73 SGK Hình học 11: Hình chiếu song song của một hình vuông có thể là hình bình hành được không?
Lời giải:
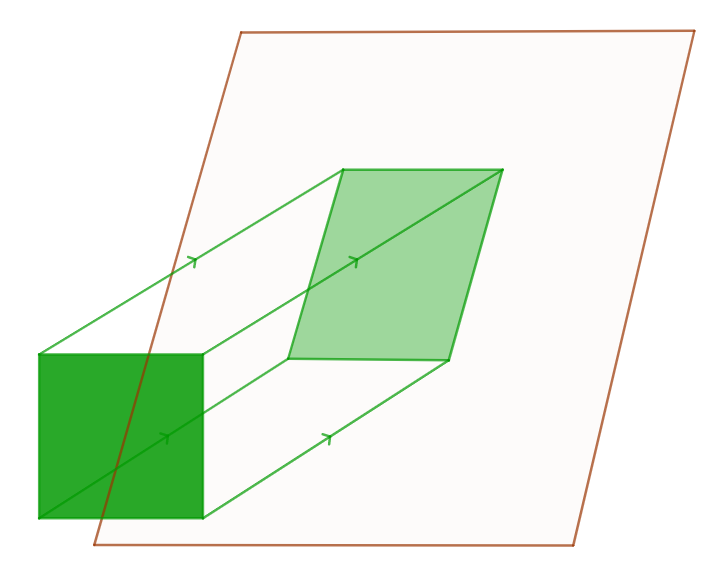
Hình chiếu song song của một hình vuông có thể là hình bình hành.
Minh họa:
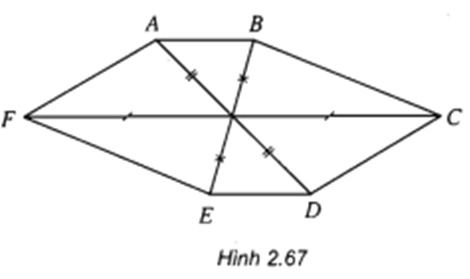
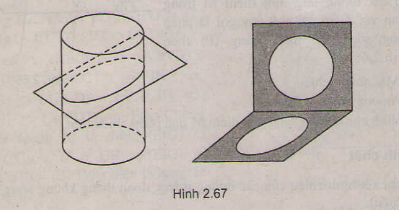
Câu hỏi 2 trang 73 SGK Hình học 11: Hình 2.67 có thế là hình chiếu song song của hình lục giác đều được không? Vì sao?
Phương pháp giải:
Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau.
Lời giải:
Hình 2.67 không thể là hình chiếu song song của hình lục giác đều vì:
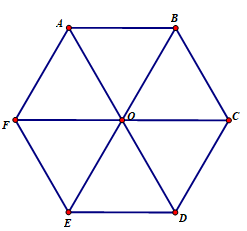
Với mọi lục giác đều ta luôn có: .
Do phép chiếu song song biến hai đường thằng song song thành hai đường thẳng song song hoặc trùng nhau.
Nên lục giác ở hình 2.67 cũng thỏa mãn:
Dễ thấy và ở hình 2.67 không song song.
Vì vậy hình 2.67 không thể là hình chiếu song song của hình lục giác đều.
Câu hỏi 3 trang 74 SGK Hình học 11: Trong các hình 2.68, hình nào biểu diễn cho hình lập phương?
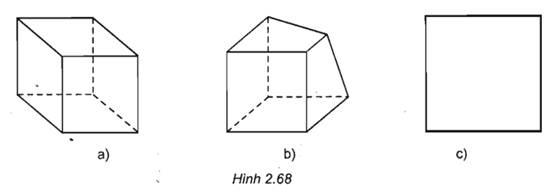
Lời giải:
Hình a biểu diễn hình lập phương.
Câu hỏi 4 trang 75 SGK Hình học 11: Các hình 2.69a, 2.69c, 2.69c là hình biểu diễn của tam giác nào?
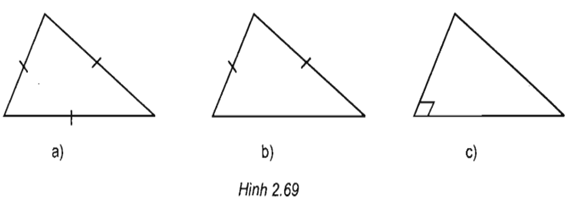
Phương pháp giải:
Dựa vào các kí hiệu về cạnh, góc.
Lời giải:
Hình 2.69a là hình biểu diễn của tam giác đều (3 cạnh bằng nhau).
Hình 2.69b là hình biểu diễn của tam giác cân (2 cạnh bằng nhau).
Hình 2.69c là hình biểu diễn của tam giác vuông (có 1 góc vuông).
Câu hỏi 5 trang 75 SGK Hình học 11: Các hình 2.70a, 2.70b, 2.70c, 2.70d là hình biểu diễn của các hình bình hành nào (hình bình hành, hình thoi, hình vuông, hình chữ nhật)?
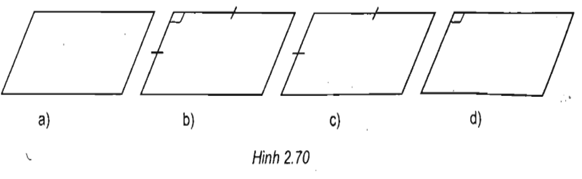
Lời giải:
Hình 2.70a biểu diễn hình bình hành
Hình 2.70b biểu diễn hình vuông
Hình 2.70c biểu diễn hình thoi
Hình 2.70d biểu diễn hình chữ nhật
Câu hỏi 6 trang 75 SGK Hình học 11: Cho hai mặt phẳng và song song với nhau. Đường thẳng cắt và lần lượt tại và . Đường thẳng song song với cắt và lần lượt tại và .
Hình 2.72 minh họa nội dung trên đúng hay sai?
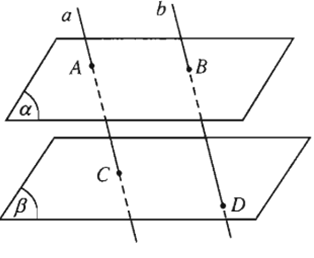
Phương pháp giải:
Sử dụng định lí 3 trang 67: Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song.
Lời giải:
Sai vì theo đề bài ta có:
nên thuộc cùng một mặt phẳng
là giao tuyến của và
là giao tuyến của và
(theo định lí 3 trang 67)
Hình 2.72 không biểu diễn được
Lý thuyết Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
1. Lý thuyết Hình biểu diễn của hình không gian trên mặt phẳng
Hình biểu diễn của một hình H trong không gian là hình chiếu song song của
hình H lên một mặt phẳng nào đó theo một phương chiếu nào đó hoặc hình
đồng dạng với hình chiếu đó.
Chú ý:
a) Hình biểu dễn của hình bình hành nói chung là hình bình hành ( trường hợp đặc biệt thì là một đoạn thẳng)
b) Hình biểu diễn của hình thang là một hình thang ( trường hợp đặc biệt thì là một đoạn thẳng)
c) Hình biểu diễn của hình thoi, hình chữ nhật, hình vuông đều là hình bình hành (đặc biệt là một đoạn thẳng)
d) Một tam giác bất kì đều có thể xem là hình biểu diễn của tam giác cân, tam giác vuông, tam giác đều
e) Hình biểu diễn của một đường tròn là một đường elip hoặc một đường tròn, hoặc đặc biệt có thể là một đoạn thẳng (h.2.67)
2. Lý thuyết Tính chất phép chiếu song song
Ta chỉ xét hình chiếu của đường thẳng, đoạn thẳng không song song với phương chiếu
a) Phép chiếu song song biến ba điểm thẳng hàng thành ba điểm thẳng hàng và không làm thay đổi thứ tự ba điểm đó
b) Phép chiếu song song biến đường thẳng thành đường thẳng, tia thành tia, đoạn thẳng thành đoạn thẳng
c) Phép chiếu song song biến hai đường thẳng song song thành hai đường thẳng song song hoặc trùng nhau
d) Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng nằm trên hai đường thẳng song song hoặc cùng nằm trên một đường thẳng.
3. Lý thuyết Định nghĩa phép chiếu song song
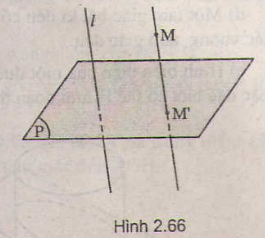
Cho và đường thẳng cắt . Với mỗi điểm trong không gian vẽ đường thẳng qua và song song ( hoặc trùng ) với , cắt tại
Phép đặt tương ứng mỗi điểm trong không gian với điểm như vậy gọi là phép chiếu song song lên mặt phẳng theo phương (h.2.66)
: Mặt phẳng chiếu
: phương chiếu
: Hình chiếu song song của điểm qua phép chiếu trên