Toptailieu.vn giới thiệu Giải bài tập Toán 11 Bài 3: Đường thẳng vuông góc với mặt phẳng chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập về đường thẳng vuông góc với mặt phẳng lớp 11.
Giải bài tập Toán 11 Bài 3: Đường thẳng vuông góc với mặt phẳng
Trả lời câu hỏi giữa bài:
Lời giải:
Muốn chứng minh đường thẳng vuông góc với một mặt phẳng , người ta phải chứng minh vuông góc với hai đường thẳng cắt nhau thuộc mặt phẳng .
Lời giải:
Không vì nội dung định lí yêu cầu và cắt nhau.
Ví dụ: trường hợp cùng thuộc một mặt phẳng mà nhưng chứ không vuông góc .
Bài tập trang 104, 105 SGK Toán 11
a) Nếu và thì
b) Nếu và thì
c) Nếu và thì
d) Nếu và thì
Phương pháp giải:
Liên hệ giữa quan hệ song song và quan hệ vuông góc giữa đường thẳng và mặt phẳng.
Lời giải:
a) Đúng
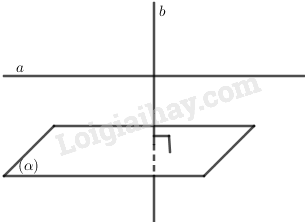
b) Sai vì có thể song song hoặc cắt
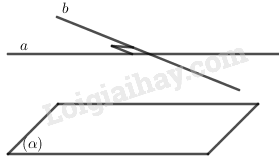
c) Sai vì vẫn có thể xảy ra trường hợp cắt hoặc chéo
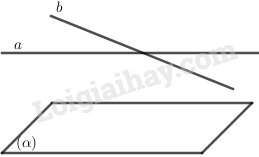
d) Sai vì vẫn có thể xảy ra trường hợp
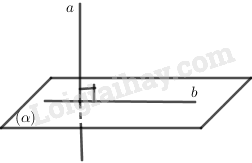
a) Chứng minh rằng vuông góc với mặt phẳng .
b) Gọi là đường cao của tam giác , chứng minh rằng vuông góc với mặt phẳng .
Phương pháp giải:
Sử dụng kết quả của định lí:
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Lời giải:
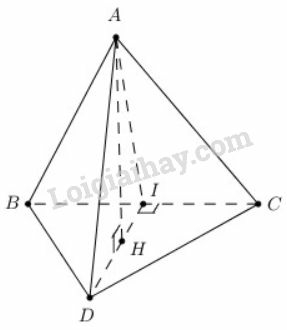
a) Tam giác cân tại nên ta có đường trung tuyến ứng với cạnh đáy đồng thời là đường cao do đó:
Tương tự ta có:
Ta có:
b) Ta có là đường cao của tam giác nên
Mặt khác: mà nên
Ta có
a) Đường thẳng vuông góc với mặt phẳng ;
b) Đường thẳng vuông góc với mặt phẳng và đường thẳng vuông góc với mặt phẳng .
Phương pháp giải:
Sử dụng kết quả của định lí:
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Lời giải:

a) nên tam giác cân tại .
là giao của hai đường chéo hình bình hành nên là trung điểm của và .
Do đó vừa là trung tuyến đồng thời là đường cao trong tam giác hay
Chứng minh tương tự ta được:
Ta có:
b) là hình thoi nên
a) H là trực tâm của tam giác ;
b)
Phương pháp giải:
a) Chứng minh .
b) Sử dụng hệ thức lượng trong tam giác vuông.
Lời giải:
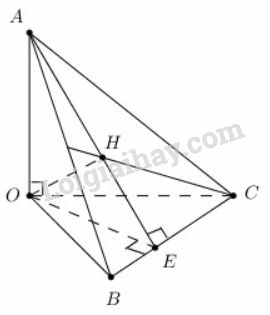
a) là hình chiếu của trên mp nên .
Mặt khác: ,
Mà (1)
Ta có:
Mà
Do đó (2)
Từ (1) và (2) ta có tam giác có
là trực tâm của tam giác .
b) Trong mặt phẳng gọi
Ta có: vuông tại có đường cao
(hệ thức giữa cạnh và đường cao trong tam giác vuông )
Lại có:
Mà nên vuông tại có là đường cao.
Vậy (đpcm).
Nhận xét: Biểu thức này là mở rộng của công thức tính đường cao thuộc cạnh huyền của tam giác vuông:
a) ;
b) Nếu trong mặt phẳng kẻ vuông góc với tại thì vuông góc mặt phẳng .
Phương pháp giải:
Sử dụng kết quả của định lí:
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
Lời giải:
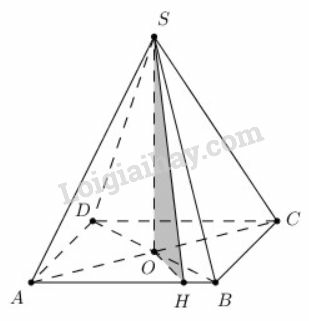
a) cân tại .
là trung điểm của là đường trung tuyến đồng thời là đường cao của tam giác cân nên
Chứng minh tương tự ta có:
Ta có:
hay .
b)
a) vuông góc với ;
b) vuông góc với mặt phẳng .
Phương pháp giải:
a) Chứng minh .
b) Chứng minh .
Lời giải:
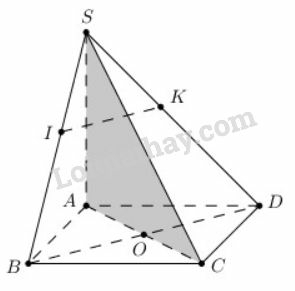
a) là hình thoi nên (1)
Theo giả thiết: (2)
Từ (1) và (2) suy ra (Tính chất một đường vuông góc với 2 cạnh của một tam giác thì vuông góc với cả cạnh còn lại của tam giác ấy)
Cách khác:
Sử dụng định lí ba đường vuông góc:
Ta có: là hình chiếu của lên .
Mà
b) Ta có: theo định lí Ta-lét ta có
Theo a) ta có: .
a) và ;
b) .
Phương pháp giải:
a) Sử dụng kết quả của định lí:
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.
b) Chứng minh .
Lời giải:
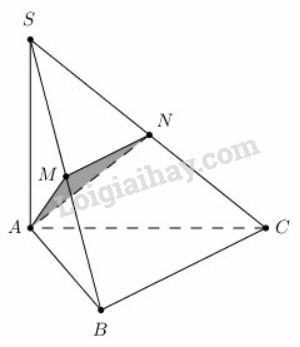
a) (1),
Tam giác vuông tại nên (2)
Từ (1) và (2) suy ra .
nên (3)
(giả thiết) (4)
Từ (3) và (4) suy ra .
b) nên (5)
nên theo định lí ta lét ta có:
Ta có:
(6)
Từ (5) và (6) suy ra suy ra
Nhận xét: Hình chóp trong các bài 4; 6; 7 thuộc loại hình chóp có một cạnh bên vuông góc với đáy (do đó nó có hai mặt bên vuông góc với đáy).
a) Hai đường thẳng xiên bằng nhau khi và chỉ khi hai hình chiếu của chúng bằng nhau;
b) Với hai đường xiên cho trước, đường xiên nào lớn hơn thì có hình chiếu lớn hơn và ngược lại đường xiên nào có hình chiếu lớn hơn thì lớn hơn.
Phương pháp giải:
a) Chứng minh các tam giác vuông bằng nhau.
b) Sử dụng định lí Pytago.
Lời giải:
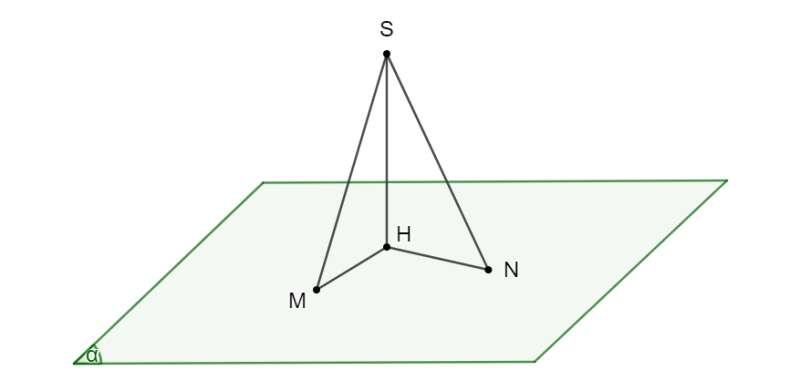
a) Gọi là một đường xiên khác.
vuông tại .
Xét hai tam giác vuông và có cạnh chung.
Nếu (cạnh huyền - cạnh góc vuông)
.
Ngược lại nếu thì (hai cạnh góc vuông)
.
b) Xét tam giác vuông và có cạnh chung.
Giả sử
Áp dụng định lí Pytago vào hai tam giác vuông và ta được:
Phần đảo chứng minh tương tự
Lý thuyết Bài 3. Đường thẳng vuông góc với mặt phẳng
1. Định nghĩa
Một đường thẳng gọi là vuông góc với mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng ấy.
Định lí 1:
Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì đường thẳng d vuông góc với mặt phẳng (P).
Hệ quả: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó cũng vuông góc với cạnh thứ ba.
2. Tính chất
Tính chất 1.
Có duy nhất một mặt phẳng (P) đi qua một điểm O cho trước và vuông góc với một đường thẳng a cho trước.
Mặt phẳng vuông góc với AB tại trung điểm O của đoạn AB, gọi là mặt phẳng trung trực của đoạn thẳng AB (h.3.26).
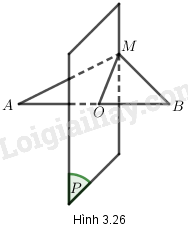
3. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng
Tính chất 3.
a) Mặt phẳng nào vuông góc với một trong hai đường thẳng song song thì cũng vuông góc với đường thẳng còn lại.
b) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng song song với nhau.
Tính chất 5.
a) Cho đường thẳng a và mặt phẳng (P) song song với nhau. Đường thẳng nào vuông góc với (P) thì cũng vuông góc với a.
b) Nếu một đường thẳng và một mặt phẳng (không chứa đường thẳng đó) cùng vuông góc với một đường thẳng khác thì chúng song song với nhau.
4. Phép chiếu vuông góc
Định nghĩa:
Phép chiếu song song lên mặt phẳng (P) theo phương l vuông góc với mặt phẳng (P) gọi là phép chiếu vuông góc lên mặt phẳng (P).
Định lí ba đường vuông góc:
Cho đường thẳng a không vuông góc với mặt phẳng (P) và đường thẳng b nằm trong (P). khi đó điều kiện cần và đủ để b vuông góc với a là b vuông góc với hình chiếu a' của a trên (P) (h.3.27).

5. Góc giữa đường thẳng và mặt phẳng
Định nghĩa:
Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói rằng góc giữa a và (P) bằng
Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa a và hình chiếu a' của nó trên (P), gọi là góc giữa đường thẳng a và mặt phẳng (P) (h.3.28).
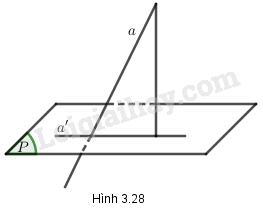
Chú ý: góc giữa đường thẳng và mặt phẳng không vượt quá
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.