A. Lý thuyết

Cho tam giác ABC vuông tại A. Có AB = c, AC = b, BC = a.

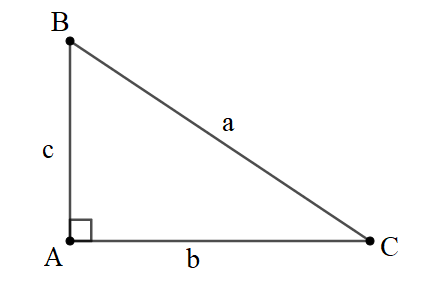
Ta có các hệ thức giữa góc và cạnh trong tam giác vuông:

Cạnh góc vuông = (cạnh huyền) x (sin góc đối) = (cạnh huyền) x (cos góc kề)

$\begin{array}{l}c=a.\sin \widehat{C}=a.\cos \widehat{B}\\ b=a.\sin \widehat{B}=a.\cos \widehat{C}\end{array}$

Cạnh góc vuông = (cạnh góc vuông còn lại) x (tan góc đối) = (cạnh góc vuông còn lại) x (cot góc kề)

$\begin{array}{l}c=b.\tan \widehat{C}=b.\cot \widehat{B}\\ b=c.\tan \widehat{B}=c.\cot \widehat{C}\end{array}$

B. Các dạng bài

Dạng 1: Giải tam giác vuông

Phương pháp giải:

Tính độ dài các cạnh và số đo các góc dựa vào dữ kiện cho trước của bài toán. Áp dụng hệ thức giữa cạnh và các góc của một tam giác vuông để tính toán.

Ví dụ minh họa:

Bài 1: Cho tam giác ABC vuông tại A. Biết BC = 10cm, $\widehat{C}={30}^o$. Tính AB, AC.

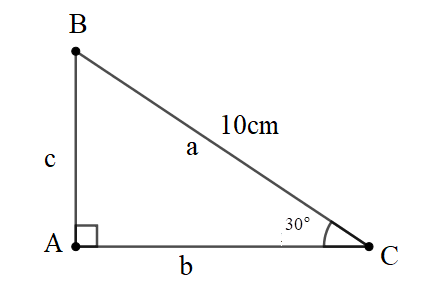
Giải:

+) Áp dụng hệ thức giữa góc và cạnh trong tam giác vuông ta có:

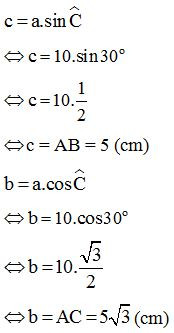
Bài 2: Cho tam giác ABC vuông tại A. Có BC = 16cm, $\widehat{C}={30}^o$. Tính số đo $\hat{B}$ và AC.

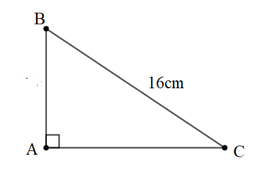
Giải:

+) Áp dụng hệ thức giữa góc và cạnh trong tam giác vuông ta có:

Dạng 2: Tính số đo góc, cạnh, đoạn thẳng trong tam giác thường

Phương pháp giải:

Bằng cách kẻ thêm đường cao ta làm xuất hiện tam giác vuông để áp dụng các hệ thức giữa cạnh và góc thích hợp.

Ví dụ minh họa:

Bài 1: Cho tam giác ABC có AH là đường cao ứng với cạnh BC. Biết $\widehat{B}={30}^o$, AB = 10cm. Tính BH.

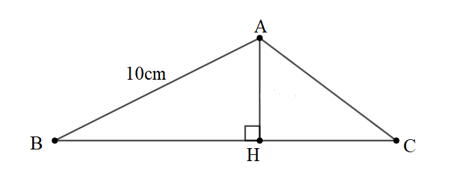
Giải:

Xét tam giác ABH vuông tại H (do AH là đường cao)

+) Áp dụng hệ thức giữa góc và cạnh trong tam giác vuông ta có:

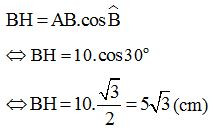
Bài 2: Cho tam giác ABC có $\widehat{B}={60}^o$, hình chiếu của cạnh AB trên BC có độ dài là 4cm, AB : AC = 1 : 2. Tính độ dài AB, AC và số đo $\hat{C}$.

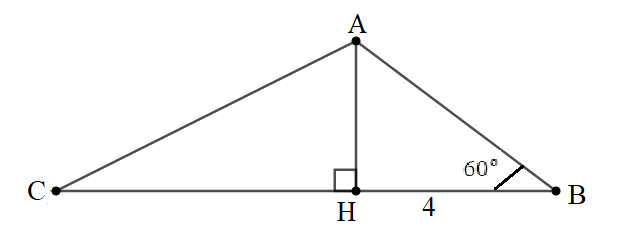
Giải:

+) Kẻ đường cao AH, HB chính là hình chiếu của AB trên BC.

+)  Xét tam giác AHB vuông tại H:

Áp dụng hệ thức giữa góc và cạnh trong tam giác vuông ta có:

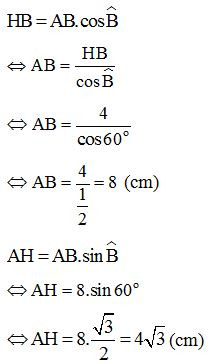
+) Ta lại có AB : AC = 1 : 2$\Rightarrow$AC = 2AB$\Rightarrow$AC = 2.8 = 16 (cm)

+) Xét tam giác AHC vuông tại H ta có:

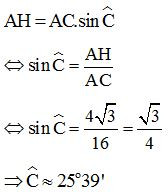
Dạng 3: Bài toán thực tế

Phương pháp giải:

Vẽ hình minh họa đề bài (thường là tam giác vuông, tam giác thường có đường cao). Áp dụng hệ thức về góc và cạnh trong tam giác vuông để tính toán giá trị bài toán yêu cầu.

Ví dụ minh họa:

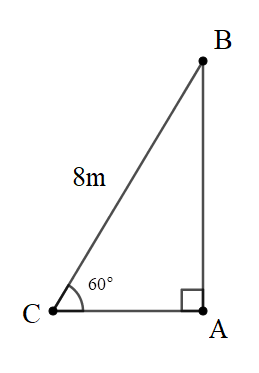
Bài 1: Để hái một buồng cau xuống, người nông dân phải đặt thang tre sao cho đầu thang tre đạt độ cao đến buồng cau đó, khi đó góc của thang tre với mặt đất là $60°$, biết chiếc thang dài 8m. Tính độ cao cây cau. (coi cây cau thẳng đứng)

Giải:

+) Ta có hình vẽ: AB là cây cau, AC là mặt đất, BC là cái thang.

+) Xét tam giác ABC vuông tại A.

Áp dụng hệ thức về góc và cạnh trong tam giác vuông:

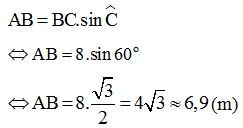
Vậy cây cau cao khoảng 6,9m.

Bài 2: Một máy bay đang bay. Khi bay hạ cánh xuống mặt đất, đường đi của máy bay tạo một góc $5°$ với mặt đất. Biết từ khi hạ cánh đến khi tiếp đất, máy bay bay được quãng đường 20km. Vậy từ độ cao bao nhiêu kilômét so với mặt đất phải bắt đầu cho máy bay hạ cánh ?

Giải:

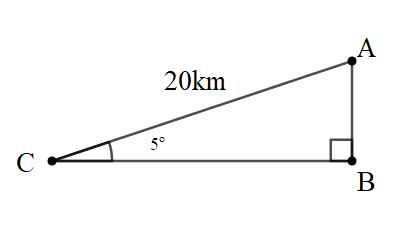
+) Ta có hình vẽ: A là điểm máy bay bắt đầu hạ cánh. C là điểm máy bay tiếp đất. AC là quãng đường bay.

+) Xét tam giác ABC vuông tại B. 

Áp dụng hệ thức về góc và cạnh trong tam giác vuông:

$\begin{array}{l}AB=AC.\sin \widehat{C}\end{array}$

$\iff AB=20.\sin 5^o$

$\iff AB\approx 1,74$ (km)

Vậy độ cao 1,74 kilômét so với mặt đất phải bắt đầu cho máy bay hạ cánh.

C. Bài tập tự luyện

Bài 1: Cho tam giác ABC vuông tại A. Biết $\widehat{B}={50}^o$, AB = 8cm. Tính BC, AC.

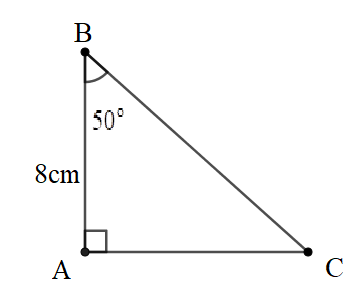
Đáp án: AC = 9,53cm; BC = 12,45cm

Bài 2: Cho tam giác ABC vuông tại A. Biết BC = 10cm, AC = 6cm. Tính AB và số đo $\hat{B}, \hat{C}$.

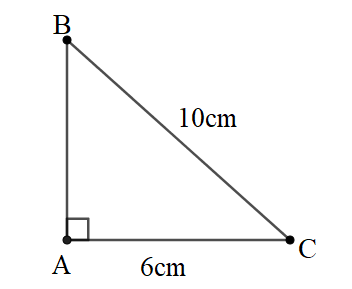
Đáp án: AB = 8cm; $\widehat{C}\approx {53}^{o}8\text{'};\widehat{B}\approx {36}^{o}52\text{'}$

Bài 3: Cho tam giác MPN vuông tại P. Có đường cao PK, biết PN = 6cm, $\widehat{N}={45}^o$. Tính độ dài PK.

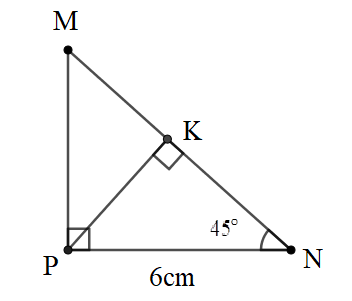
Đáp án: $PK=3\sqrt{2}$ (cm)

Bài 4: Cho hình chữ nhật ABCD. Có đường chéo AC = 10cm, $\widehat{BAC}={30}^o$. Tính độ dài cạnh AB.

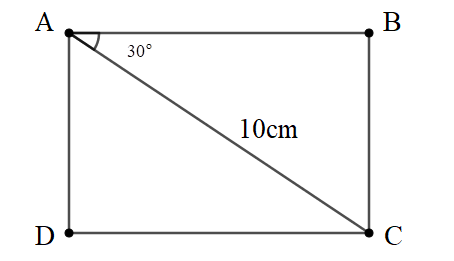
Đáp án: $AB=5\sqrt{3}$ (cm)

Bài 5: Cho tam giác ABC có đường cao AH. Biết AH = 4cm, $\widehat{C}={34}^o$. Tính AC.

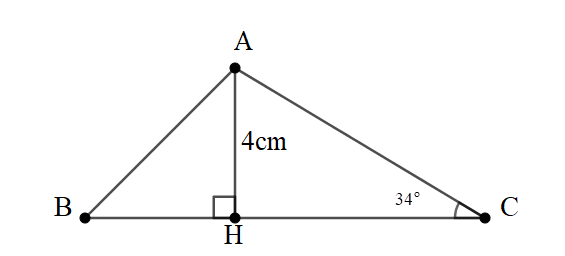
Đáp án: AC = 7,15cm

Bài 6: Cho tam giác ABC có đường cao AH. Biết AH = 7cm, $\widehat{ABC}={45}^o$, $\widehat{BAC}={104}^o$. Tính AC.

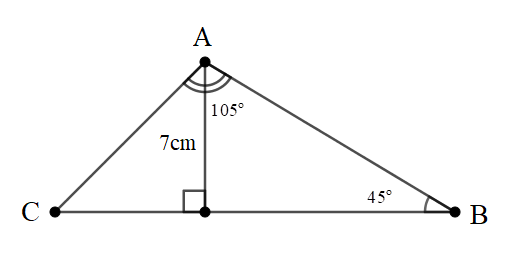
Đáp án: AC = 14cm

Bài 7: Cho tam giác ABC có AH là đường cao. Biết AB = 7cm, $\widehat{ABC}={56}^o,$$\widehat{BAC}={80}^o$. Tính BH,CH.

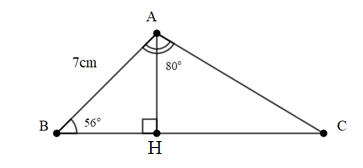
Đáp án: BH = 3,91cm ; CH = 6cm.

Bài 8: Cho hình thoi ABCD. Biết độ dài đường chéo AC = 10cm, $\widehat{BAC}={30}^o$. Tính độ dài đường chéo BD.

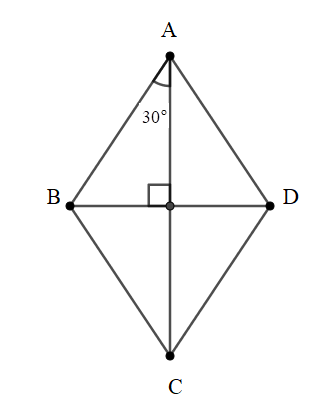
Đáp án: $BD=\frac{10}{\sqrt{3}}$ (cm)

Bài 9: Tháp đèn có hình bát giác, cao 66 m so với mực nước biển. Ngọn đèn đặt trong tháp có thể phát sáng xa 40 km. Môt người trên biển muốn quan sát ngọn hải đăng có độ cao 66 m, người đó đứng trên mũi thuyên và dùng giác kế đo được góc giữa thuyền và tia nắng chiều từ đỉnh ngọn hải đăng đến thuyền là $25°$. Tính khoảng cách của thuyền đến ngọn hải đăng.

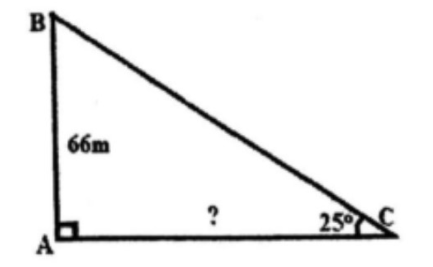
Đáp án: 142m

Bài 10: Trường bạn An có một chiếc thang dài 6 mét. Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo được với mặt đất một góc “an toàn” là $65°$.

Đáp án: 2,5m

Bài 11: Từ một đài quan 350 m so với mực nước biển, người ta nhìn thấy một chiếc thuyền bị nạn dưới góc $20°$ so với phương ngang của mực nước biển. Muốn đến cứu con thuyền thì phải đi quãng đường dài bao nhiêu mét?

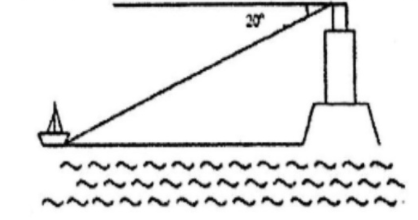
Đáp án: 961,6m

Bài 12: Thang xếp chữ A gồm 2 thang đơn tựa vào nhau. Để an toàn, mỗi thang đon tạo với mặt đất một góc khoảng $75°$. Nếu muốn tạo một thang xếp chữ A cao 2m tính từ mặt đất thì mỗi thang đơn phải dài bao nhiêu ?

Đáp án: 2,07m