Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông trang 84,85,86,87,88 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:
Nội dung bài viết
VBT Toán lớp 9 Bài 1:Một số hệ thức về cạnh và đường cao trong tam giác vuông
Phần câu hỏi bài 1 trang 84, 85 Vở bài tập toán 9 tập 1
Câu 1.
Hãy khoanh tròn vào chữ cái đứng trước kết quả đúng. Xem hình 18.
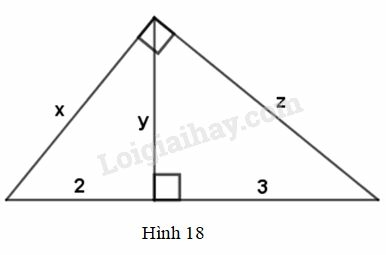
Giá trị của x là:
(A) √6 (B) √10
(C) √12 (D) √15
Phương pháp giải:
Áp dụng hệ thức a2=c.a′ để tính giá trị của cạnh góc vuông khi biết độ dài cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Trả lời:
Áp dụng hệ thức a2=c.a′ ta có : x2=(2+3).2 ⇔x2=10⇔x=√10
Đáp án cần chọn là B.
Câu 2.
Giá trị của y là:
(A) √6 (B) √10
(C) √12 (D) √15
Phương pháp giải:
Áp dụng kiến thức : Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
Trả lời:
Tam giác vuông có h2=a′.b′
Nên y2=2.3=6⇔y=√6
Đáp án cần chọn là A.
Câu 3.
Giá trị của z là:
(A) √6 (B) √10
(C) √12 (D) √15
Phương pháp giải:
Cách 1: Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Cách 2: Áp dụng định lí Pi-ta-go.
Trả lời:
Áp dụng hệ thức b2=c.b′ trong tam giác vuông đã cho, ta có:z2=(2+3).3=15⇔z=√15
Đáp án cần chọn là D.
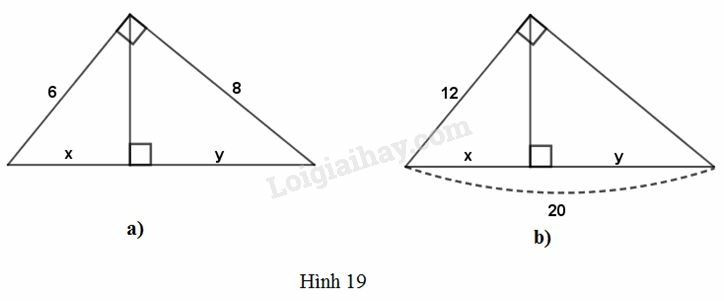
Phương pháp giải:
- Áp dụng định lí Pi-ta-go để tìm độ dài cạnh huyền.
- Áp dụng kiến thức : Trong tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Trả lời:
a) x+y=√62+82=10
62=10x⇒x=36:10=3,6
82=10.y⇒y=64:10=6,4
b) 122=20x⇒x=14420=7,2.
y=20−7,2=12,8
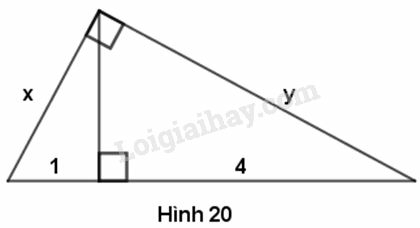 Phương pháp giải:
Phương pháp giải:Áp dụng hệ thức liên quan đến cạnh góc vuông, cạnh huyền và hình chiếu của góc vuông lên cạnh huyền để tìm giá trị của x, y.
Trả lời:
x2=(1+4).1=5
⇒x=√5
y2=(1+4).4=20⇒y=√20
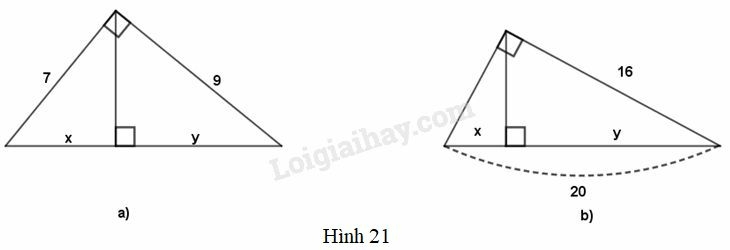 Phương pháp giải:
Phương pháp giải:- Dùng định lí Pi-ta-go tính giá trị của cạnh huyền.
- Dùng hệ thức về cạnh góc vuông, cạnh huyền và hình chiếu trên cạnh huyền để tìm độ dài các cạnh còn thiếu.
Trả lời:
a) x+y=√72+92=√130
72=√130⇒x=49:√130=49√130
92=√130y⇒y=81:√130=81√130
b) 162=20.y⇒y=256:20=12,8
x=20−12,8=7,2
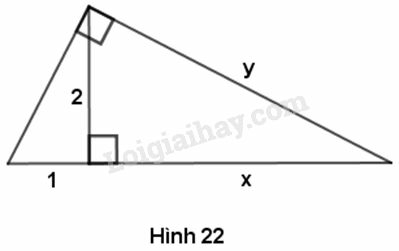 Phương pháp giải:
Phương pháp giải:- Vận dụng kiến thức : Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền để tìm cạnh x.
- Tìm y bằng cách dùng hệ thức liên quan đến cạnh góc vuông, cạnh huyền và hình chiếu của cạnh góc vuông.
Trả lời:
22=1.x⇒x=4
y2=22+42=4+16=20
⇒y=√20
Cách khác : y2=5x=5.4=20⇒y=√20
Bài 5 trang 86 Vở bài tập toán 9 tập 1:Hãy tính x và y trong hình sau: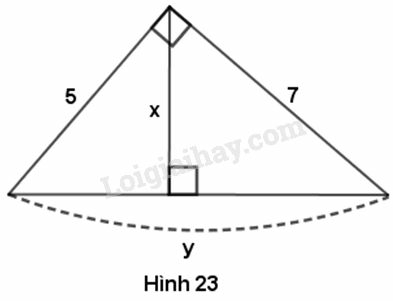 Phương pháp giải:
Phương pháp giải:
Vận dụng kiến thức : Trong tam giác vuông, tích hai cạnh góc vuông bằng tích của đường cao và cạnh đáy tương ứng.
Trả lời:
y=√52+72=√74
xy=5.7=35
⇒x=35y=35√74
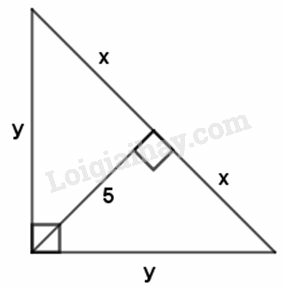
Phương pháp giải:
Dùng tính chất của tam giác vuông cân hoặc hệ thức lượng về chiều cao và hình chiếu để tìm giá trị của x và y.
Trả lời:
Do các tam giác tạo thành là những tam giác vuông cân nên x=5 và y=√52+52=5√2
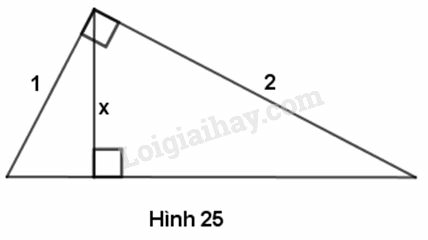
Phương pháp giải:
Vận dụng kiến thức : Trong tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.
Trả lời:
1x2=112+122=1+14=54 ⇒x2=45⇒x=√45 =4√55
Phương pháp giải:
- Dùng định lí Pi-ta-go tính độ dài cạnh huyền.
- Dùng các hệ thức về cạnh và đường cao của tam giác vuông để tìm độ dài các cạnh.
Trả lời:
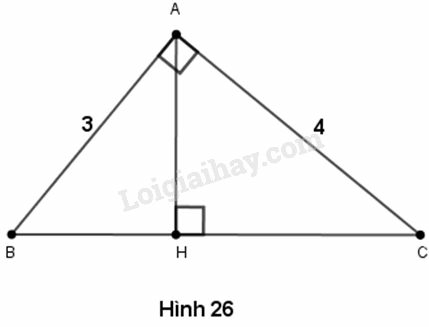
Xét tam giác vuông ABC. Theo định lí Pytago, ta có:
BC=√32+42=√25=5
Theo các hệ thức về cạnh và đường cao của tam giác vuông, ta có:
AB2=BC.BH⇒32=5.BH⇒BH=95=1,8;CH=BC−BH=5−95=165;AH.BC=AC.AB⇒AH.5=3.4⇒AH=12:5=2,4
Phương pháp giải
- Tìm x : Vận dụng kiến thức “Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền”.
- Tìm y : Dùng định lí Pi-ta-go hoặc hệ thức lượng về các cạnh và đường cao trong tam giác vuông.
Trả lời:
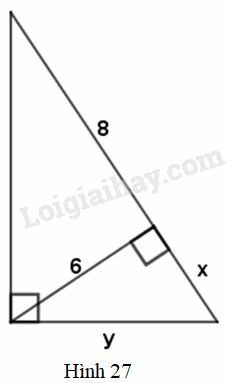
62=8.x⇒x=36:8=4,5
y=√62+4,52=√36+20,25=7,5
a) Tam giác DIL là một tam giác cân
b) Tổng IDI2+IDK2 không dổi khi I thay đổi trên cạnh AB.
Phương pháp giải:
- Vẽ hình theo các giả thiết đã cho.
- Áp dụng hệ thức : 1h2=1b2+1c2
Trả lời:
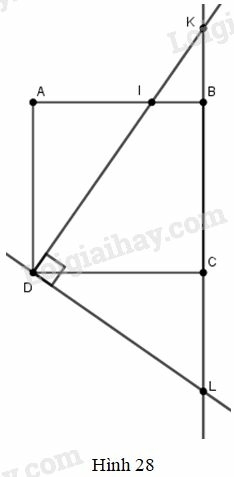
a) Hai tam giác vuông DAI và DCL có DA=DC (là hai cạnh của hình vuông ABCD);^ADI=^CDL (cùng phụ với góc ^CDI) nên chúng bằng nhau.
Suy ra DI=DL
Tam giác DIL có hai cạnh bên bằng nhau nên nó là một tam giác cân.
b) Theo câu a) ta có :
1DI2+1DK2=1DL2+1DK2 (1)
Mặt khác, tam giác vuông DKL có DC là đường cao ứng với cạnh huyền nên
1DL2+1DK2=1DC2 (2)
Từ (1) và (2) suy ra
1DI2+1DK2=1DC2
Vì DC là cạnh của hình vuông ABCD đã cho nên độ dài của DC không đổi, tức là 1DI2+1DK2=1DC2 không đổi khi I thay đổi trên cạnh AB.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.