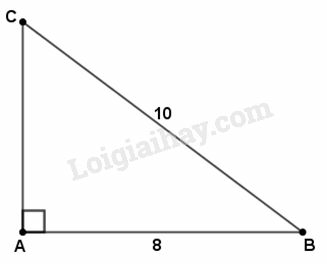
Trong tam giác vuông , theo định lí Pi-ta-go, ta có :
Do đó:
Vì và là hai góc phụ nhau nên :
.
Bài 12 trang 91 Vở bài tập toán 9 tập 1
Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn 45o
sin60o; cos75o; sin52o30’; cot82o; tan80o
Phương pháp giải:
- Vận dụng kiến thức : Cho hai góc và phụ nhau .
Ta có: .
Trả lời:
Bài 13 trang 91 Vở bài tập toán 9 tập 1
Cho tam giác ABC vuông tại A, . Hãy tính cạnh AB (làm tròn đến chữ số thập phân thứ ba), biết rằng
Phương pháp giải:
Sử dụng định nghĩa các tỉ số lượng giác , thay giá trị của và độ dài cạnh huyền BC đã biết để tìm độ dài cạnh kề AB.
Trả lời:
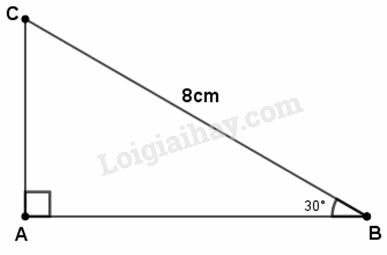
Trong tam giác vuông theo định nghĩa các tỉ số lượng giác, ta có :
Suy ra
Bài 14 trang 91 Vở bài tập toán 9 tập 1
Dựng góc nhọn , biết
Phương pháp giải:
Dựng tam giác vuông với góc nhọn có cạnh đối bằng đơn vị độ dài; cạnh kề bằng đơn vị độ dài.
Trả lời:
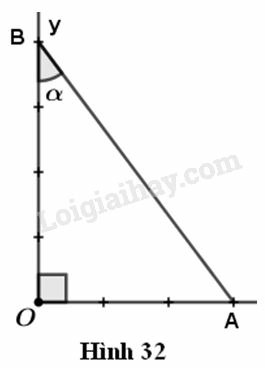
Dựng góc vuông . Lấy một đoạn thẳng làm đơn vị. Trên tia , lấy điểm sao cho Trên tia lấy điểm B sao cho Góc là góc cần dựng.
Thật vậy, trong tam giác vuông ta có :
Bài 15 trang 92 Vở bài tập toán 9 tập 1
Cho tam giác ABC vuông tại A, , AB= 6 cm. Biết
Hãy tính :
a) Cạnh AC ; b) Cạnh BC.
Phương pháp giải:
- Dựa vào tỉ số lượng giác : và giá trị ; độ dài cạnh đã biết để tìm giá trị của cạnh
- Dùng định lí Pi-ta-go để tìm độ dài cạnh BC khi biết độ dài hai cạnh còn lại của tam giác vuông.
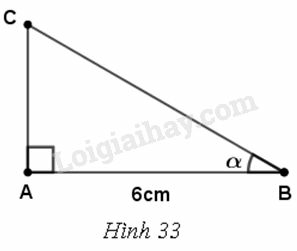
Trả lời:
a) Theo định nghĩa các tỉ số lượng giác, ta có :
Suy ra
b) Trong tam giác vuông theo định lí Pi-ta-go ta có :
Bài 16 trang 92 Vở bài tập toán 9 tập 1
Cho tam giác ABC vuông tại A. Biết hãy tính các tỉ số lượng giác của góc C.
Phương pháp giải:
Vận dụng kiến thức :
- Cho góc nhọn . Ta có
- Cho hai góc và phụ nhau . Ta có:
Trả lời:
Ta có , suy ra :
Mặt khác, ta có :
.
Vì trong tam giác vuông có và là hai góc phụ nhau nên :
Bài 17 trang 92 Vở bài tập toán 9 tập 1
Tìm x trong hình 34
Phương pháp giải:
- Dựa vào tỉ số lượng giác, tìm độ dài cạnh a.
- Dựa vào định lí Pi-ta-go, tính độ dài cạnh x.
Trả lời:
Chú ý:
Cách giải chi tiết hơn:
Vẽ lại hình và đặt tên các góc như hình sau:
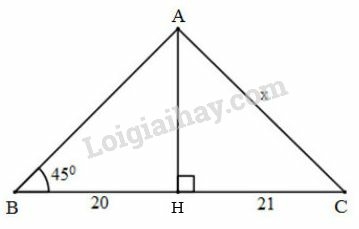
Xét tam giác vuông tại có , nên:
Áp dụng định lí Pytago vào tam giác vuông tại , ta có:
Vậy
Bài 18 trang 93 Vở bài tập toán 9 tập 1
Tìm x trong mỗi hình sau (làm tròn đến chữ thập phân thứ ba), biết rằng
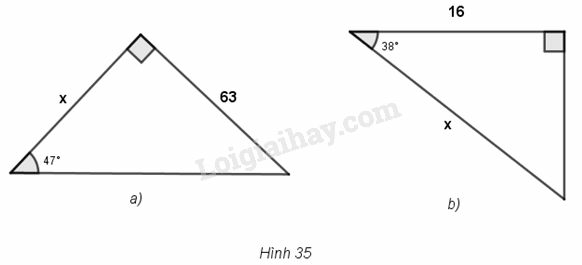
Phương pháp giải:
a) Dựa vào tỉ số lượng giác để tìm độ dài cạnh chưa biết.
b) Dựa vào tỉ số lượng giác để tìm độ dài cạnh chưa biết.
Trả lời:
a) Ta có :
Suy ra
b) Ta có
Suy ra
Bài 19 trang 93 Vở bài tập toán 9 tập 1
Xét quan hệ giữa hai góc trong mỗi biểu thức rồi tính:
a)
b)
Phương pháp giải:
Vận dụng kiến thức : Cho hai góc và phụ nhau . Ta có:
Trả lời:
a) Ta có : do đó hai góc và là hai góc phụ nhau nên
Vậy
b) Ta có : do đó hai góc và là hai góc phụ nhau nên
Vậy