Câu 8

Hãy điền vào chỗ trống dấu $>,<,=$ để được khẳng định đúng :

$\sin {27}^o.......\sin {30}^o$

Phương pháp giải:

Vận dụng kiến thức : Khi góc $\alpha$ tăng từ $0^o$ đến ${90}^o\left(0^o<\alpha <{90}^o\right)$ thì $\sin \alpha$ và $\tan \alpha$ tăng còn $\cos \alpha$ và $\cot \alpha$ giảm.

Trả lời:

$\sin {27}^o<\sin {30}^o$

Dấu cần điền vào chỗ trống là dấu $<$.

Câu 9

$\cos {50}^o.......\cos {38}^o$

Phương pháp giải:

Vận dụng kiến thức : Khi góc $\alpha$ tăng từ $0^o$ đến ${90}^o\left(0^o<\alpha <{90}^o\right)$ thì $\sin \alpha$ và $\tan \alpha$ tăng còn $\cos \alpha$ và $\cot \alpha$ giảm.

Trả lời:

$\cos {50}^o<\cos {38}^o$

Dấu cần điền vào chỗ trống là dấu $<$

Câu 10

$\tan {40}^o.........1$

Phương pháp giải:

Vận dụng kiến thức : Khi góc $\alpha$ tăng từ $0^o$ đến ${90}^o\left(0^o<\alpha <{90}^o\right)$ thì $\sin \alpha$ và $\tan \alpha$ tăng còn $\cos \alpha$ và $\cot \alpha$ giảm.

Trả lời:

$\tan {40}^o<\tan {45}^o$ hay $\tan {40}^o<1$

Dấu cần điền vào chỗ trống là dấu $<.$

Câu 11

$\tan {40}^o.......\cot {50}^o$

Phương pháp giải:

Vận dụng kiến thức : Hai góc $\alpha$ và $\beta$ phụ nhau $\left(\alpha +\beta ={90}^o\right)$. Ta có:

$\sin \alpha =\cos \beta ;\cos \alpha =\sin \beta ;$$\tan \alpha =\cot \beta ;\cot \alpha =\tan \beta$

Trả lời:

$\tan {40}^o=\cot {50}^o$

Dấu cần điền vào chỗ trống là dấu $=.$

a) sin x = 1,010 ?                     b) cos x = 2,354 ?                    c) tan x = 1,675 ?

Nếu có, hãy dùng bảng số hoặc máy tính bỏ túi để tìm x ( làm tròn đến phút)

Phương pháp giải:

a; b) Vận dụng kiến thức : Cho góc nhọn $\alpha$. Ta có:

$0<\sin \alpha <1;0<\cos \epsilon <1;$${\sin }^2\alpha +{\cos }^2\alpha =1$

$\tan \alpha ={\displaystyle \frac{\sin \alpha }{\cos \alpha }};$$\cot \alpha ={\displaystyle \frac{\cos \alpha }{\sin \alpha }};\tan \alpha .\cot \alpha =1$

c) Dùng máy tính bỏ túi hoặc bảng số để tìm giá trị của x. 

Trả lời:

a) Vì với mọi góc nhọn $\alpha$, ta đều có $0<\sin \alpha <1$ nên không có góc nhọn x nào mà $\sin x=1,010.$

b) Vì với mọi góc nhọn $\alpha$, ta đều có $0<\cos \alpha <1$ nên không có góc nhọn x nào mà $\cos x=2,354.$

c) $\tan \mathrm{x}=1,675$ suy ra $x\approx {59}^o{9}^{\prime }$

a) $\sin {20}^0$ và $\sin {70}^0$ ;   

b) $\cos {25}^0$ và $\cos {63}^0{15}^{\prime }$ ;

c) $\tan {73}^0{20}^{\prime }$ và $\tan {45}^0$ ;

d) $\cot 2^0$ và $\cot {37}^0{40}^{\prime }$ .

Phương pháp giải:

Vận dụng kiến thức : Khi góc $\alpha$ tăng từ $0^o$ đến ${90}^o\left(0^o<\alpha <{90}^o\right)$ thì $\sin \alpha$ và $\tan \alpha$ tăng còn $\cos \alpha$ và $\cot \alpha$ giảm.

Trả lời:

Ta có : Khi $\alpha$ tăng từ $0^o$ đến ${90}^o$ thì $\sin \alpha$ và $\tan \alpha$ tăng còn $\cos \alpha$ và $\cot \alpha$ giảm. Bởi vậy :

a) $\sin {20}^o<\sin {70}^o$

b) $\cos {25}^o>\cos {63}^o{15}^{\prime }$

c) $\tan {73}^o{20}^{\prime }>\tan {45}^o$

d) $\cot 2^o>\cot {37}^o{40}^{\prime }$

Tam giác ABC vuông tại A, có $AC={\displaystyle \frac{1}{2}}BC$ . Tính sinB, cosB, tanB, cotB.

Phương pháp giải:

- Quy ước các đơn vị và dựa vào định nghĩa các tỉ số lượng giác trong tam giác vuông, tìm độ lớn của $\hat{B}.$

- Từ đó tính tiếp các giá trị lượng giác khác của $\hat{B}.$

Trả lời: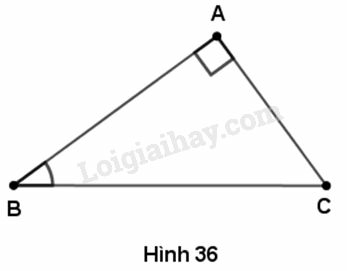

Trong tam giác vuông $ABC,$ nếu coi $AC=1$ thì $BC=2$ và ta có $\sin B={\displaystyle \frac{AC}{BC}}={\displaystyle \frac{1}{2}}$

Suy ra $\hat{B}={30}^o$

Từ bảng lượng giác của các góc đặc biệt, ta có :

$\cos B=\cos {30}^o={\displaystyle \frac{\sqrt{3}}{2}}$

$\tan B=\tan {30}^o={\displaystyle \frac{\sqrt{3}}{3}}$ 

$\cot B=\cot {30}^o=\sqrt{3}$

a) ${\displaystyle \frac{\sin {25}^0}{\cos {65}^0}};$

b) $\tan {58}^0-\cot {32}^0$ .

Phương pháp giải:

Vận dụng kiến thức : Cho hai góc $\alpha$ và $\beta$ phụ nhau $\left(\alpha +\beta ={90}^o\right)$. Ta có: 

$\sin \alpha =\cos \beta ;\cos \alpha =\sin \beta ;$$\tan \alpha =\cot \beta ;\cot \alpha =\tan \beta .$

Trả lời:

a) Vì hai góc ${25}^o$ và ${65}^o$ là hai góc phụ nhau nên $\sin {25}^o=\cos {65}^o,$ do đó :

${\displaystyle \frac{\sin {25}^o}{\cos {65}^o}}={\displaystyle \frac{\cos {65}^o}{\cos {65}^o}}=1.$

b) Vì hai góc ${58}^o$ và ${32}^o$ là hai góc phụ nhau nên $\tan {58}^o=\cot {32}^o,$ do đó :

$\tan {58}^o-\cot {32}^o$$=\cot {32}^o-\cot {32}^o=0.$

Bài 24 trang 96 Vở bài tập toán 9 tập 1:Hãy sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần :

a) $\sin {78}^0,cos{14}^0,\sin {47}^0,cos{87}^0;$

b) $\tan {73}^o,\cot {25}^o,\tan {62}^o,\cot {38}^o$ 

Phương pháp giải:

Vận dụng kiến thức :

-  Cho hai góc $\alpha$ và $\beta$ phụ nhau $\left(\alpha +\beta ={90}^o\right)$. Ta có:

$\sin \alpha =\cos \beta ;\cos \alpha =\sin \beta ;$$\tan \alpha =\cot \beta ;\cot \alpha =\tan \beta .$

- Khi góc $\alpha$ tăng từ $0^o$ đến ${90}^o\left(0^o<\alpha <{90}^o\right)$ thì $\sin \alpha$ và $\tan \alpha$ tăng còn $\cos \alpha$ và $\cot \alpha$ giảm để so sánh các góc rồi sắp xếp theo thứ tự tăng dần.

Trả lời:

a) Ta có : $\cos {14}^o=\sin \left({90}^o-{14}^o\right)=\sin {76}^o$

                 $\cos {87}^o=\sin \left({90}^o-{87}^o\right)=\sin 3^o$

Và $3^o<{47}^o<{76}^o<{78}^o$

Vì khi $\alpha$ tăng từ $0^o$ đến ${90}^o\left(0^o<\alpha <{90}^o\right)$ thì $\sin \alpha$tăng nên ta có :

$\sin 3^o<\sin {47}^o<\sin {76}^o<\sin {78}^o$

Bởi vậy $\cos {87}^o<\sin {47}^o<\cos {14}^o<\sin {78}^o$.

b) Ta có : $\cot {25}^o=\tan \left({90}^o-{25}^o\right)=\tan {65}^o$

$\cot {38}^o=\tan \left({90}^o-{38}^o\right)=\tan {52}^o$

Và ${52}^o<{62}^o<{65}^o<{73}^o$

Vì khi $\alpha$ tăng từ $0^o$ đến ${90}^o\left(0^o<\alpha <{90}^o\right)$ thì $\tan \alpha$ giảm nên ta có :

$\tan {73}^o<\tan {65}^o<\tan {62}^o<\tan {52}^o$

Bởi vậy $\tan {73}^o<\cot {25}^o<\tan {62}^o<\cot {38}^o$.

a) sinx – 1

b) 1 – cosx

Phương pháp giải:

Vận dụng kiến thức : Với góc nhọn $\alpha$ ta có : $0<\sin \alpha <1;0<\cos \alpha <1$

Trả lời:

a) Vì với góc nhọn x bất kì, ta luôn có $0<\sin \mathrm{x}<1$ nên $\sin x-1<0.$

b) Vì với góc nhọn x bất kì, ta luôn có $0<\cos \mathrm{x}<1$ nên $1-\cos \mathrm{x}>0$

a) tan 25^o và sin25^o      

b) cot32^o và cos32^o

c) tan45^o và cos45^o

d) cot60^o và sin30^o

Phương pháp giải:

- Vận dụng kiến thức : Với góc nhọn $\alpha$ ta có :$\tan \alpha ={\displaystyle \frac{\sin \alpha }{\cos \alpha }};\cot \alpha ={\displaystyle \frac{\cos \alpha }{\sin \alpha }}$ và $0<\sin \alpha <1;0<\cos \alpha <1$.

- Khi chia số $a$ với một số nhỏ hơn (hoặc lớn hơn) $1$ thì được kết quả có giá trị lớn hơn (hoặc nhỏ hơn) $a$.

Trả lời

a) Vì $\tan {25}^o={\displaystyle \frac{\sin {25}^o}{\cos {25}^o}}$ mà $\cos {25}^o<1$ nên $\tan {25}^o>\sin {25}^o.$

b) Vì $\cot {32}^o={\displaystyle \frac{\cos {32}^o}{\sin {32}^o}}$ mà $\sin {32}^o<1$ nên $\cot {32}^o>\cos {32}^o.$

c) Vì $\tan {45}^o={\displaystyle \frac{\sqrt{2}}{2}}$ mà $\cos {45}^o<1$ nên $\tan {45}^o>\cos {45}^o.$

d) Vì $\cot {60}^o={\displaystyle \frac{\sqrt{3}}{3}}$ mà $\sin {30}^o={\displaystyle \frac{1}{2}}$ nên $\cot {60}^o>\sin {30}^o.$

Dùng bảng số hoặc máy tính để tính các góc của tam giác ABC, biết AB = 3cm, AC = 4cm, BC = 5cm (làm tròn đến phút).

Phương pháp giải:

- Dùng định lí Pi-ta-go đảo để kiểm tra tam giác $ABC$ là tam giác vuông hay chưa ?

- Nếu là tam giác vuông, em sử dụng định nghĩa các tỉ số lượng giác đã học để tìm độ lớn của ba góc trong tam giác.

Trả lời:

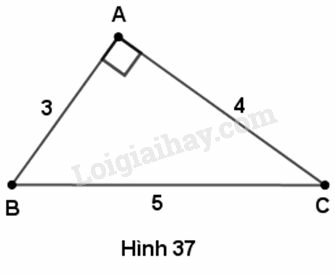
Trong tam giác $ABC$, ta có :

$A{B}^2+A{C}^2=3^2+4^2=5^2=B{C}^2.$

Do đó, theo định lí Pi-ta-go đảo, tam giác $ABC$ là tam giác vuông tại $A.$ Bởi vậy, theo định nghĩa các tỉ số lượng giác của một góc nhọn, ta có :

$\sin B={\displaystyle \frac{AC}{BC}}={\displaystyle \frac{4}{5}}=0,8\Rightarrow \hat{B}\approx {53}^o{7}^{\prime }.$

Từ đó suy ra $\hat{C}={90}^o-\hat{B}\approx {90}^o-{53}^o{7}^{\prime }={36}^o{3}^{\prime }.$