Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Ôn tập chương 1 - Hệ thức lượng trong tam giác vuông trang 105,106,107  chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:

VBT Toán lớp 9 Ôn tập chương 1 - Hệ thức lượng trong tam giác vuông

Bài 42 trang 105 Vở bài tập toán 9 tập 1: Cho tam giác có một góc bằng 45^o. Đường cao chia một cạnh kề với góc đó thành các phần 20cm và 21cm. Tính cạnh lớn hơn trong hai cạnh còn lại (lưu ý có hai trường hợp).

Phương pháp giải:

- Vẽ hình theo hai trường hợp.

- Dùng định lí Pi-ta-go so sánh độ dài hai cạnh và tính độ dài cạnh lớn hơn.

Trả lời:

1) Trường hợp 1 (h. 53) :

Tam giác $AHB$ vuông cân tại $H$ nên $AH=BH=20cm.$ Do đó :

$AB=\sqrt{{20}^2+{20}^2}<\sqrt{{20}^2+{21}^2}=AC.$

Vậy cạnh $AC$ là cạnh lớn và $AC=29\left(cm\right).$

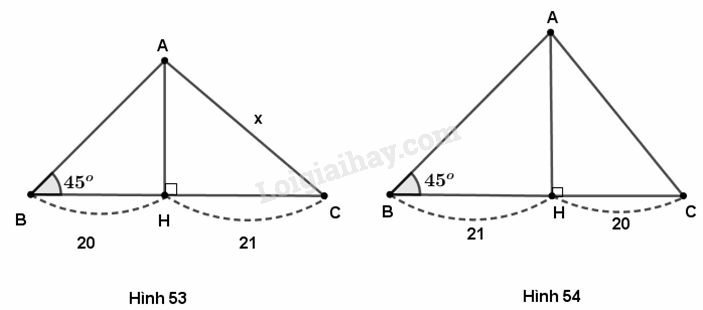
2) Trường hợp 2 (h.54) :

Tam giác AHB vuông cân tại $H$ nên $AH=BH=21cm.$ Do đó :

$AB=\sqrt{{21}^2+{21}^2}>\sqrt{{20}^2+{21}^2}=AC.$

Vậy cạnh $AB$ là cạnh lớn và $AB\approx 29,698\left(cm\right).$

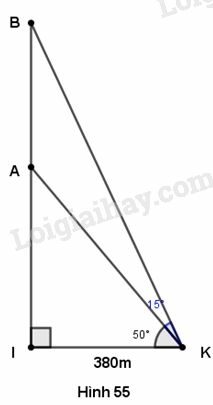
Tìm khoảng cách AB trong hình 55 (làm tròn đến mét). 

Phương pháp giải:

- Vận dụng kiến thức : Trong tam giác vuông, cạnh góc vuông bằng cạnh góc vuông kia nhân với tang góc đối để tìm độ dài cạnh $IB;IA.$

- Từ đó tính độ dài cạnh $AB.$

Trả lời:

Trong tam giác vuông $BIK,$ có $\hat{K}={50}^o+{15}^o={65}^o$ và $IB=IK.\tan \widehat{IKB}$$=380.\tan {65}^o\approx 815\left(m\right).$

Trong tam giác vuông $AIK,$ có $AI=IK.\tan \widehat{IKA}$$=380.\tan {50}^o\approx 453\left(m\right).$

Vậy khoảng cách $AB$ là:

$AB=IB-IA$$\approx 815-453=362\left(m\right).$

Từ một đỉnh ngọn đèn biển cao 38m so với mặt nước biển, người ta nhìn thấy một hòn đảo dưới góc 30^o so với đường nằm ngang chân đèn. Hỏi khoảng cách từ đảo đến chân đèn (ở mực nước biển) bằng bao nhiêu ? (làm tròn đến mét).

Phương pháp giải:

Vận dụng kiến thức : Trong tam giác vuông, cạnh góc vuông bằng cạnh góc vuông kia chia cho tang góc kề.

Trả lời:

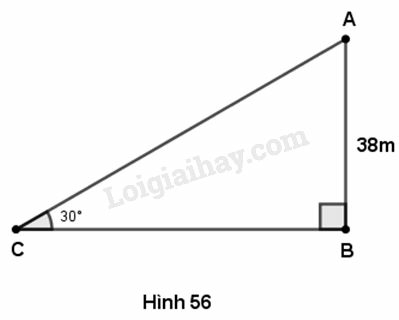
Trong hình 56, giả sử $A$ là đỉnh của ngọn đèn biển, $B$ là chân đèn (ở mực nước biển) và $C$ là vị trí hòn đảo mà người quan sát nhìn thấy từ $A.$ Trong tam giác vuông $ABC,$ ta có :

$BC={\displaystyle \frac{AB}{\tan \widehat{ACB}}}$$={\displaystyle \frac{38}{\tan {30}^o}}\approx 66\left(m\right).$

Vậy khoảng cách từ đảo đến chân đèn (ở mực nước biển) vào khoảng $66m.$

Cho tam giác ABC có AB = 6m, AC = 4,5cm, BC = 7,5cm

a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH (làm tròn đến chữ số thập phân thứ hai).

b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nằm trên đường nào ?

Phương pháp giải:

a) Áp dụng định lí Pi-ta-go đảo : Tam giác có tổng bình phương hai cạnh bằng bình phương cạnh kia thì tam giác đó là tam giác vuông để chứng minh.

    Áp dụng tỉ số lượng giác $\sin \alpha ={\displaystyle \frac{\text{cạnh đối}}{\text{cạnh huyền}}}$ để tìm độ lớn của góc $B.$

    Tính độ lớn góc $C$ bằng cách $\hat{C}={90}^o-\hat{B}.$ 

    Tính đường cao $AH$ bằng cạnh huyền $AB$ nhân với $\sin$ góc đối.

b) Để $S_{ABC}=S_{MBC}$ thì cặp cạnh đáy và chiều cao tương ứng của hai tam giác bằng nhau.

Trả lời:

a) Tam giác $ABC$ có :

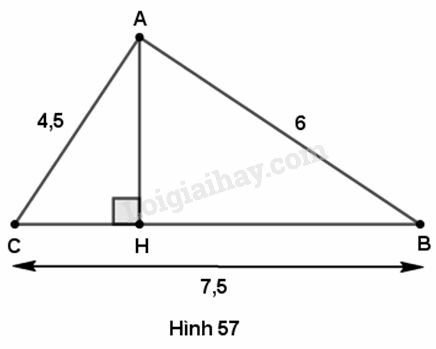
$A{B}^2+A{C}^2=6^2+4,5^2$$=7,5^2=B{C}^2.$

Vậy tam giác $ABC$ là tam giác vuông tại $A.$

Do đó, $\sin B={\displaystyle \frac{AC}{BC}}$$=4,5:7,5=0,6$

Suy ra $\hat{B}\approx {36}^o{52}^{\prime }$ và $\hat{C}\approx {90}^o-{36}^o{52}^{\prime }$$={53}^o{8}^{\prime }.$

Trong tam giác vuông $AHB$ có

$AH=AB.\sin B=6.0,6=3,6\left(cm\right).$

b) $S_{MBC}=S_{ABC}$ khi đường cao kẻ từ $M$ của tam giác $MBC$ bằng $AH.$ ( Do tam giác ABC và MBC có chung đáy BC). Từ đó suy ra $M$ nằm trên hai đường thẳng song song với $BC$ và cùng cách $BC$ một khoảng $3,6cm.$

Bài 46 trang 107 Vở bài tập toán 9 tập 1:Cho hình 58. Tính khoảng cách AD (làm tròn đến chữ số thập phân thứ hai).

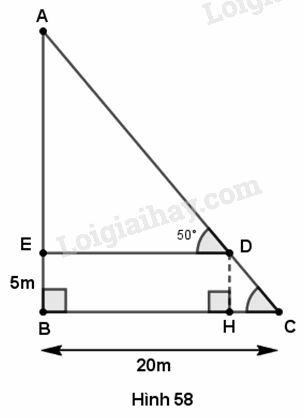
Phương pháp giải:

- Tìm độ dài cạnh huyền$AC$ bằng cách lấy cạnh $BC$ chia cho cos góc kề.

- Tìm độ dài cạnh huyền $DC$ bằng cách lấy cạnh góc vuông $DH$ chia cho $\sin$ góc kề.

- Từ đó tìm độ dài cạnh $AD.$

Trả lời:

Trong tam giác vuông $ABC,$ ta có :

$\hat{C}=\widehat{ADE}={50}^o$ và $AC={\displaystyle \frac{BC}{\cos C}}={\displaystyle \frac{20}{\cos {50}^o}}\approx 31,11\left(m\right).$

Trong tam giác vuông $DHC,$ ta có :

$DH=EB=5m$ và $DC={\displaystyle \frac{DH}{\sin C}}={\displaystyle \frac{5}{\sin {50}^o}}\approx 6,53\left(m\right).$

Vậy khoảng cách $AD$ là: 

$AD=AC-DC\approx 31,11-6,53$$=24,58\left(m\right).$