Toptailieu.vn xin giới thiệu 40 bài tập trắc nghiệm Ôn tập chương 1 (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 9 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.
Mời các bạn đón xem:
Ôn tập chương 1
Câu 1: Cho tam giác ABC vuông tại A, chiều cao AH. Chọn câu sai.
Lời giải:
Ta thấy AH. BC = AB. AC nên D sai
Đáp án cần chọn là: D
Câu 2: Cho hình vẽ sau:
Chọn câu sai.
Lời giải:
Đáp án cần chọn là: D
Câu 3: Chọn câu đúng nhất. Nếu α là một góc nhọn bất kì, ta có:
Lời giải:
Nếu α là một góc nhọn bất khì thì sin2α + cos2α = 1; tanα . cotα = 1;
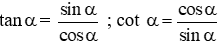
Đáp án cần chọn là: D
Câu 4: Cho α; β là hai góc nhọn bất kì α < β. Chọn câu đúng.
A. sinα > sinβ.
B. cosα < cosβ.
C. tanα < tanβ.
D. cotα < cotβ.
Lời giải:
Với α; β là hai góc nhọn bất kì và α < β thì
sinα < sinβ ; cosα > cosβ ; tanα < tanβ ; cotα > cotβ.
Vậy A, B, D sai, C đúng
Đáp án cần chọn là: C
Câu 5: Tính giá trị của x trên hình vẽ:
Lời giải:
Xét tam giác MNP vuông tại M, có MK ⊥ NP ta có MK2 = NK.PK (hệ thức lượng trong tam giác vuông)
Hay x2 = 6.9 ⇔ x2 = 54 ⇒ x = 3√6
Đáp án cần chọn là: C
Câu 6: Cho tan a = 3. Khi đó cot a bằng?
Lời giải:
Đáp án cần chọn là: A
Câu 7: Cho tam giác ABC vuông tại A có AB = 3cm, BC = 5cm. AH là đường cao. Tính BH, CH, AC và AH.
A. BH = 2cm, CH = 3,2cm, AC = 4cm, AH = 2,4cm
B. BH = 1,8cm; CH = 3,2cm; AC = 4cm; AH = 2,4cm
C. BH = 1,8cm; CH = 3,2cm; AC = 3cm; AH = 2,4cm
D. BH = 1,8cm; CH = 3,2cm; AC = 4cm; AH = 4,2cm
Lời giải:
Xét tam giác ABC vuông tại A
+ Theo định lý Pytago ta có AB2 + AC2 = BC2 ⇔ AC2 = 52 – 32 ⇒ AC = 4cm
+ Theo hệ thức lượng trong tam giác vuông ta có:
Vậy BH = 1,8cm, CH = 3,2cm, AC = 4cm, AH = 2,4 cm
Đáp án cần chọn là: B
Câu 8: Giải tam giác vuông ABC, biết 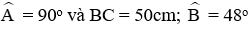
Lời giải:
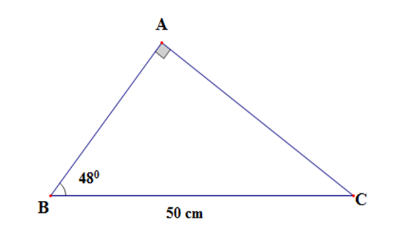
Áp dụng hệ thức liên hệ giữa cạnh và góc trong tam giác vuông ta có:
AC = BC. sin B = 50. sin 48o ≈ 37,2cm
AB = BC. cos B = 50. cos 48o ≈ 33,5cm
Đáp án cần chọn là: D
Câu 9: Cho tam giác ABC vuông tại A có 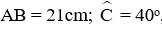
A. 21,3 cm
B. 24 cm
C. 22,3 cm
D. 23,2 cm
Lời giải:
Đáp án cần chọn là: D
Câu 10: Cho tam giác ABC vuông tại A, có AC = 14, BC = 17. Khi đó tan B bằng:
Lời giải:
Xét tam giác ABC vuông tại A, theo định lý Py-ta-go ta có:
Đáp án cần chọn là: C
Câu 11: Giá trị biểu thức sin4α + cos4α + 2 sin2α . cos2α là?
A. 1
B. 2
C. 4
D. −1
Lời giải:
Đáp án cần chọn là: A
Câu 12: Cạnh bên của tam giác ABC cân tại A dài 20cm, góc ở đáy là 50o. Độ dài cạnh đáy của tam giác cân là? (kết quả làm tròn đến chữ số thập phân thứ nhất).
A. 25cm
B. 25,7cm
C. 26cm
D. 12,9cm
Lời giải:
Kẻ AH ⊥ BC tại H. Suy ra H là trung điểm BC (do tam giác ABC cân tại A có AH vừa là đường cao vừa là đường trung tuyến)
Đáp án cần chọn là: B
Câu 13: Cho hình vẽ, tìm x.
A. x = 0,75
B. x = 4,5
C. x = 4√3
D. x = 4
Lời giải:
Đặt tên như hình vẽ trên.
Tam giác MNP vuông tại M có MH ⊥ NP
Theo hệ thức lượng trong tam giác vuông ta có:
MN2 = NH. NP ⇒ 62 = x.8 ⇒ x = 36 : 8 = 4,5
Vậy x = 4,5
Đáp án cần chọn là: B
Câu 14: Cho
Lời giải:
Vì 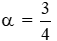
Đáp án cần chọn là: A
Câu 15: Tìm x; y trong hình vẽ sau:
Lời giải:
Ta có: BC = BH + HC = y + 32
Áp dụng hệ thức lượng AB2 = BH.BC trong tam giác vuông ABC ta có:
Suy ra y = 18 ⇒ BC = 18 + 32 = 50
Áp dụng hệ thức lượng AC2 = CH.BC ta có:
x2 = 32.50 ⇔ x2 = 1600 ⇒ x = 40
Vậy c = 40; y = 18
Đáp án cần chọn là: D
Câu 16: Tính số đo góc nhọn x, biết cos2x – sin2x =
A. 45o
B. 30o
C. 60o
D. 90o
Lời giải:
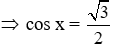
Suy ra x = 30o
Đáp án cần chọn là: B
Câu 17: Cho ΔABC vuông tại A. Biết 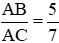
Lời giải:
Theo hệ thức lượng trong tam giác ABC vuông tại A ta có:
Đáp án cần chọn là: D
Câu 18: Cho ABC vuông tại A, AB = 12cm, AC = 16cm, tia phân giác AD, đường cao AH. Tính HD.
Lời giải:
Xét tam giác vuông ABC ta có BC2 = AB2 + AC2 (định lý Py-ta-go)
Hay BC2 = 122 + 162 ⇒ BC2 = 400 ⇒ BC = 20cm
Vì AD là phân giác góc A nên theo tính chất đường phân giác trong tam giác ta có:
Theo hệ thức lượng trong tam giác vuông ABC ta có:
Đáp án cần chọn là: A
Câu 19: Tính giá trị C = (3sinα + 4 cosα)2 + (4sinα − 3 cosα)2
A. 25
B. 16
C. 9
D. 25 + 48sinα.cosα
Lời giải:
Ta có C = (3sinα + 4 cosα)2 + (4sinα − 3 cosα)2
= 9sin2α + 24 sin .cos + 16cos2α + 16sin2α − 24 sinα.cosα + 9cos2α
= 25sin2α + 25 cos2α = 25 (sin2α + cos2α) = 25.1 = 25
Vậy C = 25
Đáp án cần chọn là: A
Câu 20: Cho biết 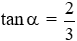
Lời giải:
Chia cả từ và mẫu của M cho cos3α ta được:
Đáp án cần chọn là: D
Câu 21: Cho hình vẽ sau:
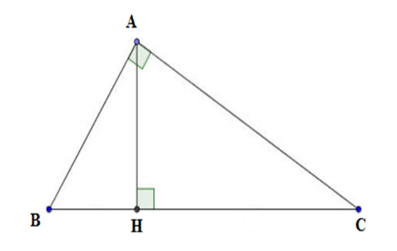
Chọn câu sai.
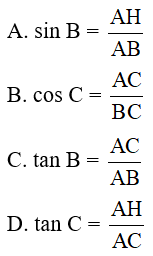
Lời giải:
+ Xét tam giác AHB vuông tại H
có sin B = nên A đúng.
+ Xét tam giác ABC vuông tại A có
cos C = nên B đúng.
+ Xét tam giác ABC vuông tại A
có tan B = nên C đúng.
+ Xét tam giác AHC vuông tại H
có tan C = nên D sai
Đáp án cần chọn là:D
Câu 22: Sắp xếp theo thứ tự tăng dần:
cot 70o, tan 33o, cot 55o, tan 28o, cot 40o
A. tan 28o < tan 33o < cot 40o < cot 55o < cot 70o
B. tan 28o < cot 70o < tan 33o < cot 55o < cot 40o
C. cot 70o < tan 28o < tan 33o < cot 55o < cot 40o
D. cot 70o > tan 28o > tan 33o cot 55o >cot 40o
Lời giải:
Ta có: cot70o = tan20o vì 70o + 20o = 90o;
cot 55o = tan35o vì 55o + 35o = 90o;
cot 40o = tan 50o vì 40o + 50o = 90o
Lại có 20o < 28o < 33o < 35o < 50o
Hay tan 20o < tan 28o < tan 33o < tan 35o < tan 50o
Suy ra cot 70o < tan 28o < tan 33o < cot 55o < cot 40o
Đáp án cần chọn là:C
Câu 23: Cho tam giác ABC vuông tại A có AB = 3cm, BC = 5cm. AH là đường cao. Tính BH, CH, AC và AH.
A. BH = 2cm, CH = 3,2cm, AC = 4cm, AH = 2,4cm
B. BH = 1,8cm; CH = 3,2cm; AC = 4cm; AH = 2,4cm
C. BH = 1,8cm; CH = 3,2cm; AC = 3cm; AH = 2,4cm
D. BH = 1,8cm; CH = 3,2cm; AC = 4cm; AH = 4,2cm
Lời giải:
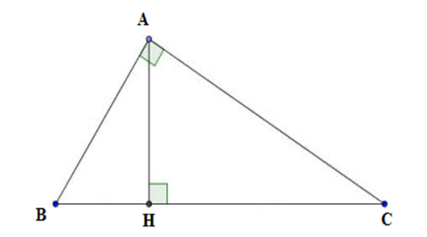
Xét tam giác ABC vuông tại A
+ Theo định lý Pytago ta có AB2 + AC2 = BC2
AC2 = 52 – 32 AC = 4cm
+ Theo hệ thức lượng trong tam giác vuông ta có:
AB2 = BH. BC
BH =
Mà BH + CH = BC
CH = BC – BH = 5 – 1,8 = 3,2 cm
Lại có AH. BC = AB.AC
AH = = 2,4cm
Vậy BH = 1,8cm, CH = 3,2cm,
AC = 4cm, AH = 2,4 cm
Đáp án cần chọn là:B
Câu 24: Cho tam giác ABC vuông tại A, chiều cao AH. Chọn câu sai.
A. AH2 = BH. CH
B. AB2 = BH. BC
C.
D. AH. AB = BC. AC
Lời giải:
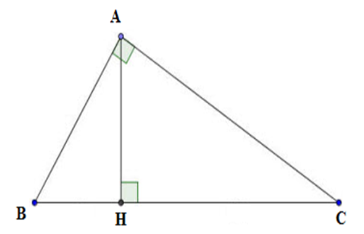
Ta thấy AH. BC = AB. AC nên D sai
Đáp án cần chọn là:D
Câu 25: Tìm x; y trong hình vẽ sau:
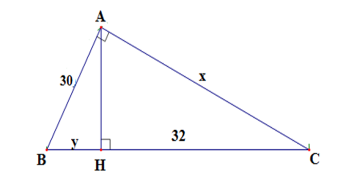
A. x = 30; y = 28
B. x = 2; y =
C. x = 18; y = 40
D. x = 40; y = 18
Lời giải:
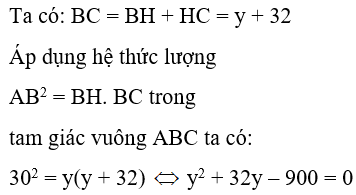
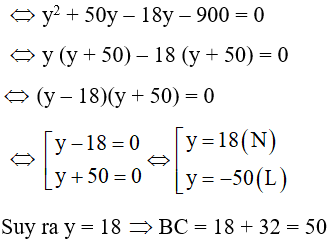

Câu 26: Cho tan a = 3. Khi đó cota bằng?
A.
B. 3
C.
D.
Lời giải:
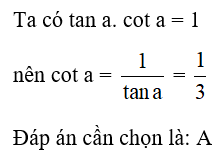
Câu 27: Giải tam giác vuông ABC, biết = 90ovà BC = 50cm; = 48o (làm tròn đến chữ số thập phân thứ nhất).

Lời giải:
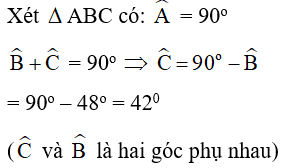

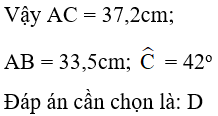
Câu 28: Chọn câu đúng nhất. Nếu là một góc nhọn bất kì, ta có:
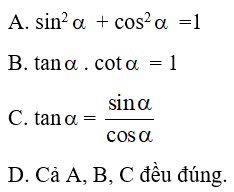
Lời giải:

Câu 29: Tính giá trị của x trên hình vẽ:
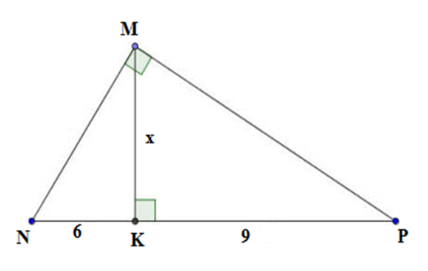
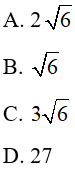
Lời giải:
Xét tam giác MNP vuông tại M,
có MKNP ta có MK2 = NK.PK
(hệ thức lượng trong tam giác vuông)
Hay x2 = 6.9x2 = 54x =3
Đáp án cần chọn là:C
Câu 30: Tính giá trị
C = (3sin + 4 cos )2 + (4sin − 3 cos)2
A. 25
B. 16
C. 9
D. 25 + 48sin.cos
Lời giải:
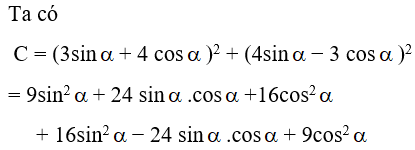
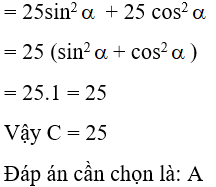
Câu 31: Cho ABC vuông tại A có đường cao AH và đường trung tuyến AM. Biết AH = 3cm; HB = 4cm. Hãy tính AB, AC, AM và diện tích tam giác ABC.
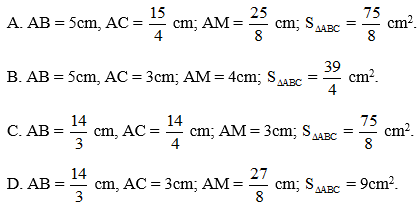
Lời giải:
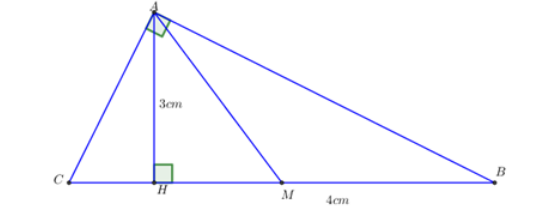




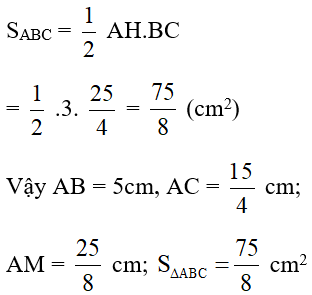
Đáp án cần chọn là:A
Câu 32: Cho biết tan =. Tính giá trị biểu thức:
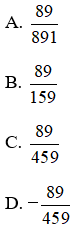
Lời giải:
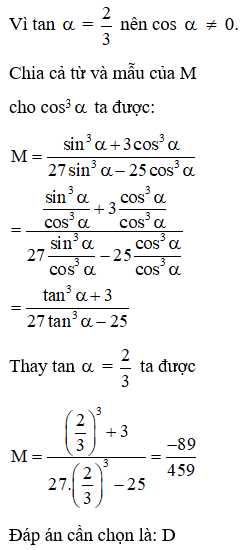
Câu 33: Cho đoạn thẳng AB = 2a và trung điểm O của nó. Trên nửa mặt phẳng bờ AB vẽ các tia Ax, By vuông góc với AB. Qua O vẽ một tia cắt Ax tại M sao cho < 90o. Qua O vẽ tia thứ hai cắt By tại N sao cho = 90o. Khi đó, diện tích tam giác MON là:
Lời giải:
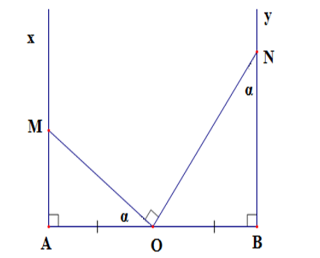

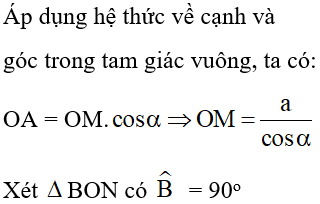

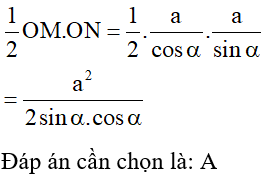
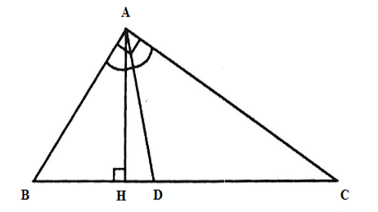
Câu 34: Cho ABC vuông tại A, AB = 12cm, AC = 16cm, tia phân giác AD, đường cao AH. Tính HD.
Lời giải:



Câu 35: Cho tam giác ABC có diện tích là 900cm2. Điểm D ở giữa BC sao cho BC = 5DC, điểm E ở giữa AC sao cho AC = 4AE, hai điểm F, G ở giữa BE sao cho BE = 6GF = 6GE. Tính diện tích tam giác DGF.
A. 80cm2
B. 90cm2
C. 100cm2
D. 120cm2
Lời giải:
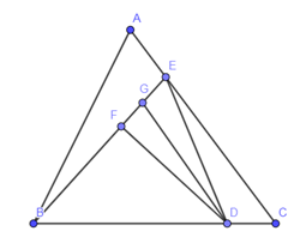
Ta kí hiệu d(A; BC) là khoảng cách từ A đến đường thẳng BC (nghĩa là độ dài đoạn vuông góc kẻ từ A đến BC), tương tự với những kí hiệu khác trong bài.
Ta có:
Đáp án cần chọn là:B
Câu 36: Tính x, y trong hình vẽ sau:
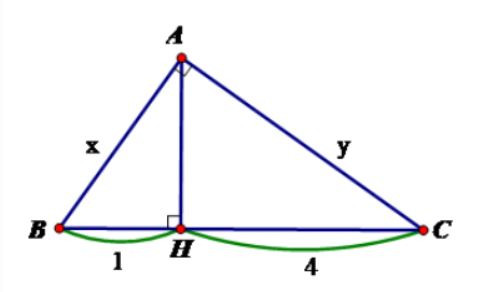
A. x = 2, y =
B. x= , y =
C. x = , y = 2
D. x = 2, y = 2
Lời giải:
Áp dụng hệ thức giữa cajnh và đường cao trong tam giác vuông ta có:
AH2 = BH.CH AH2 = 1,4 AH = 2
Áp dụng định lý Pytago cho tam giác vuông ta có:
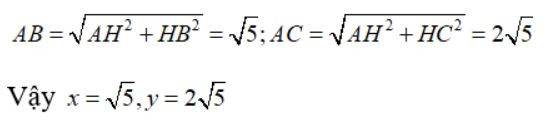
Đáp án cần chọn là:C
Câu 37: Tính x trong hình vẽ sau(làm tròn đến chữ số thập phân thứ hai)

A. X 8.81
B. x 8.82
C. x 8.83
D. x 8.80
Lời giải:
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ABC ta có:

Đáp án cần chọn là:B
Câu 38: Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB:AC = 3:4 và AH = 6cm. Tính độ dài đoạn thẳng CH.
A. CH = 8cm
B. CH = 6cm
C. CH = 10cm
D. CH = 12cm
Lời giải:
Ta có: AB:AC = 3:4, đặt AB = 3a; AC = 4a(a>0)
Theo hệ thức về cạnh và đường cao trong tam giác vuông AHC ta có:
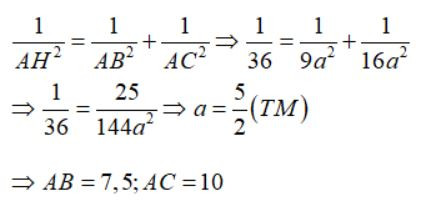
Theo định lý Pytago cho tam giác vuông ta có:
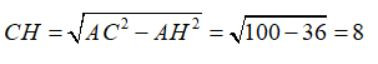
Đáp án cần chọn là:A
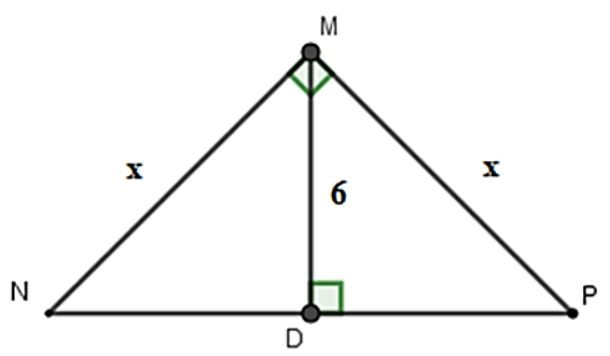
Câu 39: Tính x trong hình vẽ sau:
A. x =
B. x = 6
C. x = 6
D. x =
Lời giải:
Áp dụng hệ thức lượng giữa cạnh và đường cao trong tam giác vuông ta có:
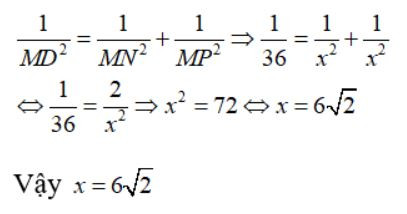
Đáp án cần chọn là:A
Câu 40: Cho tam giác ABC vuông tại C có BC = 1,2cm; AC = 0,9cm. Tính tỉ số lượng giác sinB; cosB
A. sinB = 0,6; cosB = 0,8
B. sinB = 0,8; cosB = 0,6
C. sinB = 0,4; cosB = 0,8
D. sinB = 0,6; cosB = 0,4
Lời giải:
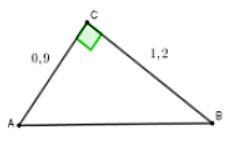

Đáp án cần chọn là:A
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.