Toptailieu.vn xin giới thiệu 50 bài tập trắc nghiệm  Liên hệ giữa dây và khoảng cách từ tâm đến dây (có đáp án) chọn lọc, hay nhất giúp học sinh lớp 9 ôn luyện kiến thức để đạt kết quả cao trong các bài thi môn Toán.

Mời các bạn đón xem:

Liên hệ giữa dây và khoảng cách từ tâm đến dây

Câu 1: Cho đường tròn (O) có hai dây AB, CD không đi qua tâm. Biết khoảng cách từ tâm đến hai dây là bằng nhau. Kết luận nào sau đây là đúng?

A. AB > CD

B. AB = CD

C. AB < CD

D. AB // CD

Lời giải:

Trong một đường tròn, hai dây cách đều tâm thì bằng nhau

Đáp án cần chọn là:B

Câu 2: Cho đường tròn (O) có bán kính R = 5cm. Khoảng cách từ tâm đến dây AB là 3cm. Tính độ dài dây AB.

A. AB = 6cm

B. AB = 8cm

C. AB = 10cm

D. AB = 12cm

Lời giải:

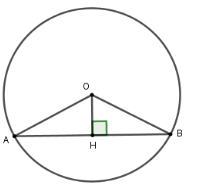
Kẻ OHAB tại H suy ra H là trung điểm AB

Xét tam giác OHB vuông tại H

có OH = 3cm;OB = 5cm.

Theo định lý Pytago ta có:

HB = $\sqrt{O{B}^2-O{H}^2}=\sqrt{5^2-3^2}$ = 4

Mà H là trung điểm của AB

nên AB = 2HB = 8cm

Vậy AB = 8cm

Đáp án cần chọn là:B

Câu 3: Chọn khẳng định đúng trong các khẳng định sau. Trong hai dây của một đường tròn.

A. Dây nào lớn hơn thì dây đó xa tâm hơn

B. Hai dây đi qua tâm thì vuông góc với nhau

C. Dây nào gần tâm hơn thì dây đó nhỏ hơn

D. Hai dây cách đều tâm thì bằng nhau

Lời giải:

- Trong một đường tròn:

+ Hai dây bằng nhau thì cách đều tâm

- Trong hai dây của một đường tròn:

+ Dây nào lớn hơn thì dây đó gần tâm hơn

+ Dây nào gần tâm hơn thì dây đó lớn hơn

Nên phương án A, B, C sai; D đúng

Đáp án cần chọn là:D

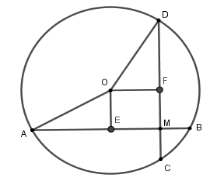
Câu 4: Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết AB = 16cm; CD = 12cm; MC = 2cm. Khoảng cách từ tâm O đến dây AB là?

A. 4cm

B. 5cm

C. 3cm

D. 2cm

Lời giải:

Câu 5: Chọn khẳng định sai trong các khẳng định sau. Trong hai dây của một đường tròn.

A. Dây nào lớn hơn thì dây đó xa tâm hơn

B. Dây nào nhỏ hơn thì dây đó xa tâm hơn

C. Dây nào gần tâm hơn thì dây đó lớn hơn

D. Hai dây bằng nhau thì cách đều tâm

Lời giải:

- Trong một đường tròn:

+ Hai dây bằng nhau thì cách đều tâm

- Trong hai dây của một đường tròn:

+ Dây nào lớn hơn thì dây đó gần tâm hơn

+ Dây nào gần tâm hơn thì dây đó lớn hơn

Nên phương án B, C, D đúng

Đáp án cần chọn là:A

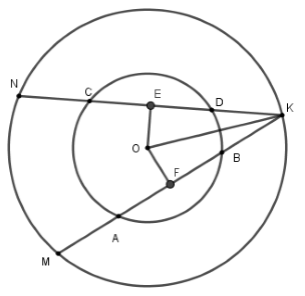
Câu 6: Cho đường tròn (O), dây cùng AB và CD với CD = AB. Giao điểm K của các đường thẳng AB và CD nằm ngoài đường tròn. Vẽ đường tròn (O; OK), đường tròn này cắt KA và KC lần lượt tại M và N. So sánh KM và KN.

A. KN > KM 

B. KN < KM

C. KM = KN

D. KN =  KM

Lời giải:

Câu 7: Cho đường tròn (O) có bán kính R = 6,5cm. Khoảng cách từ tâm đến dây AB là 2,5cm. Tính độ dài dây AB.

A. AB = 6cm

B. AB = 8cm

C. AB = 10cm

D. AB = 12cm

Lời giải:

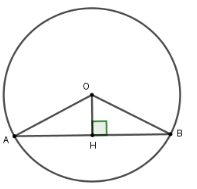
Kẻ OHAB tại H suy ra H là trung điểm AB

Xét tam giác OHB vuông tại H

có OH = 2,5cm; OB = 6,5cm.

Theo định lý Pytago ta có:

HB = $\sqrt{O{B}^2-O{H}^2}=\sqrt{6,5^2-2,5^2}$ = 6

Mà H là trung điểm của AB

nên AB = 2HB = 12cm

Vậy AB = 12cm

Đáp án cần chọn là:D

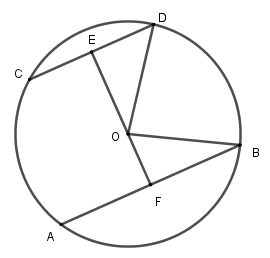
Câu 8: Cho đường tròn (O; R) có hai dây AB, CD bằng nhau và vuông góc với nhau tại I. Giả sử IA = 2cm; IB = 4cm. Tổng khoảng cách từ tâm O đến dây AB, CD là:

A. 4cm

B. 1cm 

C. 3cm

D. 2cm

Lời giải:

Xét đường tròn tâm (O).

Kẻ OE$\perp$AB tại E suy ra E là trung điểm của AB,

kẻ OFCD tại F.

Vì dây AB = AC nên OE = OF

(hai dây bằng nhau cách đều tâm)

Xét tứ giác OEIF có $\widehat{E}=\widehat{F}=\widehat{I}$ = 90^o

nên OEIF là hình chữ nhật và OE = OF

nên OEIF là hình vuông

$\Rightarrow$ OE = OF = EI

Mà AB = IA + IB = 6cm

$\Rightarrow$EB = 3cm EI = EB – IB = 1cm

nên OE = OF = 1cm

Vậy tổng khoảng cách từ tâm đến hai dây là AB, CD là 2cm

Đáp án cần chọn là:D

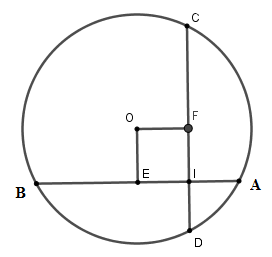
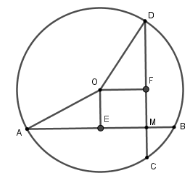
Câu 9: Cho đường tròn (O; 8cm). Dây AB và CD song song, có độ dài lần lượt là 14cm và 10cm. Tính khoảng cách giữa 2 dây.

Lời giải:

Kẻ đường thẳng qua O vuông góc với CD tại E và cắt AB tại F thì EF  AB vì AB // CD

Khi đó E là trung điểm của CD và F là trung điểm của AB (đường kính vuông góc với dây thì đi qua trung điểm dây đó).

Nên ED = $\frac{CD}{2}$ = 5cm;

FB = $\frac{AB}{2}$ = 7cm; OD = OB = 8cm

Áp dụng định lý Pytago cho tam giác vuông OED ta được:

OE = $\sqrt{O{D}^2-E{D}^2}$ = $\sqrt{8^2-5^2}$= $\sqrt{39}$ cm

Áp dụng định lý Pytago cho tam giác vuông OFB ta được:

OF =$\sqrt{O{B}^2-F{B}^2}$=$\sqrt{8^2-7^2}$ = $\sqrt{15}$ cm

Vậy khoảng cách giữa hai dây

là EF = OE + OF =$\sqrt{39}+\sqrt{15}$(cm)

Đáp án cần chọn là:D

Câu 10: Cho đường thẳng d cắt đường tròn (O) tại hai điểm phân biệt A, B. Biết khoảng cách từ điểm O đến đường thẳng d bằng 3cm và độ dài đoạn thẳng AB bằng 8cm. Bán kính của đường tròn (O) bằng:

A. 7cm

B. 11cm

C. 73cm

D. 5cm

Lời giải:

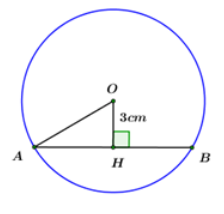
Kẻ OH$\perp$AB. Khi đó H là trung điểm của AB (mối liên hệ giữa đường kính và dây cung)  

$\Rightarrow \left\{\begin{array}{l}OH=3cm\\ AH=\frac{1}{2}AB=4cm\end{array}\right.$

Áp dụng định lý Pytago cho $\Delta$AOH vuông tại H ta có:

OA² = AH² + HO² = 4² + 3² = 25  

$\Rightarrow$R = OA = 5cm

Đáp án cần chọn là:D

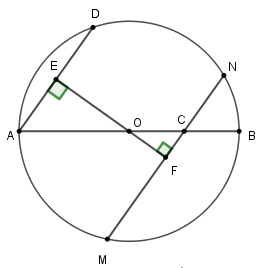
Câu 11: Cho đường tròn (O), đường kính AB. Lấy điểm C là trung điểm đoạn OB. Kẻ dây MN qua C và dây AD//MN. So sánh độ dài AD và MN

A. AD = 2.MN 

B. AD = MN

C. AD > MN 

D. AD < MN

Lời giải:

Câu 12: Cho đường tròn (O), đường kính AB. Kẻ hai dây AC và BD song song. So sánh độ dài AC và BD

A. AC > BD

B. AC < BD

C. AC = BD

D. AC = 3BD

Lời giải:

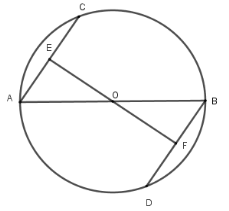
Kẻ đường thẳng qua O vuông góc với A tại E và cắt BD tại F thì EFBD tại F vì AC // BD.

Xét hai tam giác vuông OEA và tam giác OFB

có OB = OA; $\widehat{EAO}=\widehat{FBO}$ (so le trong)

Nên $\Delta AEO=\Delta BFO$ (ch-gn)

$\Rightarrow$  OE = OF $\Rightarrow$AC = DB

(hai dây cách đều tâm thì bằng nhau)

Đáp án cần chọn là:C

Câu 13: Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết AB = 10cm; CD = 8cm; MC = 1cm. Bán kinh R và khoảng cách từ tâm O đến dây CD lần lượt là:

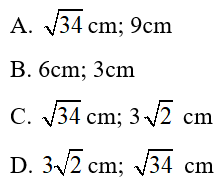
Lời giải:

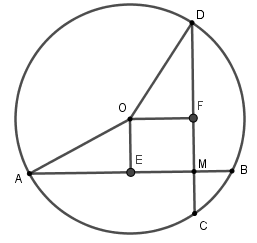
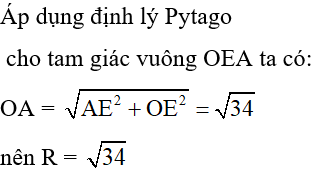
Câu 14: Cho đường tròn (O), dây cùng AB và CD với CD < AB. Giao điểm K của các đường thẳng AB và CD nằm ngoài đường tròn. Vẽ đường tròn (O; OK), đường tròn này cắt KA và KC lần lượt tại M và N. So sánh KM và KN.

A. KN > KM

B. KN < KM 

C. KM = KN

D. KN =  KM

Lời giải:

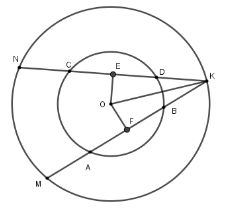
Câu 15: Cho đường tròn (O; R) có hai dây AB, CD bằng nhau và vuông góc với nhau tại I. Giả sử IA = 6cm; IB = 3cm. Tổng khoảng cách từ tâm O đến dây AB, CD là:

A. 4cm

B. 1cm 

C. 3cm

D. 2cm

Lời giải:

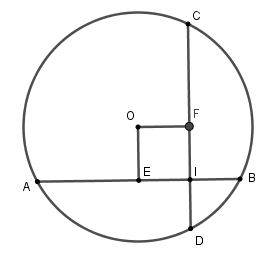
Xét đường tròn tâm (O)

Kẻ OE$\perp$AB tại E suy ra E là trung điểm của AB,

kẻ OF$\perp$CD tại F.

Vì dây AB = AC nên OE = OF

(hai dây bằng nhau cách đều tâm)

Xét tứ giác OEIF có $\widehat{E}=\widehat{F}=\widehat{I}$ = 90^o

nên OEIF là hình chữ nhật và OE = OF

nên OEIF là hình vuông$\Rightarrow$OE = OF = EI

Mà AB = IA + IB = 9cm$\Rightarrow$EB = 4,5cm  

$\Rightarrow$EI = EB – IB = 1,5cm

nên OE = OF = 1,5cm

Vậy tổng khoảng cách từ tâm đến hai dây

là AB, CD là 1,5 + 1,5 = 3cm

Đáp án cần chọn là:C

Câu 16: Cho đường tròn (O; 10cm). Dây AB và CD song song, có độ dài lần lượt là 16cm và 12cm. Tính khoảng cách giữa 2 dây.

A. 14cm

B. 10cm

C. 12cm

D. 16cm

Lời giải:

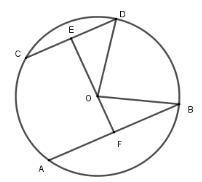
Kẻ đường thẳng qua O vuông góc với CD tại E

và cắt DB tại F thì EF  AB vì AB // CD

Khi đó E là trung điểm của CD và F là trung điểm của AB (đường kính vuông góc với dây thì đi qua trung điểm dây đó). Nên ED = 6cm; FB = 8cm; OD = OB= 10cm

Áp dụng định lý Pytago cho tam giác vuông OED ta được:

OE = $\sqrt{O{D}^2-E{D}^2}$ = 8cm

Áp dụng định lý Pytago cho tam giác vuông OFB ta được:

OF = $\sqrt{O{B}^2-F{B}^2}$ = 6cm

Vậy khoảng cách giữa hai dây là:

EF = OE + OF = 14cm

Đáp án cần chọn là:A

Câu 17: Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết CD = 8cm; MC = 1cm. Khoảng cách từ tâm O đến dây AB là?

A. 4cm 

B. 5cm

C. 3cm

D. 2cm

Lời giải:

Kẻ OE$\perp$AB tại E

suy ra E là trung điểm của AB,

kẻ OFCD tại F suy ra F là trung điểm CD

Xét tứ giác OEMF có $\widehat{E}=\widehat{F}=\widehat{M}={90}^o$

 nên OEIF là hình chữ nhật, suy ra FM = OE

Ta có CD = 8cm$\Rightarrow$FC = 4cm

mà MC = 1cm$\Rightarrow$FM = FC –MC = 4 – 1 = 3cm

nên OE = FM = 3cm

Vậy khoảng cách từ tâm O đến dây AB là 3cm

Đáp án cần chọn là:C

Câu 18: Cho đường tròn (O; R). Hai dây AB, CD song song với nhau sao cho tâm O nằm trong dải song song tạo bởi AB, CD. Biết khoảng cách giữa hai dây đó bằng 11cm và AB = 10$\sqrt{3}$cm, CD = 16cm. Tính R

A. R = 5$\sqrt{2}$ (cm)

B. R = 10$\sqrt{2}$ (cm)

C. R = 10 (cm)

D. R = 5$\sqrt{3}$ (cm)

Lời giải:

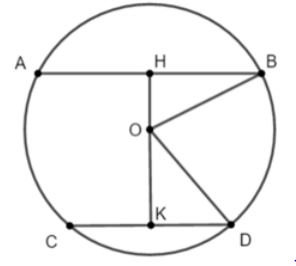
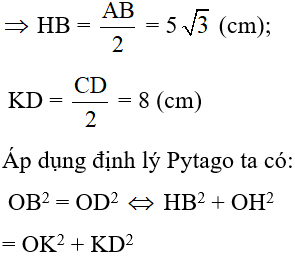
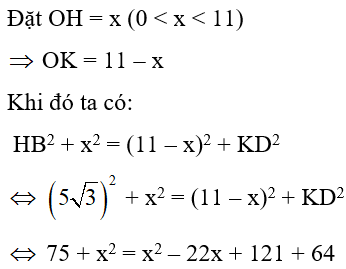
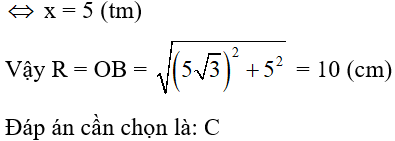
Câu 19: Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết AB = 14cm; CD = 12cm; MC = 2cm. Bán kinh R và khoảng cách từ tâm O đến dây CD lần lượt là:

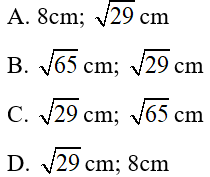
Lời giải:

Câu 20: Cho đường tròn (O) có hai dây AB, CD không đi qua tâm. Biết khoảng cách từ tâm O đến dây AB lớn hơn khoảng cách từ tâm O đến dây CD. Kết luận nào sau đây là đúng?

A. AB > CD 

B. AB = CD 

C. AB < CD

D. AB // CD

Lời giải:

Trong một đường tròn: Dây nào gần tâm hơn thì dây đó lớn hơn

Từ đề bài ta thấy dây CD gần tâm hơn dây AB nên AC > AB

Đáp án cần chọn là:C

Câu 21: Cho đường tròn (O; R = 25). Khi đó dây cung lớn nhất của đường tròn đó bằng?

A. 12,5

B. 25

C. 50

D. 20

Lời giải:

Trong đường tròn thì đường kính là dây lớn nhất của đường tròn đó. Vậy dây lớn nhất của đường tròn là 50

Đáp án cần chọn là:C

Câu 22: Cho đường tròn (O; R = 20). Cho dây cung MN có độ dài 36. Khoảng cách từ tâm O đến dây cung là?

A. 15

B. $\sqrt{35}$

C. $\sqrt{76}$

D. 20

Lời giải:

Giải thích: Khoảng cách từ O đến dây cung MN là:

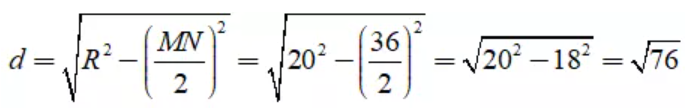
Đáp án cần chọn là:C

Câu 23: Cho đường tròn (O; R), có dây cung MN có độ dài là 24cm, khoảng cách từ O đến đường thẳng MN là 16cm. Độ dài bán kính R là?

A. 24cm

B. 25cm

C. 16cm

D. 20cm

Lời giải:

Độ dài bán kính của đường tròn là:

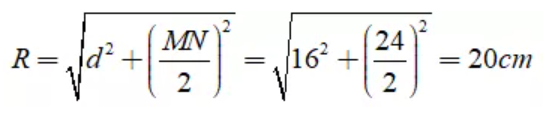
Đáp án cần chọn là:D

Câu 24: Cho đường tròn tâm O bán kính 3 cm và hai dây AB và AC. Biết AB = 5cm, AC = 2cm. Trong 2 dây AB và AC dây nào gần tâm hơn?

A. AB

B. AC

C. Chưa thể kết luận được

D. Hai dây cách đều tâm

Lời giải:

Ta có: AB > AC ( 5 cm > 2 cm) nên dây AB gần tâm hơn.

Đáp án cần chọn là:A

Câu 25: Cho đường tròn tâm O, bán kính R = 6cm ngoại tiếp tam giác ABC vuông tại A có AB = 6cm, AC = 8 cm. Trong các dây AB, BC và AC thì dây nào gần tâm hơn?

A. AB

B. BC

C. AC

D. Chưa kết luận được.

Lời giải:

Áp dụng định lí Pytago vào tam giác ABC ta có:

$B{C}^2 = A{B}^2 +A{C}^2 = 6^2+8^2 = 100$ nên BC = 100

Ta có: AB < AC < BC ( 6 cm < 8 cm < 10 cm )

Do đó, dây BC gần tâm nhất, dây AB xa tâm nhất

Tam giác ABC vuông tại A nên tâm đường tròn ngoại tiếp tam giác là trung điểm của BC

⇒ khoảng cách từ tâm đến BC là bằng 0.

Do đó, dây BC gần tâm nhất, dây AB xa tâm nhất

Đáp án cần chọn là:B

Câu 26: Cho đường tròn tâm O, bán kính R = 10cm. Tam giác ABC nội tiếp đường tròn tâm O, biết góc A là góc tù. Hỏi trong các dây AB, BC và AC thì dây nào gần tâm nhất?

A. AB

B. AC

C. BC

D. Chưa kết luận được

Lời giải:

Tam giác ABC có góc A là góc tù nên $\stackrel{⏜}{A }$> $\stackrel{⏜}{B}$; $\stackrel{⏜}{A}$>$\stackrel{⏜}{C}$

Mà cạnh đối diện với góc A là cạnh BC .

Áp dụng định lí: trong 1 tam giác cạnh đối diện với góc lớn hơn thì lớn hơn ta được:

BC > AC và BC > AB

Vậy tam giác ABC có độ dài cạnh BC là lớn nhất nên dây BC gần tâm nhất.

Đáp án cần chọn là:C

Câu 27: Cho tam giác ABC cân tại A nội tiếp đường tròn tâm (O). Tìm khẳng định đúng?

A. Hai dây AB và AC cách đều tâm.

B. Dây BC gần tâm nhất.

C. Dây BC gần tâm hơn dây AC.

D. Dây AB gần tâm hơn dây BC.

Lời giải:

Vì tam giác ABC cân tại A nên AB = AC

Suy ra: hai dây AB và AC cách đều tâm.

Đáp án cần chọn là:A

Câu 28: Cho đường tròn (O; R) có hai dây AB, CD bằng nhau và vuông góc với nhau tại I. Giả sử IA = 2cm; IB = 4cm. Tổng khoảng cách từ tâm O đến dây AB, CD là:

A. 4cm

B. 1cm

C. 3cm

D. 2cm

Lời giải:

Xét đường tròn tâm (O).

Kẻ OE
⊥
AB tại E suy ra E là trung điểm của AB,

kẻ OFCD tại F.

Vì dây AB = AC nên OE = OF

(hai dây bằng nhau cách đều tâm)

Xét tứ giác OEIF có $\stackrel{⏜}{E}$ = $\stackrel{⏜}{F}=\stackrel{⏜}{I} = 90°$

nên OEIF là hình chữ nhật và OE = OF

nên OEIF là hình vuông

⇒ OE = OF = EI

Mà AB = IA + IB = 6cm

⇒ EB = 3cm EI = EB – IB = 1cm ==>  OE = OF = 1cm

Vậy tổng khoảng cách từ tâm đến hai dây là AB, CD là 2cm

Đáp án cần chọn là:D

Câu 29: Cho đường thẳng d cắt đường tròn (O) tại hai điểm phân biệt A, B. Biết khoảng cách từ điểm O đến đường thẳng d bằng 3cm và độ dài đoạn thẳng AB bằng 8cm. Bán kính của đường tròn (O) bằng:

A. 7cm

B. 11cm

C. 73cm

D. 5cm

Lời giải:

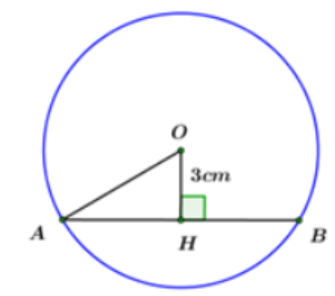
Kẻ OH ⊥ AB. Khi đó H là trung điểm của AB (mối liên hệ giữa đường kính và dây cung)

Đáp án cần chọn là:D

Câu 30: Cho đường tròn (O) có hai dây AB, CD không đi qua tâm. Biết khoảng cách từ tâm đến hai dây là bằng nhau. Kết luận nào sau đây là đúng?

A. AB > CD

B. AB = CD

C. AB < CD

D. AB // CD

Lời giải:

Đáp án: B

Đáp án cần chọn là:B

Câu 31: Cho đường tròn (O; R = 25). Khi đó dây cung lớn nhất của đường tròn đó bằng?

A. 12,5

B. 25

C. 50

D. 20

Lời giải:

Trong đường tròn thì đường kính là dây lớn nhất của đường tròn đó

Vậy dây lớn nhất của đường tròn là 50

Đáp án cần chọn là:C

Câu 32: Cho đường tròn (O), đường kính AB. Kẻ hai dây AC và BD song song. Khi đó:

A. AC = BD

B. AC = 2 BD

C. BD = 2 AC

D. Tất cả sai

Chứng minh AC = BD.

Lời giải:

Qua O dựng đường thẳng vuông góc với AC và BD. Đường thẳng này cắt AC và BD lần lượt tại M và N..

Đáp án cần chọn là:A

Câu 33: Cho đường tròn (O; 5cm). Dây AB và CD song song, có độ dài lần lượt là 8 cm và 6 cm. Tính khoảng cách giữa hai dây.

A. 6 cm

B.8 cm

C. 7 cm

D. 9 cm

Lời giải:

Qua O dựng đường thẳng vuông góc với AB và CD, cắt AB và CD lần lượt tại M và N.

Ta có:

Áp dụng định lí Py tago vào tam giác vuông OND và OMB ta có:

Khoảng cách hai dây AB và CD là: MN = OM + ON = 3 + 4 = 7 cm

Đáp án cần chọn là:C

Câu 34: Cho đường tròn (O) đường kính AB = 13 cm, dây CD có độ dài 12 cm vuông góc với AB tại H ( H nằm giữa O và A). Tính HB.

A. 6cm

B. 8cm

C. 9cm

D. 10 cm

Lời giải:

Do AB là đường kính nên bán kính đường tròn là:

Đáp án cần chọn là:B

Câu 35: Cho đường tròn tâm O bán kính 3 cm và hai dây AB và AC. Biết AB = 5cm, AC = 2cm. Trong 2 dây AB và AC dây nào gần tâm hơn?

A. AB

B. AC

C. Chưa thể kết luận được

D. Hai dây cách đều tâm

Lời giải:

Ta có: AB > AC ( 5 cm > 3 cm) nên dây AB gần tâm hơn.

Đáp án cần chọn là:A

Câu 36: Cho đường tròn tâm O, bán kính R = 6cm ngoại tiếp tam giác ABC vuông tại A có AB = 6cm, AC = 8 cm. Trong các dây AB , BC và AC thì dây nào gần tâm hơn?

A. AB

B. BC

C. AC

D. chưa kết luận được.

Lời giải:

Áp dụng định lí Pytago vào tam giác ABC ta có:

BC² = AB² + AC² = 6² + 8² = 100 nên BC =10 cm

Ta có: AB < AC < BC ( 6 cm < 8 cm < 10 cm )

Do đó, dây BC gần tâm nhất, dây AB xa tâm nhất

Đáp án cần chọn là:B

Câu 37: Cho đường tròn tâm O, bán kính R = 10cm. Tam giác ABC nội tiếp đường tròn tâm O, biết góc A là góc tù. Hỏi trong các dây AB, BC và AC thì dây nào gần tâm nhất?

A. AB

B. AC

C. BC

D. Chưa kết luận được

Lời giải:

Tam giác ABC có góc A là góc tù nên 

Mà cạnh đối diện với góc A là cạnh BC .

Áp dụng định lí: trong 1 tam giác cạnh đối diện với góc lớn hơn thì lớn hơn ta được:

BC > AC và BC > AB

Vậy tam giác ABC có độ dài cạnh BC là lớn nhất nên dây BC gần tâm nhất.

Chưa thể kết luận dây nào xa tâm nhất.

Đáp án cần chọn là:C

Câu 38: Cho tam giác ABC cân tại A nội tiếp đường tròn tâm (O). Tìm khẳng định đúng?

A. Hai dây AB và AC cách đều tâm.

B. Dây BC gần tâm nhất.

C. Dây BC gần tâm hơn dây AC.

D. Dây AB gần tâm hơn dây BC.

Lời giải:

Vì tam giác ABC cân tại A nên AB = AC

Suy ra: hai dây AB và AC cách đều tâm.

Ta chưa thể so sánh độ dài AB và BC; AC và BC nên ta chưa thể kết luận dây nào gần tâm hơn, dây nào xa tâm hơn hay các dây cách đều tâm.

Đáp án cần chọn là:A

Câu 39: Cho đường tròn (O; R = 20). Cho dây cung MN có độ dài 36. Khoảng cách từ tâm O đến dây cung là?

A. 15

B. √35

C. √76

D. 20

Lời giải:

Khoảng cách từ O đến dây cung MN là:

Đáp án cần chọn là:C

Câu 40: Cho đường tròn (O; R), có dây cung MN có độ dài là 24cm, khoảng cách từ O đến đường thẳng MN là 16cm. Độ dài bán kính R là?

A. 24cm

B. 25cm

C. 16cm

D. 20cm

Lời giải:

Độ dài bán kính của đường tròn là:

Đáp án cần chọn là:D