Toptailieu.vn giới thiệu Giải bài tập Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Căn bậc hai lớp 9.
Giải bài tập Toán 9 Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây
Trả lời câu hỏi giữa bài:
Trả lời câu hỏi 1 trang 105 SGK Toán 9 Tập 1: Hãy sử dụng kết quả của bài toán ở mục 1 để chứng minh rằng:
a) Nếu AB = CD thì OH = OK.
b) Nếu OH = OK thì AB = CD.
Lời giải:
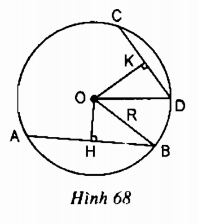
Xét đường tròn có
OH là một phần đường kính vuông góc với dây AB
H là trung điểm của (Định lí)
OK là một phần đường kính vuông góc với dây CD
K là trung điểm của (Định lí)
Theo mục 1:
a) Nếu
mà
b) Nếu
mà
Trả lời câu hỏi 2 trang 105 SGK Toán 9 Tập 1: Hãy sử dụng kết quả bài toán ở mục 1 để so sánh các độ dài:
a) OH và OK, nếu biết AB>CD
b) AB và CD, nếu biết OH<OK
Lời giải:
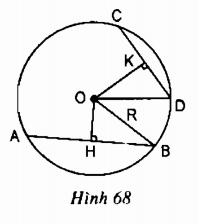
Xét đường tròn có
OH là một phần đường kính vuông góc với dây AB
H là trung điểm của (Định lí)
OK là một phần đường kính vuông góc với dây CD
K là trung điểm của (Định lí)
Theo mục 1:
a) Nếu
mà
b) Nếu
mà
Trả lời câu hỏi 3 trang 105 SGK Toán 9 Tập 1: Cho tam giác ABC, O là giao của các đường trung trực của tam giác; D, E, F theo thứ tự là trung điểm của các cạnh Cho biết (h.69).
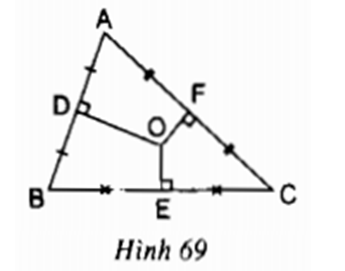
Hãy so sánh các độ dài:
a) BC và AC;
b) AB và AC.
Phương pháp giải:
Sử dụng:
Trong hai dây của một đường tròn:
+ Hai dây cách đều tâm thì bằng nhau
+ Dây nào xa tâm hơn thì dây đó nhỏ hơn
Lời giải:
Vì O là giao điểm của 3 đường trung trực của tam giác ABC
⇒ O là tâm đường tròn ngoại tiếp tam giác ABC
a) Vì suy ra (hai dây cách đều tâm thì bằng nhau)
b) Vì nên (dây nào gần tâm hơn thì dây đó lớn hơn) mà (câu a) nên
Bài tập trang 106 SGK Toán 9
Bài 12 trang 106 SGK Toán 9 - tập 1: Cho đường tròn tâm bán kính , dây bằng .
a) Tính khoảng cách từ tâm đến dây .
b) Gọi là điểm thuộc dây sao cho . Kẻ dây đi qua và vuông góc với . Chứng minh rằng
Phương pháp giải:
a) +) Sử dụng định lý: Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Sử dụng định lí Pytago: , vuông tại thì .
b) Sử dụng định lý: Trong một đường tròn, hai dây cách đều nhau thì bằng nhau.
Lời giải:
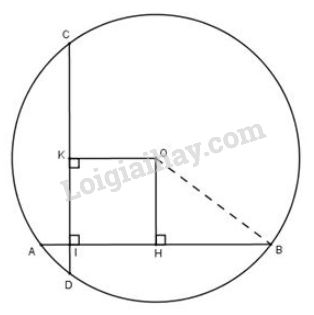
a) Kẻ tại H
Khi đó, đường tròn (O) có OH là 1 phần đường kính vuông góc với dây AB tại H
Suy ra là trung điểm của dây (Theo định lí 2 - trang 103)
Xét tam giác vuông tại , theo định lí Pytago, ta có:
.
Vậy khoảng cách từ tâm đến dây là .
b) Vẽ tại K
Tứ giác có ba góc vuông nên là hình chữ nhật, suy ra .
Ta có , suy ra
Vậy
Hai dây và cách đều tâm nên chúng bằng nhau.
Do đó
Bài 13 trang 106 sgk Toán 9 - tập 1: Cho đường tròn có các dây và bằng nhau, các tia và cắt nhau tại điểm nằm bên ngoài đường tròn. Gọi và theo thứ tự là trung điểm của và . Chứng minh rằng:
a)
b) .
Phương pháp giải:
a) Sử dụng các tính chất sau: Trong một đường tròn
+) Đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
+) Hai dây bằng nhau thì cách đều tâm.
b) Cộng đoạn thẳng
Lời giải:
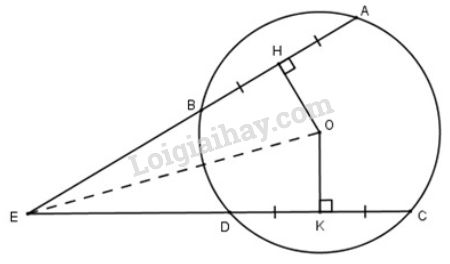
a) Nối OE.
Vì nên (đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)
Vì nên . (đường kính đi qua trung điểm của dây không đi qua tâm thì vuông góc với dây đó)
Mà nên (hai dây bằng nhau thì cách đều tâm).
Xét và có:
chung
(cạnh huyền - cạnh góc vuông)
( 2 cạnh tương ứng)
b) Vì nên hay (2)
Từ (1) và (2)
hay
Bài 14 trang 106 SGK Toán 9 tập 1: Cho đường tròn tâm bán kính , dây bằng . Vẽ dây song song với và có khoảng cách đến bằng . Tính độ dài dây .
Phương pháp giải:
+) Kẻ đường kính vuông góc với dây.
+) Sử dụng định lý: Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây ấy.
+) Sử dụng định lí Pytago: vuông tại thì .
Lời giải:
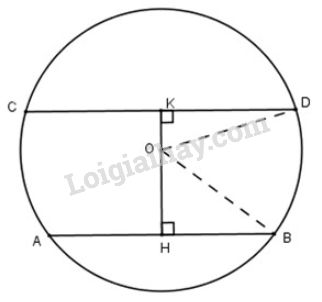
Vẽ , đường thẳng cắt tại .
Vì mà suy ra hay .
Ta có và nên và (vì đường kính vuông góc với dây thì đi qua trung điểm của dây ấy)
Ta có: .
Áp dụng định lí Pytago vào tam giác vuông tại , ta có:
Lại có:
Áp dụng định lí Pytago vào tam giác vuông tại , ta có:
Bài 15 trang 106 sgk Toán 9 - tập 1: Cho hình trong đó hai đường tròn cùng có tâm là . Cho biết .
Hãy so sánh các độ dài:
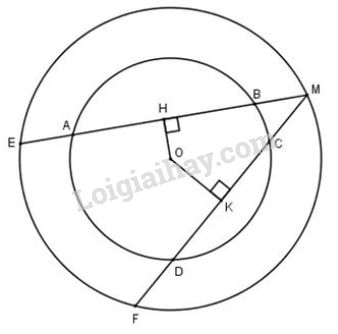
a) và ;
b) và ;
c) và .
Phương pháp giải:
+) Để so sánh hai dây, ta đi so sánh khoảng cách từ tâm đến hai dây ấy và ngược lại.
+) Sử dụng tính chất: Trong một đường tròn:
a) Dây nào lớn hơn thì dây đó gần tâm hơn.
b) Dây nào gần tâm hơn thì dây đó lớn hơn.
c) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
Lời giải:
a) Xét trong đường tròn nhỏ:
Theo định lí : trong hai dây của một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn.
Theo giả thiết suy ra gần tâm hơn, tức là .
b) Xét trong đường tròn lớn:
Theo định lí : trong hai dây của một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.
Theo câu , ta có: .
c) Xét trong đường tròn lớn:
Vì (Định lý 2 - trang 103).
Vì (Định lý 2 - trang 103).
Theo câu , ta có:
Bài 16 trang 106 sgk Toán 9 - tập 1: Cho đường tròn , điểm nằm bên trong đường tròn. Vẽ dây vuông góc với tại . Vẽ dây bất kì đi qua và không vuông góc với . Hãy so sánh độ dài hai dây và .
Phương pháp giải:
- Để so sánh hai dây, ta đi so sánh khoảng cách từ tâm đến hai dây đó.
- Sử dụng các tính chất sau:
+) Trong tam giác vuông, cạnh huyền là cạnh lớn nhất.
+) Trong một đường tròn, dây nào gần tâm hơn thì dây đó lớn hơn.
Lời giải:
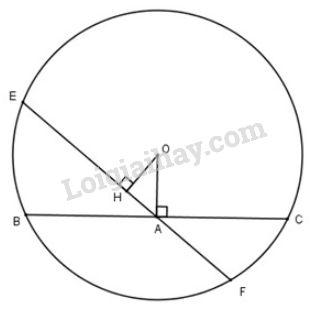
Vẽ tại H.
Xét tam giác vuông tại có là cạnh huyền
Do đó (trong tam giác vuông, cạnh huyền là cạnh lớn nhất)
(dây nào gần tâm hơn thì dây đó lớn hơn).
Nhận xét. Trong các dây đi qua một điểm ở trong đường tròn, dây vuông góc với là dây ngắn nhất.
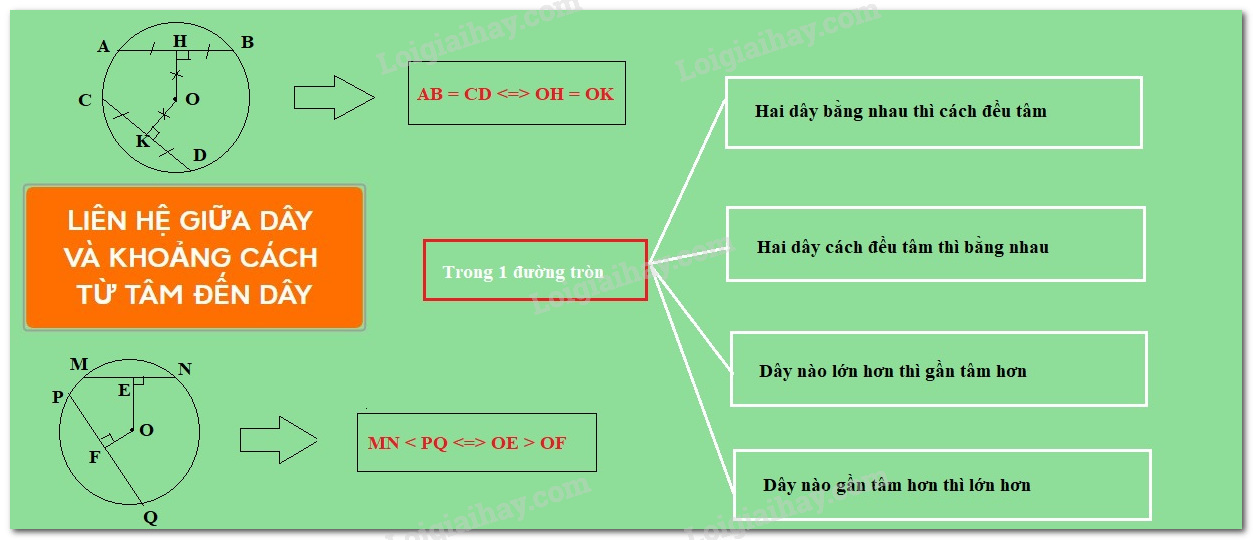
Lý thuyết Bài 3: Liên hệ giữa dây và khoảng cách từ tâm đến dây
1. Liên hệ giữa dây và khoảng cách từ tâm đến dây
Định lý 1: Trong một đường tròn:
a) Hai dây bằng nhau thì cách đều tâm.
b) Hai dây cách đều tâm thì bằng nhau.
Định lý 2. Trong hai dây của một đường tròn:
a) Dây nào lớn hơn thì dây đó gần tâm hơn.
b) Dây nào gần tâm hơn thì dây đó lớn hơn.
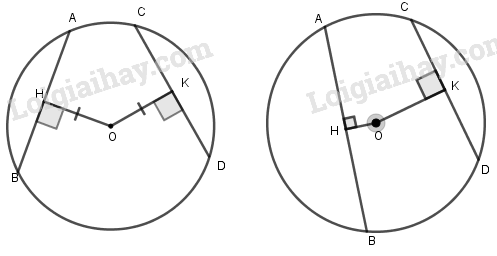
Xét đường tròn (O):
Khi đó:
2. CÁC DẠNG TOÁN THƯỜNG GẶP
So sánh hai đoạn thẳng
Phương pháp:
Ta thường sử dụng các kiến thức sau:
- Trong một đường tròn:
+ Hai dây bằng nhau thì cách đều tâm.
+ Hai dây cách đều tâm thì bằng nhau.
- Trong hai dây của một đường tròn:
+ Dây nào lớn hơn thì dây đó gần tâm hơn.
+ Dây nào gần tâm hơn thì dây đó lớn hơn,
- Chứng minh hai tam giác bằng nhau, quan hệ giữa các yếu tố trong tam giác.