Toptailieu.vn giới thiệu Giải bài tập Toán 9 Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Căn bậc hai lớp 9.
Giải bài tập Toán 9 Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn
Trả lời câu hỏi giữa bài:
Trả lời câu hỏi 1 trang 110 SGK Toán 9 Tập 1: Cho tam giác ABC, đường cao AH. Chứng minh rằng đường thẳng BC là tiếp tuyến của đường tròn (A; AH).
Phương pháp giải:
Sử dụng: Đường thẳng đi qua một điểm thuộc đường tròn và vuông góc với bán kính đi qua điểm đó là tiếp tuyến của đường tròn.
Lời giải:
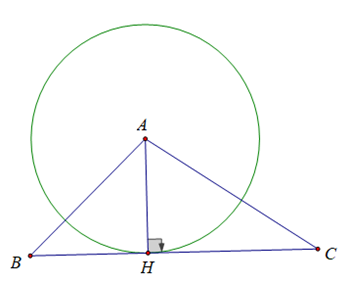
Ta có: BC đi qua điểm H thuộc đường tròn (A; AH)
tại H
BC là tiếp tuyến của đường tròn (A; AH)
Trả lời câu hỏi 2 trang 111 SGK Toán 9 Tập 1: Hãy chứng minh cách dựng trên là đúng.
Phương pháp giải:
Sử dụng: Đường thẳng đi qua một điểm thuộc đường tròn và vuông góc với bán kính đi qua điểm đó là tiếp tuyến của đường tròn.
Lời giải:
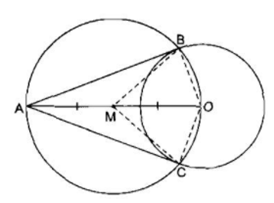
Ta có: MA = MO = MB ( cùng bằng bán kính đường tròn tâm M, bán kính MO)
cân tại
cân tại
Mặt khác ta lại có: (tổng 3 góc trong tam giác)
Từ (1) và (2)
Suy ra tại , mà
Do đó AB là tiếp tuyến của (O)
Chứng minh tương tự,
Ta có: MA = MO = MC ( cùng bằng bán kính đường tròn tâm M, bán kính MO)
cân tại
cân tại
Mặt khác ta lại có: (tổng 3 góc trong tam giác)
Từ (3) và (4)
Suy ra tại , mà
Do đó AC là tiếp tuyến của (O)
Bài tập trang 111 SGK Toán 9
Bài 21 trang 111 sgk Toán 9 - tập 1: Cho tam giác có . Vẽ đường tròn . Chứng minh rằng là tiếp tuyến của đường tròn.
Phương pháp giải:
+) Định lí Pytago đảo: Tam giác có thì là tam giác vuông tại .
+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Lời giải:
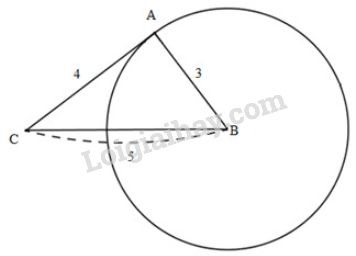
Xét tam giác ta có:
(vì
Theo định lý Pytago đảo, ta có tam giác vuông tại
tại .
Xét đường tròn (B;BA) có đường thẳng AC đi qua điểm A thuộc đường tròn và AC vuông góc với bán kính BA nên là tiếp tuyến của đường tròn.
Bài 22 trang 111 sgk Toán 9 - tập 1: Cho đường thẳng , điểm nằm trên đường thẳng , điểm nằm ngoài đường thẳng . Hãy dựng đường tròn đi qua điểm và tiếp xúc với đường thẳng tại .
Phương pháp giải:
+) Bài toán dựng hình chia làm bước:
Bước 1. Phân tích: giả sử hình cần dựng đã được vẽ. Lập luận để tìm cách dựng được hình.
Bước 2. Dựng hình: Dựa vào bước phân tích trên liệt kê thứ tự các phép dựng hình cơ bản.
Bước 3. Chứng minh: Bằng lí luận, chứng minh hình vừa dựng thỏa mãn tất cả các giả thiết của bài toán.
Bước 4. Biện luận: thiết lập điều kiện giải được của bài toán. Tức là xét xem bài toán giải được trong trường hợp nào và có bao nhiêu nghiệm.
+) Sử dụng các tính chất: Mọi điểm nằm trên đường trung trực của đoạn thì cách đều hai điểm
Lời giải:
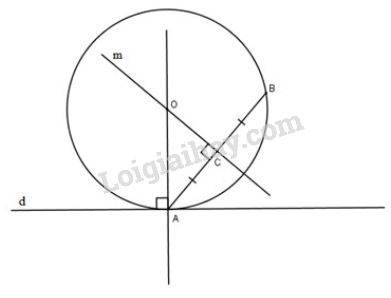
Phân tích:
Giả sử đã dựng được đường tròn thỏa mãn đề bài.
Tâm thỏa mãn hai điều kiện:
- nằm trên đường trung trực của (vì đường tròn đi qua và ).
- nằm trên đường thẳng vuông góc với tại (vì đường tròn tiếp xúc với đường thẳng tại ).
Vậy là giao điểm của hai đường thẳng nói trên.
Cách dựng:
- Dựng đường trung trực của .
- Từ dựng một đường thẳng vuông góc với cắt đường thẳng tại .
- Dựng đường tròn . Đó là đường tròn phải dựng.
Chứng minh:
Vì nằm trên đường trung trực của nên , do đó đường tròn đi qua và .
Đường thẳng tại nên đường thẳng tiếp xúc với đường tròn tại .
Biện luận: Bài toán luôn có nghiệm hình.
Bài 23 trang 111 sgk Toán 9 - tập 1: Dây cua-roa trên hình 76 có những phần là tiếp tuyến của các đường tròn tâm. Chiều quay của đường tròn tâm ngược chiều quay của kim đồng hồ. Tìm chiều quay của đường tròn tâm và đường tròn tâm (cùng chiều quay hay ngược chiều quay của kim đồng hồ).
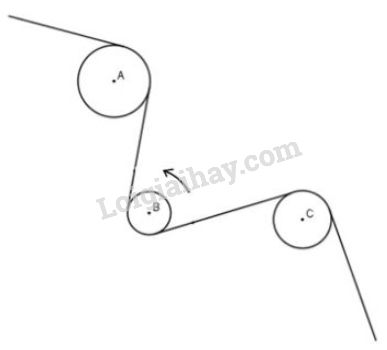
Phương pháp giải:
Nếu dây cua-roa mắc qua hai đường tròn mà cắt đoạn thẳng nối hai tâm đường tròn thì chiều quay của hai đường tròn sẽ ngược nhau.
Lời giải:
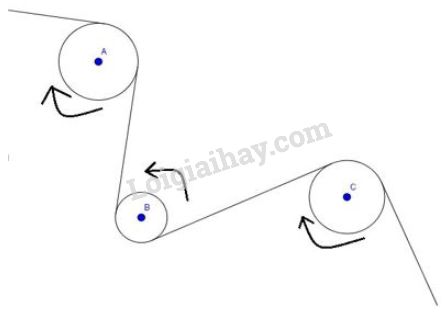
Ta thấy đường tròn tâm và đường tròn tâm cùng nằm phía dưới dây cua-roa nên sẽ quay cùng chiều nhau.
Đường tròn tâm nằm phía trên dây cua-roa nên quay ngược chiều so với hai đường tròn tâm và tâm .
Mà đường tròn tâm quay ngược chiều kim đồng hồ nên đường tròn tâm và tâm quay cùng chiều kim đồng hồ.
Bài 24 trang 111 SGK Toán 9 tập 1: Cho đường tròn , dây khác đường kính. Qua kẻ đường vuông góc với , cắt tiếp tuyến tại của đường tròn ở điểm .
a) Chứng minh rằng là tiếp tuyến của đường tròn.
b) Cho bán kính của đường tròn bằng . Tính độ dài .
Phương pháp giải:
a) Dùng dấu hiệu nhận biết tiếp tuyến: Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Sử dụng tính chất:
+) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Nếu một đường thẳng là tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm đó.
b) Sử dụng định lí Pytago: vuông tại , khi đó: .
Sử dụng hệ thức lượng trong tam giác vuông: , vuông tại , , khi đó: .
Lời giải:
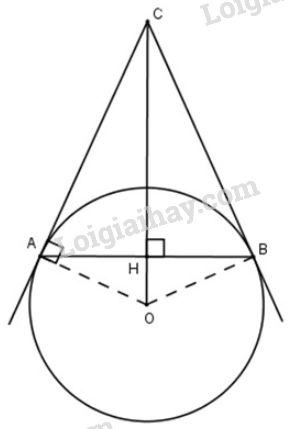
a) Gọi là giao điểm của và .
Xét đường tròn (O) có tại H mà OH là 1 phần đường kính và AB là dây của đường tròn nên (Định lý 2 - trang 103).
Suy ra là đường trung trực của , do đó (tính chất)
Xét và có:
chung
(chứng minh trên)
Suy ra (c.c.c)
( 2 góc tương ứng) (1)
Vì là tiếp tuyến của đường tròn nên:
(2)
Từ (1) và (2) suy ra .
Tức là vuông góc với , mà là bán kính của .
Vậy là tiếp tuyến của đường tròn .
b) Ta có:
.
Xét tam giác vuông tại , áp dụng định lí Pytago, ta có:
Xét tam giác vuông tại , áp dụng hệ thức lượng trong tam giác vuông, ta có:
Bài 25 trang 111 sgk Toán 9 - tập 1: Cho đường tròn tâm có bán kính , dây vuông góc với tại trung điểm của .
a) Từ giác là hình gì? Vì sao?
b) Kẻ tiếp tuyến với đường tròn tại , nó cắt đường thẳng tại . Tính độ dài theo .
Phương pháp giải:
a) +) Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.
+) Hình bình hành có hai đường chéo vuông góc là hình thoi.
b) Hệ thức lượng giữa cạnh và góc trong tam giác vuông: vuông tại , đường cao thì
Lời giải:
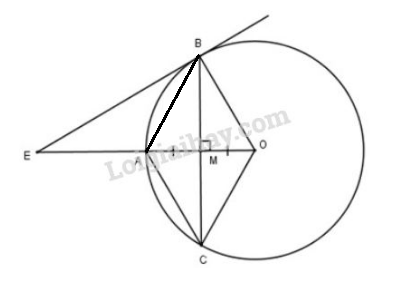
a) Xét đường tròn (O) có OA là 1 phần đường kính và BC là dây của đường tròn mà (Theo định lý 2 - trang 103).
Lại có (vì là trung điểm)
Tứ giác là hình bình hành (vì có các đường chéo OA và BC cắt nhau tại trung điểm M mỗi đường)
Mặt khác,
Do đó là hình thoi (hình bình hành có hai đường chéo vuông góc nên là hình thoi).
b) Ta có là hình thoi nên (tính chất)
Mà
. Do đó tam giác đều (Dấu hiệu nhận biết)
(Tính chất)
Ta có là tiếp tuyến của tại hay .
Xét tam giác vuông tại , áp dụng hệ thức giữa cạnh và góc trong tam giác vuông, ta có:
Lý thuyết Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn
1. Các kiến thức cần nhớ
a) Tính chất của tiếp tuyến
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
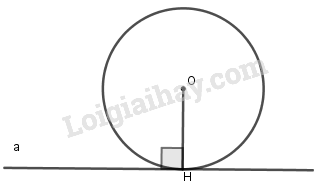
Trong hình trên a là tiếp tuyến của đường tròn
tại (với H là tiếp điểm).
b) Dấu hiệu nhận biết tiếp tuyến của đường tròn
Định lý: Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.
Ngoài ra, nhắc lại một số dấu hiệu đã biết:
+) Nếu một đường thằng và một đường tròn chỉ có một điểm chung thì đường thẳng đó là tiếp tuyến của đường tròn.
+) Nếu khoảng cách từ tâm của một đường tròn đến đường thẳng bằng bán kính của đường tròn thì đường thẳng đó là tiếp tuyến của đường tròn.
2. Các dạng toán thường gặp
Dạng 1: Chứng minh một đường thẳng là tiếp tuyến của đường tròn
Phương pháp:
Để chứng minh đường thẳng là tiếp tuyến của đường tròn tại tiếp điểm là , ta có thể làm theo cách sau:
Cách 1. Chứng minh tại và .
Cách 2. Vẽ . Chứng minh .
Cách 3. Vẽ tiếp tuyến của . Ta chứng minh .
Dạng 2: Bài toán tính độ dài
Phương pháp:
Vận dụng định lý về tiếp tuyến và hệ thức lượng trong tam giác vuông để tính toán.

