Toptailieu.vn giới thiệu Giải bài tập Toán 9 Bài 3: Góc nội tiếp chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Căn bậc hai lớp 9.
Giải bài tập Toán 9 Bài 3: Góc nội tiếp
Trả lời câu hỏi giữa bài:
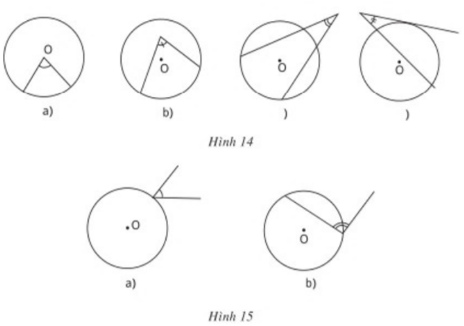
Trả lời câu hỏi 1 trang 73 SGK Toán 9 Tập 2: Vì sao các góc ở hình 14 và hình 15 không phải là góc nội tiếp ?
Phương pháp giải:
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
Lời giải:
Các góc trên hình 14 không phải góc nội tiếp vì các góc này không có đỉnh nằm trên đường tròn
Các góc trên hình 15 không phải góc nội tiếp vì các góc này không có hai cạnh chứa hai dây cung của đường tròn.
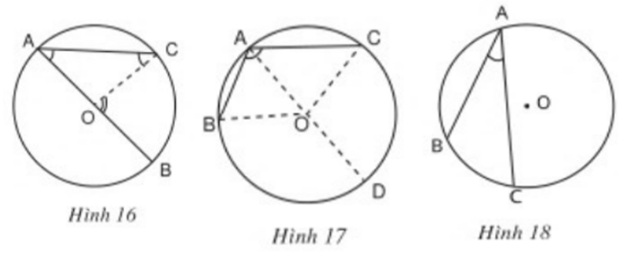
Trả lời câu hỏi 2 trang 73 SGK toán 9 Tập 2: Bằng dụng cụ, hãy so sánh số đo của góc nội tiếp ∠(BAC) với số đo của cung bị chắn BC trong mỗi hình 16, 17, 18 dưới đây.
Phương pháp giải:
Sử dụng thước đo độ để đo các góc
Lời giải:
Sử dụng thước đo độ để đo các góc, ta đo các góc BAC và BOC từ đó ta rút ra kết luận:
Trả lời câu hỏi 3 trang 75 SGK Toán 9 Tập 2: Hãy vẽ hình minh họa các tính chất trên.
Lời giải:
a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau
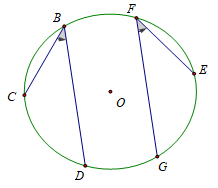
b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau
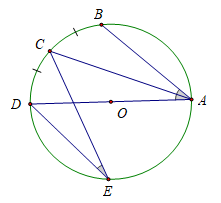
c) Góc nội tiếp (nhỏ hơn hoặc bằng 90o) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung
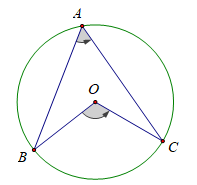
d) Góc nội tiếp chắn nửa đường tròn là góc vuông
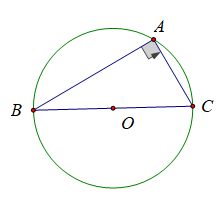
Bài tập trang 75-76 SGK Toán 9
Bài 15 trang 75 sgk Toán lớp 9 tập 2: Các khẳng định sau đúng hay sai?
a) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.
b) Trong một đường tròn, các góc nội tiếp bằng nhau thì cùng chắn một cung.
Phương pháp giải:
Hệ quả:
Trong một đường tròn:
a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
c) Góc nội tiếp (nhỏ hơn hoặc bằng ) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
d) Góc nội tiếp chắn nửa đường tròn là góc vuông.
Lời giải:
a) Đúng (Theo hệ quả: Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau)
b) Sai, vì trong một đường tròn các góc nội tiếp bằng nhau có thể là chắn các cung bằng nhau hoặc cùng chắn một cung.
Bài 16 trang 75 sgk Toán lớp 9 tập 2: Xem hình 19 ( hai đường tròn có tâm là B, C và điểm B nằm trên đường tròn tâm C).
a) Biết = , tính .
b) Nếu = thì có số đo là bao nhiêu?

Phương pháp giải:
Góc nội tiếp (nhỏ hơn hoặc bằng ) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Lời giải:
a) Xét đường tròn tâm có: là góc nội tiếp chắn cung ; là góc ở tâm chắn cung nên
Lại xét đường tròn tâm có là góc nội tiếp chắn cung ; là góc ở tâm chắn cung nên
b) Theo a) ta có
Nếu thì
Bài 17 trang 75 sgk Toán lớp 9 tập 2: Muốn xác định tâm của một đường tròn mà chỉ dùng êke thì phải làm như thế nào?
Phương pháp giải:
Sử dụng:
+ Các góc nội tiếp chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
+ Góc nội tiếp chắn nửa đường tròn là góc vuông
Lời giải:
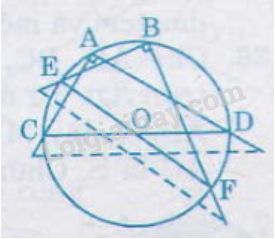
Vận dụng hệ quả: Góc nội tiếp chắn nửa đường tròn là góc vuông
+ Đặt đỉnh vuông của ê ke trùng với 1 điểm B bất kì trên đường tròn. Vẽ 2 dây cung BE, BF. Ta được tam giác BEF nội tiếp đường tròn đường kính EF
+ Đặt đỉnh vuông của ê ke trùng với 1 điểm A bất kì trên đường tròn. Vẽ 2 dây cung AC, AD. Ta được tam giác ACD nội tiếp đường tròn đường kính CD
+ Tâm đường tròn chính là giao điểm O của hai cạnh huyền DC và EF của hai tam giác vuông nội tiếp đường tròn.
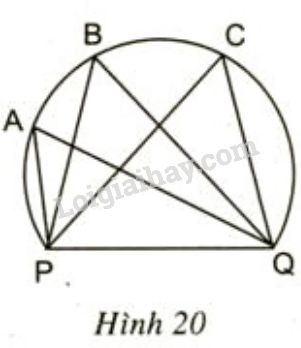
Bài 18 trang 75 sgk Toán lớp 9 tập 2: Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn . Bóng được đặt ở các vị trí trên một cung tròn như hình 20.
Hãy so sánh các góc , , .
Phương pháp giải:
Trong một đường tròn:
Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Lời giải:
Với các vị trí trên một cung tròn thì ta được các góc nội tiếp ,, cùng chắn một cung , nên suy ra = = .
Vậy với các vị trí trên thì các góc sút đều bằng nhau, không có góc sút nào rộng hơn.
Bài 19 trang 75 sgk Toán lớp 9 tập 2: Cho một đường tròn tâm , đường kính và là một điểm nằm ngoài đường tròn. và lần lượt cắt đường tròn tại . Gọi là giao điểm của và . Chứng minh rằng vuông góc với .
Phương pháp giải:
Sử dụng góc nội tiếp chắn nửa đường tròn là góc vuông để chỉ ra các đường cao của tam giác
Sử dụng tính chất trực tâm để suy ra
Lời giải:

Xét đường tròn tâm có là đường kính nên ( góc nội tiếp chắn nửa đường tròn)
Suy ra mà tại nên là trực tâm tam giác
Do đó (vì trong một tam giác ba đường cao đồng quy)
Bài 20 trang 76 sgk Toán lớp 9 tập 2: Cho hai đường tròn và cắt nhau tại và . Vẽ các đường kính và của hai đường tròn. Chứng minh rằng ba điểm thẳng hàng.
Phương pháp giải:
Sử dụng góc nội tiếp chắn nửa đường tròn là góc vuông.
Từ đó chứng minh
Lời giải:
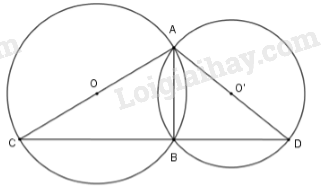
Nối với 3 điểm .
Xét đường tròn có là góc nội tiếp chắn nửa đường tròn nên
Xét đường tròn có là góc nội tiếp chắn nửa đường tròn nên
Suy ra nên thẳng hàng.
Bài 21 trang 76 sgk Toán lớp 9 tập 2: Cho hai đường tròn bằng nhau và cắt nhau tại và . Vẽ đường thẳng qua cắt tại và cắt tại ( nằm giữa và ). Hỏi là tam giác gi? Tại sao?
Phương pháp giải:
Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Lời giải:
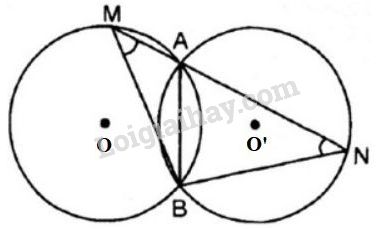
Vì hai đường tròn và bằng nhau nên cung của và bằng nhau
Suy ra (các góc nội tiếp chắn các cung bằng nhau thì bằng nhau)
Do đó tam giác là tam giác cân tại
Bài 22 trang 76 sgk Toán lớp 9 tập 2: Trên đường tròn đường kính , lấy điểm (khác và ). Vẽ tiếp tuyến của (O) tại . Đường thẳng cắt tiếp tuyến đó tại . Chứng minh rằng ta luôn có:
Phương pháp giải:
+ Sử dụng góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Sử dụng hệ thức lượng trong tam giác vuông
+ Hoặc ta chứng minh đồng dạng với từ đó suy ra tỉ lệ cạnh để có đẳng thức cần chứng minh.
Lời giải:
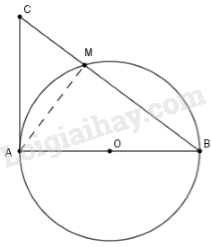
Xét có (góc nội tiếp chắn nửa đường tròn) suy ra
Lại có là tiếp tuyến tại A nên
Xét tam giác ABC vuông tại A có AM là đường cao, theo hệ thức lượng trong tam giác vuông ta có:
(đpcm)
Cách khác:
+ Xét có (góc nội tiếp chắn nửa đường tròn) suy ra .
Lại có là tiếp tuyến nên
+ Ta có (vì tam giác vuông tại ) và (do ) nên
+ Xét và có chung và (cmt) nên đồng dạng với suy ra (đpcm)
Bài 23 trang 76 sgk Toán lớp 9 tập 2: Cho đường tròn và một điểm cố định không nằm trên đường tròn. Qua kẻ hai đường thẳng. Đường thẳng thứ nhất cắt tại và .Đường thẳng thứ nhất cắt tại và .
Chứng minh
Phương pháp giải:
Sử dụng tam giác đồng dạng để suy ra hệ thức cần chứng minh
Lời giải:
Xét hai trường hợp:
a) ở bên trong đường tròn (hình a)
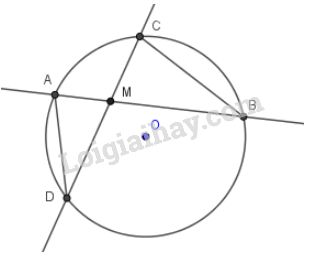
Xét hai tam giác và có:
= ( đối đỉnh)
= (hai góc nội tiếp cùng chắn cung ).
Do đó đồng dạng (g-g), suy ra:
( 2 cặp cạnh tương ứng tỉ lệ).
Do đó
b) M ở bên ngoài đường tròn (hình b)
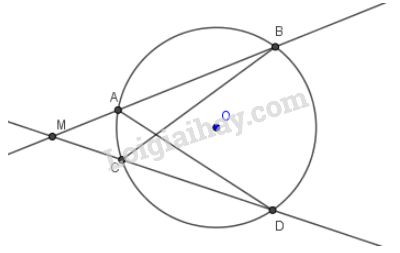
Tương tự, xét hai tam giác và có:
chung
= (hai góc nội tiếp cùng chắn cung ).
Nên đồng dạng (g-g)
Suy ra: ( 2 cặp cạnh tương ứng tỉ lệ).
Do đó:
Bài 24 trang 76 sgk Toán lớp 9 tập 2: Một chiếc cầu được thiết kế như hình 21 có độ dài m, chiều cao m. Hãy tính bán kính của đường tròn chứa cung
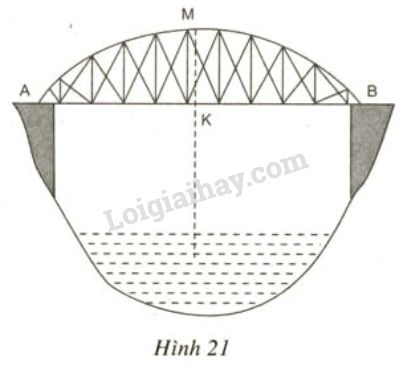
Lời giải:
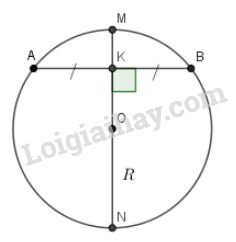
Gọi là đường kính của đường tròn có cung tròn là
Theo kết quả của bài tập 23, ta có:
hay
Ta có:
Thay số, ta có:
do đó .
Vậy = (mét)
Bài 25 trang 76 sgk Toán lớp 9 tập 2: Dựng một tam giác vuông, biết cạnh huyền dài cm và một cạnh góc vuông dài cm
Phương pháp giải:
Sử dụng hệ quả: "Góc nội tiếp chắn nửa đường tròn là góc vuông" để vẽ tam giác vuông thỏa mãn điều kiện đề bài.
Lời giải:
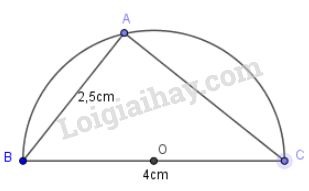
Cách vẽ như sau:
- Vẽ đoạn thẳng dài .
- Vẽ nửa đưởng tròn đường kính .
- Vẽ dây dài .
Ta có tam giác thỏa mãn các yêu cầu của đầu bài.
( =, )
Bài 26 trang 76 sgk Toán lớp 9 tập 2: Cho là ba dây của đường tròn . Từ điểm chính giữa của vẽ dây song song với dây . Gọi giao điểm của và là . Chứng minh và
Phương pháp giải:
Ta sử dụng các kiến thức sau:
+ Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
+ Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Từ đó chỉ ra các góc bằng nhau để có tam giác cân, suy ra các cặp cạnh bằng nhau.
Lời giải:
Ta có:
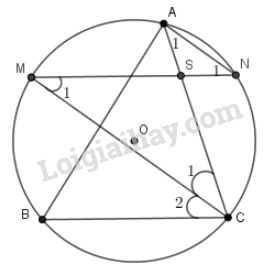
Vì M là điểm nằm chính giữa của nên
+) Chứng minh SM = SC
Vì MN // BC nên (2 góc so le trong)
Trong đường tròn (O): (2 góc nội tiếp chắn 2 cung bằng nhau )
Nên suy ra
Suy ra tam giác SMC là tam giác cân tại S. Vậy
+) Chứng minh SA = SN
Trong đường tròn (O):
( 2 góc nội tiếp cùng chắn cung NC)(1)
(2 góc nội tiếp cùng chắn cung AM)(2)
Mà (chứng minh trên)(3)
Từ (1),(2) và (3)
Vậy tam giác SAN cân tại S. Nên (đpcm)
Lý thuyết Bài 3: Góc nội tiếp
1. Các kiến thức cần nhớ
Định nghĩa góc nội tiếp
- Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
- Cung nằm bên trong góc nội tiếp được gọi là cung bị chắn.
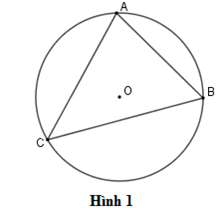
Ví dụ: Trên hình , góc là góc nội tiếp chắn cung
Định lý
Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
Ví dụ: Trên hình , số đo góc bằng nửa số đo cung nhỏ .
Hệ quả
Trong một đường tròn:
a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
c) Góc nội tiếp (nhỏ hơn hoặc bằng ) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.
d) Góc nội tiếp chắn nửa đường tròn là góc vuông.
2. Các dạng toán thường gặp
Dạng 1: Chứng minh các tam giác đồng dạng, hệ thức về cạnh, hai góc bằng nhau, các đoạn thẳng bằng nhau
Phương pháp:
Ta thường sử dụng hệ quả
Trong một đường tròn:
a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
c) Góc nội tiếp (nhỏ hơn hoặc bằng ) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.
d) Góc nội tiếp chắn nửa đường tròn là góc vuông.
Dạng 2: Chứng minh hai đường thẳng vuông góc, song song. Tính độ dài, diện tích
Phương pháp:
Ta sử dụng hệ quả để suy ra các góc bằng nhau từ đó chứng minh theo yêu cầu bài toán.