Toptailieu.vn giới thiệu Giải VBT Toán lớp 9 Bài 3. Góc nội tiếp trang 94,95,96,97 chi tiết giúp học sinh xem và so sánh lời giải từ đó biết cách làm bài tập trong VBT Toán 9. Mời các bạn đón xem:
VBT Toán lớp 9 Bài 3. Góc nội tiếp
Phần câu hỏi bài 3 trang 94 Vở bài tập toán 9 tập 2
Câu 7.
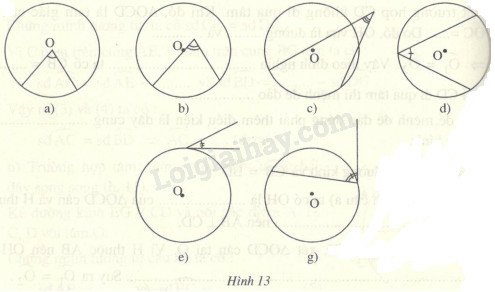
Khoanh tròn vào chữ cái dưới hình chỉ góc nội tiếp ở hình 13:
Phương pháp giải:
Sử dụng định nghĩa góc nội tiếp : “Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó”.
Trả lời:
Theo định nghĩa ta thấy chỉ có hình d thỏa mãn.
Chọn D.
Câu 8.
Trên đường tròn lần lượt đặt ba cung có số đo là Số đo của góc ACB là:
Khoanh tròn vào chữ cái trước kết quả đúng.
Phương pháp giải:
Sử dụng “ số đo của cả đường tròn là ” để tìm , từ đó tính số đo cung
Sử dụng số đo góc nội tiếp bằng nửa số đo cung bị chắn để tính góc
Trả lời:
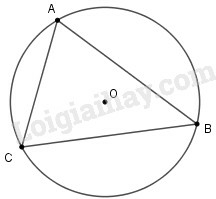
Ta có sđ + sđ + sđ
Suy ra sđ
Nhận thấy là góc nội tiếp chắn cung nên sđ
.
Chọn C
Xem hình 14 (hai đường tròn có tâm là B, C và điểm B nằm trên đường tròn tâm C).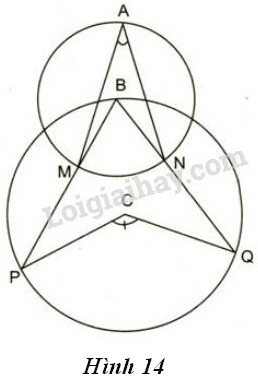
a) Biết , tính
b) Nếu thì có số đo bằng bao nhiêu ?
Phương pháp giải:
Ta sử dụng các kiến thức sau:
Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
Góc nội tiếp (nhỏ hơn hoặc bằng ) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung.
Trả lời:
a) Vì và nằm trên đường tròn tâm nên góc ở tâm
Và nằm trên đường tròn tâm nên góc ở tâm
b) Nếu thì ta có :
và
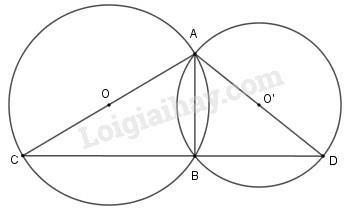
Cho đường tròn tâm , đường kính và là một điểm nằm bên ngoài đường tròn. và lần lượt cắt đường tròn tại và . Gọi là giao điểm của và . Chứng minh rằng vuông góc với .
Phương pháp giải:
Sử dụng góc nội tiếp chắn nửa đường tròn là góc vuông để chỉ ra các đường cao của tam giác
Sử dụng tính chất trực tâm để suy ra
Trả lời:
Vì nằm trên đường tròn tâm nên ( góc nội tiếp chắn nửa đường tròn)
Suy ra và
Do đó, là hai đường cao của và là giao điểm của và
Vậy vì là trực tâm của tam giác
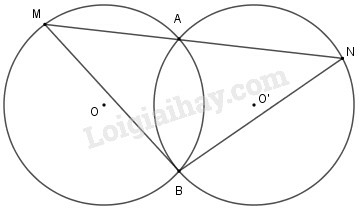
Cho hai đường tròn và cắt nhau tại và . Vẽ các đường kính và của hai đường tròn. Chứng minh rằng ba điểm thẳng hàng.
Phương pháp giải:
Sử dụng góc nội tiếp chắn nửa đường tròn là góc vuông.
Từ đó chứng minh
Trả lời:
Nối Xét các góc nội tiếp :
Với đường tròn ta có
Vì là góc nội tiếp chắn nửa đường tròn.
Với đường tròn ta có
Vì là góc nội tiếp chắn nửa đường tròn.
Vậy ba điểm thẳng hàng.
Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại A và B. Vẽ đường thẳng qua A cắt (O) tại M và cắt (O') tại N (A nằm giữa M và N). Hỏi BMN là tam giác gì ? Tại sao ?
Phương pháp giải:
Sử dụng các góc nội tiếp chắn các cung bằng nhau thì bằng nhau để chỉ ra các góc bằng nhau
Trả lời:
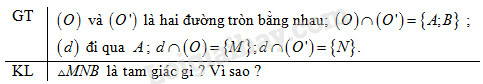
Từ giả thiết ta có cung của và bằng nhau vì hai góc nội tiếp chắn các cung bằng nhau thì bằng nhau.
Vậy là tam giác cân tại
Bài 14 trang 96 Vở bài tập toán 9 tập 2
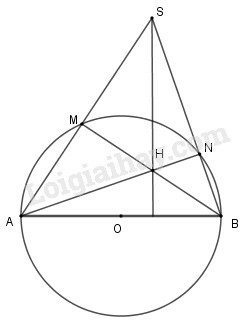
Trên đường tròn đường kính , lấy điểm (khác và ). vẽ tiếp tuyến của tại . Đừờng thẳng cắt tiếp tuyến đó tại . Chứng minh rằng ta luôn có
Phương pháp giải:
+ Sử dụng góc nội tiếp chắn nửa đường tròn là góc vuông.
+ Chứng minh đồng dạng với từ đó suy ra tỉ lệ cạnh để có đẳng thức cần chứng minh.
Trả lời:
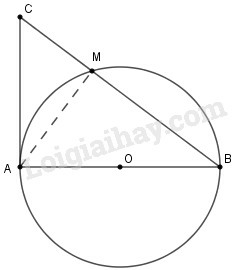
Nối
Xét và
Ta có vì góc nội tiếp chắn nửa đường tròn
Và vì (vì tam giác vuông tại ) và (do )
Hai tam giác vuông có góc nhọn bằng nhau nên ta có :
Cho đường tròn và một điểm cố định không nằm trên đường tròn. Qua kẻ hai đường thẳng. Đường thẳng thứ nhất cắt tại và . Đường thẳng thứ hai cắt tại và . Chứng minh
Phương pháp giải:
Sử dụng hai góc nội tiếp cùng chắn một cung thì bằng nhau
Chứng minh các tam giác đồng dạng từ đó suy ra tỉ lệ cạnh và hệ thức cần chứng minh.
Trả lời:
a) M nằm bên trong đường tròn
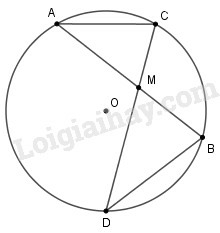
Xét và , ta có:
(hai góc đối đỉnh)
vì cùng chắn cung
Theo tính chất hai tam giác đồng dạng ta có :
b) nằm bên ngoài đường tròn
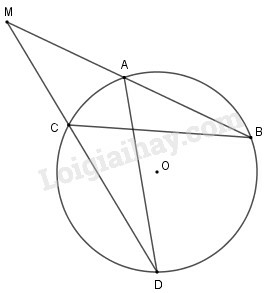
Xét đường tròn có (hai góc nội tếp cùng chắn cung )
Xét và , ta có:
Góc là góc chung
vì cùng chắn cung
Theo tính chất của hai tam giác đồng dạng suy ra :
Cho là ba dây của đường tròn . Từ điểm chính giữa của cung vẽ dây song song với dây . Gọi giao điểm của và là . Chứng minh và .
Phương pháp giải:
Ta sử dụng các kiến thức sau:
+ Các góc nội tiếp bằng nhau chắn các cung bằng nhau.
+ Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau.
Từ đó chỉ ra các góc bằng nhau để có tam giác cân, suy ra các cặp cạnh bằng nhau.
Trả lời:
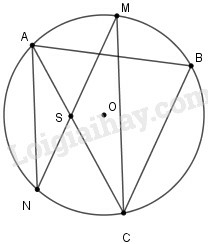
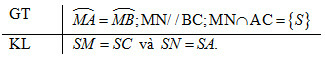
Từ giả thiết ta có
Mà vì
Do đó ta có hay cân tại
Từ ta có (các góc nội tiếp chắn hai cung bằng nhau thì bằng nhau)
Hay là tam giác cân tại (tính chất).
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
2021 © All Rights Reserved.