Toptailieu.vn giới thiệu Giải bài tập Toán 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn chính xác, chi tiết nhất giúp học sinh dễ dàng làm bài tập Căn bậc hai lớp 9.
Giải bài tập Toán 9 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
Trả lời câu hỏi giữa bài:
Trả lời câu hỏi 1 trang 81 Toán 9 Tập 2: Hãy chứng minh định lý trên.
Phương pháp giải:
Sử dụng:
+ Số đo góc nội tiếp bằng nửa số đo cung bị chắn
+ Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.
Lời giải:
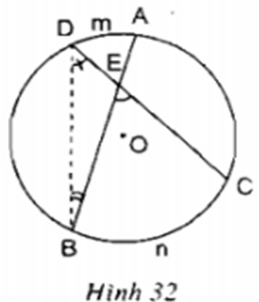
Xét đường tròn có
(góc nội tiếp chắn cung )
(góc nội tiếp chắn cung )
Mà (góc ngoài của tam giác BDE)
Do đó
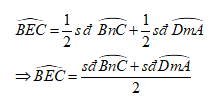
Trả lời câu hỏi 2 trang 82 Toán 9 Tập 2: Chứng minh định lý:
"Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn."
Phương pháp giải:
Sử dụng:
+ Số đo góc nội tiếp bằng nửa số đo cung bị chắn
+ Góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.
Lời giải:
Xét đường tròn (O)
Trường hợp 1:
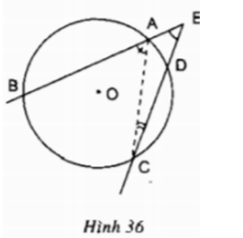
Ta có: là góc ngoài của tam giác AEC.
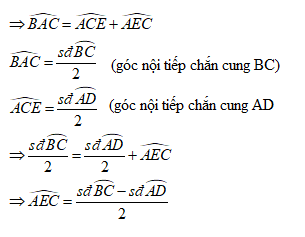
Trường hợp 2:
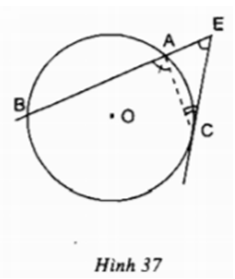
Ta có: là góc ngoài của tam giác AEC
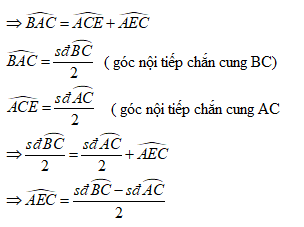
Trường hợp 3:
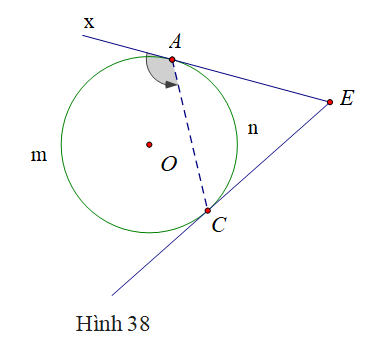
Ta có: là góc ngoài của tam giác AEC
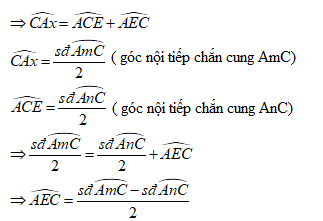
Bài tập trang 82 - 83 SGK Toán 9
Bài 36 trang 82 sgk Toán lớp 9 tập 2: Cho đường tròn và hai dây , . Gọi lần lượt là điểm chính giữa của cung và cung . Đường thẳng cắt dây tại và cắt dây tại . Chứng minh rằng tam giác là tam giác cân.
Phương pháp giải:
+) Sử dụng: "Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn."
Lời giải:
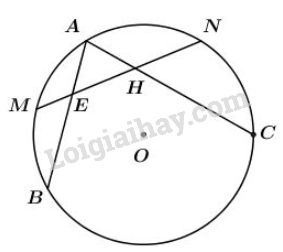
Xét đường tròn (O):
Vì là góc có đỉnh bên trong đường tròn chắn các cung và cung nên =
Vì là góc có đỉnh bên trong đường tròn chắn các cung và cung nên =
Ta có:
( là điểm chính giữa cung ).
là điểm chính giữa cung ).
Từ (1),(2), (3), (4), suy ra . Do đó cân tại A
Bài 37 trang 82 sgk Toán lớp 9 tập 2: Cho đường tròn và hai dây , bằng nhau. Trên cung nhỏ lấy một điểm . Gọi là giao điểm của và . Chứng minh:
Phương pháp giải:
+) Góc có đỉnh nằm ngoài đường tròn có số đo bằng nửa hiệu số đo hai cung bị chắn.
Lời giải:
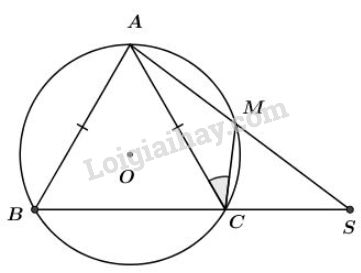
Xét đường tròn , ta có:
là góc có đỉnh ở ngoài đường tròn chắn cung và
(1)
và = (2) (góc nội tiếp chắn cung )
Theo giả thiết thì: (hai dây bằng nhau căng hai cung bằng nhau).
(3)
Từ (1), (2), (3) suy ra: (đpcm)
Bài 38 trang 82 sgk Toán lớp 9 tập 2: Trên một đường tròn, lấy liên tiếp ba cung sao cho
. Hai đường thẳng và cắt nhau tại . Hai tiếp tuyến của đường tròn tại và cắt nhau tại . Chứng minh rằng:
a) ;
b) là phân giác của
Phương pháp giải:
+) Góc có đỉnh nằm ngoài đường tròn có số đo bằng nửa hiệu số đo hai cung bị chắn.
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+) Số đo góc nội tếp bằng nửa số đo cung bị chắn
Lời giải:
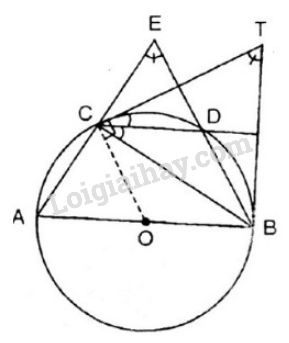
a) Xét đường tròn có nên
Ta có là góc có đỉnh ở bên ngoài đường tròn chắn cung và nên:
và cũng là góc có đỉnh ở bên ngoài đường tròn chắn cung lớn và nhỏ (hai cạnh đều là tiếp tuyến của đường tròn) nên:
Vậy
b) Xét đường tròn có:
là góc tạo bởi tiếp tuyến và dây cung chắn cung nên:
là góc nội tiếp chắn cung nên:
Vậy . hay là phân giác của
Bài 39 trang 83 sgk Toán lớp 9 tập 2: Cho và là hai đường kính vuông góc của đường tròn . Trên cung nhỏ lấy một điểm . Tiếp tuyến tại cắt tia ở , đoạn thẳng cắt ở . Chứng minh .
Phương pháp giải:
+) Góc có đỉnh nằm ngoài đường tròn có số đo bằng nửa hiệu số đo hai cung bị chắn.
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Lời giải:
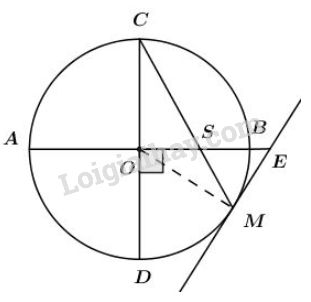
Xét đường tròn có hai đường kính nên nên (1)
+) Ta có là góc có đỉnh nằm trong đường tròn chắn cung và cung
(2)
+) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung
(3)
Từ (1), (2), (3) ta có: nên cân tại và (đpcm).
Bài 40 trang 83 sgk Toán lớp 9 tập 2: Qua điểm nằm bên ngoài đường tròn , vẽ tiếp tuyến và cát tuyến của đường tròn. Tia phân giác của cắt dây tại Chứng minh
Phương pháp giải:
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+) Số đo của góc tạo bởi tiếp tuyến của dây cung bằng nửa số đo cung bị chắn.
+) 2 góc nội tiếp bằng nhau chắn 2 cung bằng nhau.
Lời giải:
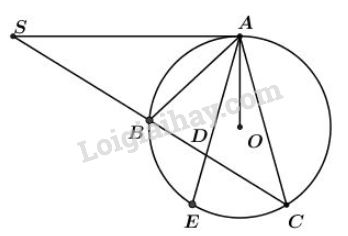
Gọi là giao điểm thứ hai của với đường tròn
Xét đường tròn ta có:
+) là góc có đỉnh nằm trong đường tròn chắn cung và
(1)
+) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung
(2)
+) Có: (do là phân giác góc )
(hai góc nội tiếp bằng nhau chắn hai cung bằng nhau).
(3)
Từ (1) và (3) (4)
Từ (2) và (4) tam giác cân tại hay .
Bài 41 trang 83 sgk Toán lớp 9 tập 2: Qua điểm nằm bên ngoài đường tròn vẽ hai cát tuyến và sao cho hai đường thẳng và cắt nhau tại một điểm nằm bên trong đường tròn.
Chứng minh:
Phương pháp giải:
+) Góc có đỉnh nằm ngoài đường tròn có số đo bằng nửa hiệu số đo hai cung bị chắn.
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+) Số đo của góc nội tiếp bằng nửa số đo cung bị chắn.
Lời giải:
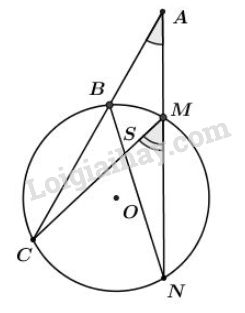
Xét đường tròn có:
+) là góc có đỉnh nằm ngoài đường tròn chắn cung và (1)
+) là góc có đỉnh nằm trong đường tròn chắn cung và (2)
Cộng (1) và (2) theo vế với vế:
+ (3)
Mà là góc nội tiếp chắn cung
. (4)
Từ (3) và (4) ta được: (đpcm).
Bài 42 trang 83 sgk Toán lớp 9 tập 2: Cho tam giác nội tiếp đường tròn. theo thứ tự là các điểm chính giữa các cung bị chắn bởi các góc .
a) Chứng minh
b) cắt tại . Chứng minh tam giác là tam giác cân.
Phương pháp giải:
+) Góc có đỉnh nằm ngoài đường tròn có số đo bằng nửa hiệu số đo hai cung bị chắn.
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Lời giải:
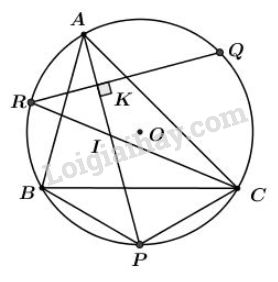
a) Gọi giao điểm của và là .
Vì theo thứ tự là các điểm chính giữa các cung bị chắn bởi các góc nên , ,
Suy ra
Xét đường tròn ta có:
+) là góc có đỉnh ở bên trong đường tròn chắn cung và nên:
Vậy hay
b) Xét đường tròn ta có:
+) là góc có đỉnh ở bên trong đường tròn chắn cung và nên: (1)
+) góc nội tiếp chắn cung , nên (2)
Theo giả thiết thì (3)
và (4)
Từ (1), (2), (3), (4) suy ra: . Do đó cân.
Bài 43 trang 83 sgk Toán lớp 9 tập 2: Cho đường tròn và hai dây cung song song ( và nằm trong cùng một nửa mặt phẳng bờ ); cắt tại . Chứng minh
Phương pháp giải:
+) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+) Hai cung bị chắn giữa hai dây song song thì bằng nhau
Lời giải:
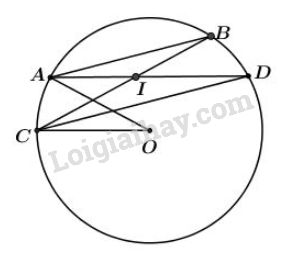
Vì nên ( 2 cung chắn giữa 2 dây song song thì bằng nhau) (1)
Ta có: là góc có đỉnh ở trong đường tròn chắn cung và cung
Theo (1) suy ra (3)
Mà (góc ở tâm chắn cung ) (4)
Từ (3), (4), ta có (đpcm).
Lý thuyết Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn
1. Các kiến thức cần nhớ
a. Góc có đỉnh bên trong đường tròn
Định nghĩa: Trong hình , góc nằm trong đường tròn được gọi là góc có đỉnh ở bên trong đường tròn.
Định lý: Số đo của góc đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
Ví dụ: Trong hình , .
b. Góc có đỉnh bên ngoài đường tròn
Định nghĩa: Góc có đỉnh nằm bên ngoài đường tròn và các cạnh đều có điểm chung với đường tròn (hình ) là góc có đỉnh bên ngoài đường tròn.
Định lý: Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
Ví dụ: Trong hình ,
Trong hình ,
Trong hình ,
2. Các dạng toán thường gặp
Dạng 1: Chứng minh hai góc hoặc hai đoạn thẳng bằng nhau. Tính góc và độ dài đoạn thẳng
Phương pháp:
+ Ta thường sử dụng các kiến thức về số đo của góc có đỉnh bên trong và bên ngoài đường tròn, góc nội tiếp, góc tạo bởi tiếp tuyến và dây cung để chứng minh các góc bằng nhau
+ Sử dụng định lý Pytago, hệ thức lượng trong tam giác vuông để tính toán.
Dạng 2: Chứng minh hai đường thẳng song song, hai đường thẳng vuông góc, chứng minh các hệ thức.
Phương pháp:
+ Ta thường sử dụng các kiến thức về số đo của góc có đỉnh bên trong và bên ngoài đường tròn, góc nội tiếp, góc tạo bởi tiếp tuyến và dây cung để chứng minh các góc bằng nhau
+) Sử dụng quan hệ từ vuông góc đến song song.

